
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дроби обыкновенные и десятичныеСодержание книги Поиск на нашем сайте
Одна или несколько равных частей единицы называются обыкновенной дробью. Записывается с помощью черты и двух натуральных чисел. Число, стоящее под чертой и показывающее, на сколько равных частей разделена единица, называется знаменателем дроби. Число, стоящее над чертой и показывающее, сколько взято таких равных частей, называется числителем дроби. Дробную черту можно рассматривать как знак деления: Дробь, у которой числитель равен знаменателю, равна единице: Дробь, в которой числитель меньше знаменателя, называется правильной: Дробь, в которой числитель равен знаменателю или больше его, называется неправильной: Дроби Основное свойство дроби. Если оба члена дроби увеличить в одно и то же число раз или уменьшить в одно и то же число раз, то величина дроби не изменится. Обыкновенную дробь, знаменатель которой равен 10,100,1000 и т.д. называют десятичной дробью:
Периодические дроби Бесконечная десятичная дробь, в которой, начиная с некоторого разряда, цифры повторяются, называется периодической: 0,3333…=0,(3); 2,6555…=2,6(5). Любую обыкновенную дробь можно записать в виде либо конечной десятичной дроби, либо бесконечной периодической дроби. Правило перевода бесконечной периодической дроби в обыкновенную. Надо из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и записать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, а после девяток дописать столько нулей, сколько цифр между запятой и первым периодом. Например: Правило перевода обыкновенной дроби в бесконечную периодическую дробь. Чтобы обратить обыкновенную дробь в десятичную, следует разделить числитель на знаменатель по правилу деления десятичной дроби на целое число. Например:
Отношение. Проценты. Пропорции Отношением числа x к числу y называется частное чисел x и y, то есть Пропорцией называется равенство двух отношений, то есть а и y называются крайними членами, x и b называются средними членами пропорции. Свойства пропорции. · произведение крайних членов пропорции равно произведению её средних членов, то есть если · обратно: числа a,b,x,y составляют пропорцию · из пропорции · чтобы найти неизвестный средний (крайний) член пропорции, надо произведение крайних (средних) членов разделить на известный средний (крайний) член пропорции
Процентом называется сотая часть какого-либо числа. Процент обозначается знаком %. Чтобы число процентов выразить в виде дроби, достаточно число процентов разделить на сто. Например: 125%=1,25; 2,3%=0,023. Нахождение процентов данного числа. Чтобы найти а% от числа b, надо b умножить на а и разделить на 100. Например: 30% от 60 составляют Нахождение числа по его процентам. Чтобы найти процентное отношение двух чисел a и b, надо отношение чисел умножить на 100%, то есть Например: при плановом задании 60 автомобилей в день завод выпускает 66 автомобилей. На сколько процентов выполнен план? Решение:
Целые числа Два числа, отличающиеся друг от друга только знаком, называются противоположными числами: 1 и -1, 2 и -2, 15 и -15,… Числа натуральные, им противоположные, а так же число нуль составляют множество целых чисел Z. Множество натуральных чисел, дополненное нулем, называется множеством целых неотрицательных чисел. Для целых чисел определены действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, причем сложение, вычитание и умножение выполняются всегда.
Рациональные числа Объединение множеств целых и дробных чисел (положительных и отрицательных) составляет множество рациональных чисел Q. Любое рациональное число На множестве рациональных чисел можно производить действия сложения, вычитания, умножения, деления (кроме деления на нуль).
Иррациональные числа Иррациональным числом называют бесконечную десятичную непериодическую дробь. Множество таких дробей составляет множество иррациональных чисел I. Например: 0,131331333125…; π ≈ 3,14; e ≈ 2,7;
Действительные числа Объединение множества рациональных чисел и множества иррациональных чисел даёт множество действительных чисел, которое обозначается R.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.236.101 (0.006 с.) |

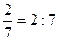

 .
. .
. и
и  называются равными, если
называются равными, если  .
.
 .
.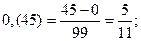
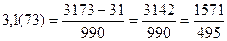 .
.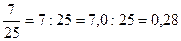 .
. или х: у. Отношение
или х: у. Отношение  .
. .
. вытекают пропорции
вытекают пропорции  , то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.
, то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно. ;
; .
. 
 .
. .
. .
.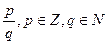 может быть представлено в виде конечной или бесконечной периодической десятичной дроби.
может быть представлено в виде конечной или бесконечной периодической десятичной дроби. и т.д.
и т.д.


