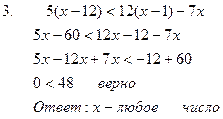Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратные уравнения. Теорема ВиетаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Уравнение вида а – первый коэффициент; b – второй коэффициент; с – свободный член. Квадратные уравнения, в которых хотя бы один из коэффициентов b или с равен нулю, называются неполными.
Выведем формулу корней квадратного уравнения. Для этого решим уравнение Выделим полный квадрат: Тогда уравнение (2) примет вид или Число корней зависит от знака дроби
При решении квадратного уравнения, в котором второй коэффициент b – четное число, используют следующую формулу:
Квадратное уравнение, первый коэффициент которого равен 1, называется приведенным:
Теорема Виета: Сумма корней квадратного уравнения Доказательство:
Теорема доказана. Следствие: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену: Обратная теорема: Если числа x1 и x2 такие, что
Определение знаков корней квадратного уравнения.
Уравнение 4-ой степени вида Разложение квадратного трехчлена на множители Квадратным трехчленом называется многочлен вида x – переменная, a, b, c – числа, причем а ≠ 0. Корнем квадратного трехчлена называется значение переменной, при котором значение этого трехчлена равно нулю. Квадратный трехчлен имеет те же корни, что и квадратное уравнение Теорема: Если x1 и x2 – корни квадратного трехчлена Доказательство:
Если квадратный трехчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.
Уравнения с несколькими неизвестными. Системы уравнений Уравнение вида f(x; y)=0 называется уравнением с двумя переменными. Решением уравнения с двумя переменными называется пара значений переменных, обращающих уравнение в верное равенство. Обычно решение записывают в виде пары чисел (x0; y0). Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное числовое равенство. Уравнение вида Если ставится задача найти все общие решения двух уравнений с двумя переменными, то говорят, что надо решить систему уравнений. Решением системы уравнений с двумя переменными называется пара значений переменных, удовлетворяющих каждому из уравнений. Решить систему уравнений – значит найти все ее решения или установить, что их нет. Две системы уравнений называют равносильными, если они имеют одни и те же решения. Система линейных уравнений с двумя переменными имеет вид Не решая систему линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных. 1. Если 2. Если 3. Если Методы решения систем уравнений: 1. Метод подстановки. 2. Метод алгебраического сложения. 3. Графический метод. 4. Метод введения новых переменных.
Неравенства и их свойства Запись, в которой два числа или два выражения, содержащие переменные, соединены знаком >, <, ≥, ≤ называется неравенством. Неравенства, составленные с помощью знаков >, < называются строгими; неравенства, составленные с помощью знаков≥, ≤, называются нестрогими. Два неравенства вида a > b и c > d называются неравенствами одинакового смысла; а вида a > b, c < d неравенствами противоположного смысла. Вместо двух неравенств x < a, a < y используется запись x < a < y – двойное неравенство. Неравенства, содержащие только числа, называются числовыми неравенствами. Решить неравенство, содержащее переменную, это значит найти множество значений переменной, при котором это неравенство является верным. Элементы этого множества называются решением неравенства. Два неравенства называются равносильными, если множества их решений совпадают. Свойства: 1. Если a > b, то b < a. 2. Если a > b и b > c, то a > c. 3. Если к обеим частям верного неравенства прибавить одно и то же число, то получим верное неравенство: a > b => a + c > b + c. 4. Если из одной части верного неравенства перенести в другую какое-либо слагаемое, переменив его знак на противоположный, то получим верное неравенство: a + b > c => a – c > -b. 5. Если обе части верного неравенства умножить на одно и то же положительное число, то получим верное неравенство: a > b, n > 0 => na > nb ( 6. Если обе части верного неравенства умножить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получим верное неравенство: a > b, n < 0 => na < nb ( 7. Неравенства одного смысла можно почленно складывать: a > b, c > d =>a + c > b + d 8. Неравенства противоположного смысла можно почленно вычитать: a > b, c < d => a - c > b - d 9. Если a > b > 0, c > d > 0 => ac > bd. 10. Обе части неравенства можно возводить в одну и ту же натуральную степень: a > b > 0, m 11. Из каждой части неравенства можно извлекать корень одной и той же натуральной степени: a > b > 0, m
Решение линейных неравенств Линейным неравенством называется неравенство вида Если a>0, то неравенство Если a<0, то неравенство
Например:
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.01 с.) |

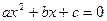 , где x – переменная, a, b, c – некоторые числа, причем, а ≠ 0, называется квадратным.
, где x – переменная, a, b, c – некоторые числа, причем, а ≠ 0, называется квадратным.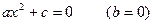
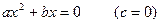
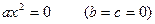
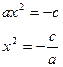 1) Если ас > 0 – корней нет
2) Если ac < 0
1) Если ас > 0 – корней нет
2) Если ac < 0 
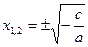
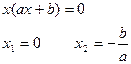
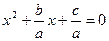 (2).
(2).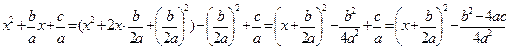 .
.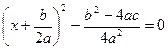
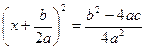 (3).
(3).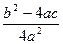 , т.к. а ≠ 0, то
, т.к. а ≠ 0, то 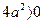
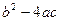 . Обозначим его D =
. Обозначим его D = 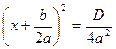 (4). Рассмотрим случаи:
(4). Рассмотрим случаи: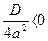 , но
, но
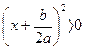 для любого действительного x.
Значит, корней нет.
для любого действительного x.
Значит, корней нет.
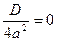
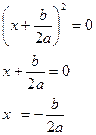 Значит, два равных корня
Значит, два равных корня 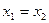 .
.
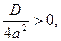 то
то 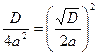
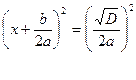
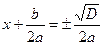
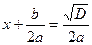 или
или 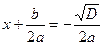
 или
или 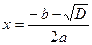 Значит, два различных корня
Значит, два различных корня 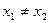
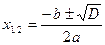 , где
D =
, где
D = 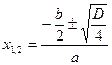 , где
, где 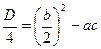 .
.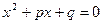 . Корни приведенного квадратного уравнения можно найти по формулам:
. Корни приведенного квадратного уравнения можно найти по формулам: 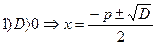 ;
;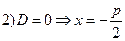 .
. , произведение корней равно
, произведение корней равно 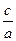 .
.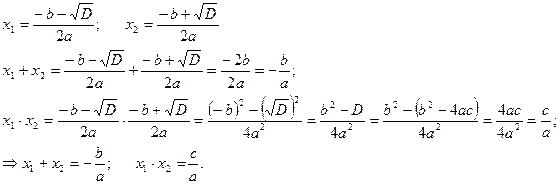
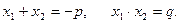
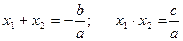 , то они являются корнями квадратного уравнения
, то они являются корнями квадратного уравнения 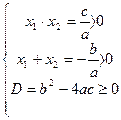
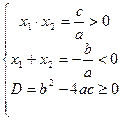
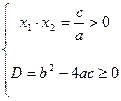
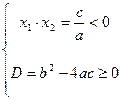
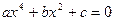 , где а ≠ 0, называется биквадратным.
, где а ≠ 0, называется биквадратным.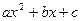 , где
, где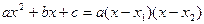 .
.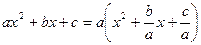 . По теореме Виета
. По теореме Виета 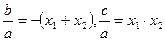
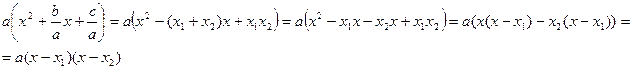 Теорема доказана.
Теорема доказана.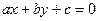 , где x, y – переменные, a, b, c – действительные числа, называется линейным.
, где x, y – переменные, a, b, c – действительные числа, называется линейным.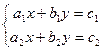 .
.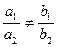 , т.е. коэффициенты при x и y не пропорциональны, то система имеет одно решение. Графически – прямые пересекаются.
, т.е. коэффициенты при x и y не пропорциональны, то система имеет одно решение. Графически – прямые пересекаются.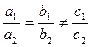 , т.е. коэффициенты при x и y пропорциональны, а свободные члены нет, то система не имеет решений. Графически – прямые параллельны.
, т.е. коэффициенты при x и y пропорциональны, а свободные члены нет, то система не имеет решений. Графически – прямые параллельны.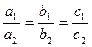 , т.е. все коэффициенты пропорциональны, то система имеет множество решений. Графически – прямые совпадают.
, т.е. все коэффициенты пропорциональны, то система имеет множество решений. Графически – прямые совпадают.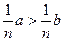 ).
). ).
).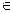 N => am > bm.
N => am > bm.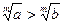 .
.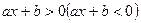 .
.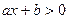 равносильно неравенству
равносильно неравенству 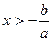 .
.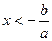 .
.