
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение квадратных неравенствСодержание книги Поиск на нашем сайте
Квадратным неравенством называется неравенство вида Решение неравенства такого типа можно рассматривать как нахождение промежутков, в которых квадратичная функция С помощью графика квадратного трехчлена можно указать те значения х, при которых будет выполняться нужное неравенство
Квадратные неравенства можно решать методом интервалов.
Решение рациональных неравенств методом промежутков Неравенство имеет вид Решение рациональных неравенств методом промежутков (методом интервалов) основано на следующем свойстве функций вида Для нахождения таких промежутков знакопостоянства функции Изменение знаков функции f(x) удобно иллюстрировать с помощью волнообразной кривой, которую чертят справа налево. На тех промежутках, где кривая проходит выше координатной прямой, выполняется неравенство f(x)>0; на тех промежутках, где кривая проходит ниже, – неравенство f(x)<0.
Понятие функции, график функции, область определения, множество значений Зависимость переменной y от переменной х называется функцией, если каждому значению х соответствует единственное значение у. При этом используют запись: y=f(x). Переменную х называют независимой переменной (аргументом); у называют зависимой переменной (функцией). Значение у, соответствующее заданному значению х, называют значением функции. Все значения, которые принимает независимая переменная, образуют область определения функции D(f).
Все значения, которые принимает зависимая переменная, образуют множество значений функции Е(f). Элементы множества D(f) так же называют значениями аргумента, а соответствующие им элементы множества Е(f) - значениями функции. Графиком функции у = f(x) называется множество всех точек (х; у) координатной плоскости, таких, что Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая, параллельная оси Оу, пересекалась с указанным графиком не более чем в одной точке. Способы задания функции: 1. Аналитический – с помощью формулы: у = 5х2 – 7. 2. Табличный – с помощью таблицы:
3. Описательный. 4. Графический – с помощью графика:
Свойства функции 1. Областью определения функции называются все значения переменной х, при которых функция имеет смысл (выполнимы указанные действия). 2. Множеством значений функции называются все значения переменной у. 3. Функция у = f(x) называется четной, если для любого значения х из области определения функции значение – х так же принадлежит области определения (область определения симметрична относительно начала отсчета) и выполняется равенство: f(-x) = f(x). График четной функции симметричен относительно оси ординат (оси Оу). Функция у = f(x) называется нечетной, если для любого значения х из области определения функции значение -х так же принадлежит области определения и выполняется равенство: f(-x) = -f(x). График нечетной функции симметричен относительно начала координат. 4. Нулем функции называется такое значение аргумента х из области определения функции, при котором значение функции равно 0. Для того, чтобы найти нули функции необходимо решить уравнение f(x) = 0. 5. Промежутки, на которых функция либо положительна, либо отрицательна, т.е. имеет один и тот же знак, называются промежутками знакопостоянства. 6. Функция называется периодической, если существует такое число Т ≠ 0, что для любого значения аргумента х из области определения значения х+Т и х–Т так же принадлежат области определения функции и выполняется равенство f(x) = f(x + T) = f(x - T).
7. Функция называется возрастающей на промежутке Х, если для любых х1 и х2 из этого промежутка, таких что х1 < х2, выполняется неравенство f(x1) < f(x2), т.е. большему значению аргумента соответствует большее значение функции. Функция называется убывающей на промежутке Х, если для любых х1 и х2 из этого промежутка, таких что х1 < х2, выполняется неравенство f(x1) > f(x2), т.е. большему значению аргумента соответствует меньшее значение функции. Возрастающая или убывающая на некотором промежутке функция называется монотонной. Промежутки, на которых функциявозрастает или убывает, называются промежутками монотонности. 8. Функция называется ограниченной снизу на некотором множестве Х, если существует такое действительное число М, что для каждого Функция называется ограниченной сверху на некотором множестве Х, если существует такое действительное число М, что для каждого Функция называется ограниченной на некотором множестве Х, если она ограничена и снизу, и сверху. 9. Наибольшим значением функции называется самое большое значение, которое принимает переменная у; наименьшим значением функции называется самое маленькое значение, которое принимает переменная у.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 342; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.220.255 (0.01 с.) |

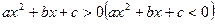 , где
, где  . Возможны так же знаки нестрогих неравенств
. Возможны так же знаки нестрогих неравенств  .
.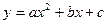 принимает положительные или отрицательные значения.
принимает положительные или отрицательные значения.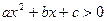 или
или  . Все возможные случаи расположения параболы
. Все возможные случаи расположения параболы 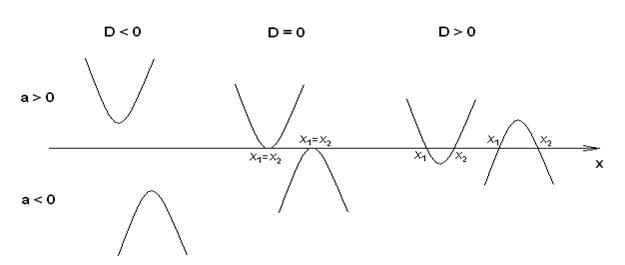
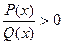 , где P(x) и Q(x) – многочлены. Вместо знака > может быть любой знак неравенства.
, где P(x) и Q(x) – многочлены. Вместо знака > может быть любой знак неравенства.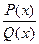 , где P(x) и Q(x) – рациональные выражения: если такая функция обращается в нуль в точках x1 и х2 (х1 < х2) и между этими точками не имеет других нулей или точек разрыва, то в промежутке (х1; х2) функция сохраняет знак.
, где P(x) и Q(x) – рациональные выражения: если такая функция обращается в нуль в точках x1 и х2 (х1 < х2) и между этими точками не имеет других нулей или точек разрыва, то в промежутке (х1; х2) функция сохраняет знак.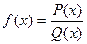 на числовой прямой отмечают все точки, в которых функция обращается в нуль или не существует (терпит разрыв). Эти точки разбивают числовую прямую на несколько промежутков, внутри каждого из которых функция f(x) сохраняет знак. Чтобы определить этот знак, достаточно найти знак функции в какой-либо точке данного промежутка.
на числовой прямой отмечают все точки, в которых функция обращается в нуль или не существует (терпит разрыв). Эти точки разбивают числовую прямую на несколько промежутков, внутри каждого из которых функция f(x) сохраняет знак. Чтобы определить этот знак, достаточно найти знак функции в какой-либо точке данного промежутка.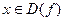 , а у = f(x), причем х называется абсциссой, у – ординатой.
, а у = f(x), причем х называется абсциссой, у – ординатой.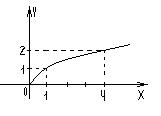
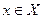 , f(x)
, f(x) 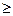 M.
M.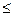 M.
M.


