
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовая прямая, числовые промежуткиСодержание книги Поиск на нашем сайте Прямую линию с выбранными на ней началом отсчёта, единичным отрезком и направлением называют координатной прямой.
Каждому числу можно поставить в соответствие единственную точку на координатной прямой. Для числовых промежутков вводят обозначения: · [a; b] или a≤ х ≤ b – замкнутый промежуток (или отрезок) с началом a и концом b; · (a; b) или a< х <b - открытый промежуток (интервал); · (a; b] или a< х ≤ b; [a; b) или a≤ х < b – полуоткрытые промежутки (полуинтервалы); · [a; + ∞) или х ≥ a; (- ∞; b] или х ≤ b – лучи; · (a; + ∞) или х >a; (- ∞; b) или х < b – открытые лучи; · (- ∞; + ∞) = R – координатная прямая.
Модуль числа Модулем (абсолютной величиной) действительного числа a называется само это число, если a≥ 0, и противоположное число –a, если a< 0. Модуль a обозначается | a |. Итак,
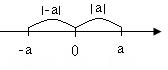
Геометрически | a | означает расстояние на координатной прямой от точки, изображающей число a, до начала отсчёта. Если a≠0, то на координатной прямой существуют две точки a и –a, равноудалённые от нуля, модули которых равны:
Свойства.
Степень с натуральным показателем. Понятие. Свойства Степенью числа a с показателем n, где n Число a называется основанием степени, n – показателем степени. Свойства: · при умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним
· при делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним · при возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним
· степень произведения равна произведению степеней множителей · степень частного равна частному степеней делимого и делителя: · · · если 0 ≤ а < b, то · если а > 1, то · если 0 < а < 1, то · если а < 0, то Утверждения: · чётная степень отрицательного числа есть число положительное; · нечётная степень отрицательного числа есть число отрицательное; · любая степень положительного числа есть число положительное; · при возведении нуля в любую натуральную степень получается нуль; · при возведении 1 в любую натуральную степень получается единица. Степень с целым и дробным (рациональным) показателем. 1. Рассмотрим степень ар, где р Если р=0,то Если р<0, то 2. Рассмотрим степень 3. Степень с целым и рациональным показателем обладает теми же свойствами, что и степень с натуральным показателем:
Квадратный корень и его свойства Квадратным корнем из числа а называется такое число, квадрат которого равен а. Нахождение квадратного корня из числа а называется извлечением квадратного корня. Арифметическим квадратным корнем из числа a (а≥ 0) называется неотрицательное число, квадрат которого равен a. Для арифметического квадратного корня из числа а принято обозначение: Оба равенства для арифметических корней: Свойства: 1. 2. 3.
Числовые выражения Из чисел, знаков действий и скобок можно составить различные числовые выражения: Выполняя указанные в выражении действия, получим число, которое называется числовым значением или значением выражения. Если в выражении встречается деление на нуль, то выражение не имеет смысла. Два выражения называются тождественно равными, если при всех значениях, входящих в них переменных, принадлежащих общей области определений, соответственные значения этих выражений равны.
Одночлены. Многочлены Алгебраическое выражение, представляющее собой произведение чисел переменных и их степеней, называется одночленом: 3ax4; -2b; 0,5c3(-3b2). Стандартным видом одночлена называется произведение, составленное из числового множителя (коэффициента) и степеней различных переменных: -2; а; 53; -9а5х3. Степенью одночлена стандартного вида называется сумма показателей степеней переменных. Например: 8х3у5 – степень одночлена равна 3+5=8; число 7 имеет нулевую степень, т.к. 7=7х0. Одночлены, отличающиеся только числовым коэффициентом или равные между собой, называются подобными. Сумму подобных членов можно заменить одним членом, сложив их коэффициенты и оставив ту же буквенную часть. Такое тождественное преобразование многочленов называют приведение подобных членов. Алгебраическая сумма одночленов называется многочленом. Например: 2а2-3ах5-6 – многочлен;
Если в многочлене все одночлены записаны в стандартном виде и приведены подобные члены, то полученный многочлен называется многочленом стандартного вида: 2х3у3+1,8ху4-3у+7. Степенью многочлена стандартного вида называется наибольшая степень одночлена, входящего в этот многочлен. Степень многочлена стандартного вида, рассмотренного ранее равна 3+3=6.
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 470; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.008 с.) |


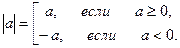
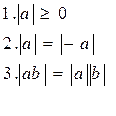

 N, а
N, а 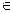 R, называется произведение n множителей, каждый из которых равен a:
R, называется произведение n множителей, каждый из которых равен a:  .
.







 , при m > n.
, при m > n. при m > n.
при m > n.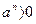 при четном n и
при четном n и  при нечетном n.
при нечетном n. при
при 
 при
при  , где
, где  - рациональное число. Выражение
- рациональное число. Выражение  .
. ;
; ;
; ;
; ;
; .
. . Знак
. Знак  называют знаком арифметического квадратного корня, а число а - подкоренным выражением.
называют знаком арифметического квадратного корня, а число а - подкоренным выражением. при
при  и
и  при
при  можно объединить в одно:
можно объединить в одно:  при любом действительном а.
при любом действительном а. .
. .
. .
.
 - не многочлен.
- не многочлен.


