Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции. Графики основных элементарных функций.Содержание книги
Поиск на нашем сайте Пусть задано числовое множество Если каждому числу Множество Множество, состоящее из всех элементов Число Для того чтобы задать функцию 1) ее область определения 2) указать правило Область определения иногда еще называют областью допустимых значений функции (ОДЗ). Для нахождения ОДЗ функции нужно проанализировать данное соответствие и установить встречающиеся запретные операции (деление на нуль, возведение в рациональную степень отрицательного числа, логарифмические операции над отрицательными числами и т. п.). Функции Если же значения этих функций совпадают лишь на некотором множестве Пусть функции Пусть функции Способы задания функции. Функции могут задаваться различными способами: 1. Самый распространенный из них – аналитический, когда числовая функция задается при помощи формулы. Например: 2. Функция может быть задана различными формулами на разных промежутках. Например: 3. Функции могут задаваться при помощи графиков. Определение. Графиком функции Число Графики элементарных функций. Линейная функция. Функция График линейной функции является прямой. Свойства линейной функции: 1). Область определения функции: 2). Область значений: 3). Линейная функция не является ни четной, ни нечетной.
Квадратичная функция Квадратичной называется функция вида График функции Свойства квадратичной функции: 1). Область определения функции: 2). Область значений: 3). Координаты вершины параболы 4). Если 5). Прямая Пример квадратичной функции
Гипербола Функция вида График функции Свойства функции обратной пропорциональности: 1). Область определения функции: 2). Область значений: 3). Функция нечетна. 4). Функция не пересекает координатные оси. 5). При 6). Функция убывает на промежутках 7). Прямые
|
|||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 518; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 .
. поставлено в соответствие единственное число
поставлено в соответствие единственное число 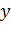 , то говорят, что на множестве
, то говорят, что на множестве  задана числовая функция:
задана числовая функция: 
 называется областью определения функции и обозначается
называется областью определения функции и обозначается  .
.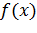 , где
, где  .
.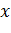 часто называют аргументом функции или независимой переменной, а число
часто называют аргументом функции или независимой переменной, а число 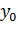 , соответствующее значению
, соответствующее значению  , называют значением функции в точке
, называют значением функции в точке  и обозначают
и обозначают  .
. , нужно указать:
, нужно указать: , по которому каждому значению
, по которому каждому значению  .
. называются равными, если они имеют одну и ту же область определения D и для каждого
называются равными, если они имеют одну и ту же область определения D и для каждого  ,
,  .
. и
и 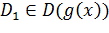 , то говорят, что функции равны на множестве
, то говорят, что функции равны на множестве  .
. определены на одном и том же множестве
определены на одном и том же множестве  , называется суммой функций
, называется суммой функций  . Точно так же определяются разность
. Точно так же определяются разность  , произведение
, произведение  и частное
и частное  двух функций (частное определено на множестве
двух функций (частное определено на множестве  ).
).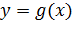 и
и  определены на множествах
определены на множествах  соответственно, причем множество значений функции
соответственно, причем множество значений функции  , называется сложной функций или суперпозицией функций
, называется сложной функций или суперпозицией функций 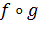 . Важно отметить, что в общем случае суперпозиция
. Важно отметить, что в общем случае суперпозиция 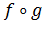 не совпадает с
не совпадает с  .
. .
.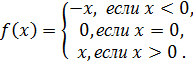
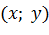 , для которых выполняется равенство
, для которых выполняется равенство 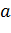 называется нулем функции
называется нулем функции  .
.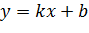 называется линейной функцией.
называется линейной функцией. .
.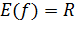 .
.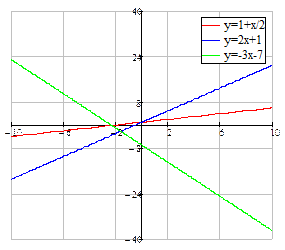 Примеры линейных функций:
Примеры линейных функций: , где
, где 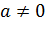 ,
, 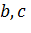 – любые действительные числа.
– любые действительные числа.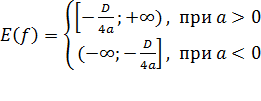 .
.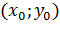 :
: 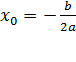 ,
, 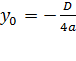 .
.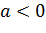 , то ветви параболы направлены вниз. Если
, то ветви параболы направлены вниз. Если 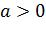 – вверх.
– вверх.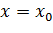 является осью симметрии графика квадратичной функции.
является осью симметрии графика квадратичной функции.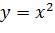 :
: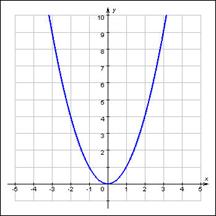
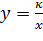 , где
, где 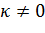 , (
, (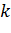 - коэффициент обратной пропорциональности) называется функцией обратной пропорциональности.
- коэффициент обратной пропорциональности) называется функцией обратной пропорциональности.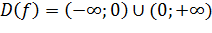 .
.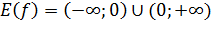 .
.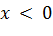
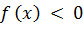 , при
, при 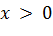
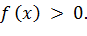
 и
и 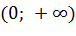 .
. и
и 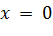 являются асимптотами (при
являются асимптотами (при  и
и 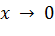 соответственно).
соответственно).