
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комбинаторика. Понятие множества. Перестановки. Размещения. Сочетания.Содержание книги
Поиск на нашем сайте Часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторого действия. Разные пути или варианты, которые приходится выбирать, складываются в самые разнообразные комбинации. Целый раздел математики, называемый комбинаторикой, занят поиском ответов на вопросы: сколько всего есть комбинаций в том или другом случае. Большинство задач комбинаторики можно сформулировать как задачи теории конечных множеств, поэтому эти две темы - элементы теории множеств и комбинаторика- рассматриваются взаимосвязано. Коротко напомним основные понятия теории множеств. Всякая совокупность элементов произвольного рода, обладающая некоторым общим свойством, образует множество (соединение). Можно рассматривать множество всех действительных чисел, множество натуральных чисел, множество всех студентов данного университета, множество парт в данном классе и т.п. Множество считается определенным, если указаны все его элементы или указано их общее свойство. Эти элементы могут быть описаны с помощью некоторого общего признака или просто с помощью некоторого списка, где указаны все элементы. Последний способ возможен лишь в том случае, если множество содержит конечное число элементов; такие множества называются конечными. Характеристикой конечного множества является число его элементов. Множество, состоящее из Всякое конечное множество можно упорядочить. Множества обозначаются большими латинскими буквами, а их элементы — малыми ( Количество элементов конечного множества обозначается N(A). Если каждый элемент множества B принадлежит множеству A, то B называется подмножеством множества A ( Если задано некоторое множество A, то можно рассматривать новое множество M(A) — множество всех его подмножеств. Через Итак, множество является тем, что имеет элементы, а элементы это то, что-либо входит, либо не входит в данное множество. В множестве не может быть двух или более одинаковых элементов, а порядок расположения элементов в множестве не имеет никакого значения. Обозначим некоторое множество символом Над множествами можно выполнять различные операции: объединение ( Объединение множеств Задача 21.1. Решение. Напомним, что в любом множестве все элементы должны быть различны. Другими словами, множество Пересечение множеств Задача 21.2. Решение. В частности, Вычитание из множества Задача 21.3. Пусть Решение. В частности, Если множества Определение. Число различных способов, которыми может быть упорядочено данное множество, состоящее из
Определение. Количество перестановок из
Пусть задано некоторое конечное множество из Определение. Упорядоченная выборка объёма Количество размещений из
Познакомившись с размещением вернемся к понятию перестановки. Определение. Размещение из Другими словами, Определение. Упорядоченная выборка объёма Количество размещений с повторениями вычисляется по формуле
Допустим теперь, что нас не интересует порядок, в котором идут выбранные элементы. Например, нужно из десяти человек выбрать троих дежурных. Такая операция называется неупорядоченной выборкой, или сочетанием, в отличие от упорядоченной выборки – размещения. Определение. Всякая неупорядоченная выборка объёма Количество сочетаний из
Как и в случае с размещениями, существует понятие числа сочетаний с повторениями. Определение. Если из множества, содержащего n элементов, выбирается поочередно m элементов, причём выбранный элемент каждый раз возвращается обратно, то количество способов произвести неупорядоченную выборку называется сочетанием с повторениями и обозначается Количество способов произвести неупорядоченную выборку – число сочетаний с повторениями составляет
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1748; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 элементов, называется упорядоченным, если каждому элементу этого множества поставлено в соответствие натуральное число (номер) от 1 до
элементов, называется упорядоченным, если каждому элементу этого множества поставлено в соответствие натуральное число (номер) от 1 до 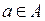 означает, что a есть элемент множества A или элемент a принадлежит множеству A).
означает, что a есть элемент множества A или элемент a принадлежит множеству A). ).
). будем обозначать множество всех подмножеств A, которые имеют k элементов:
будем обозначать множество всех подмножеств A, которые имеют k элементов:  , если
, если  и
и  .
.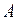 , а все элементы, входящие в это множество, — символами
, а все элементы, входящие в это множество, — символами  . Тогда запись
. Тогда запись  означает, что множество
означает, что множество  ), пересечение (
), пересечение ( ), вычитание (
), вычитание ( ) и пр.
) и пр. есть множество, обозначаемое как
есть множество, обозначаемое как  , которое содержит все элементы множества
, которое содержит все элементы множества  ,
,  . Найдите
. Найдите  .
. .
. , которое содержит все элементы, принадлежащие как множеству
, которое содержит все элементы, принадлежащие как множеству  ).
). .
. .
. . Это множество содержит все элементы множества
. Это множество содержит все элементы множества  ,
,  . Найдите
. Найдите  .
. .
.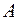 и
и 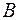 не пересекаются (т. е.
не пересекаются (т. е.  . Множество
. Множество  . Число перестановок из
. Число перестановок из  (21.1.)
(21.1.) одинаковых элементов первого сорта,
одинаковых элементов первого сорта,  одинаковых элементов второго сорта,
одинаковых элементов второго сорта, 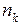 одинаковых элементов k -го сорта, называется количеством перестановок с повторениями, обозначается символом
одинаковых элементов k -го сорта, называется количеством перестановок с повторениями, обозначается символом  . Число перестановок с повторениями вычисляется по формуле
. Число перестановок с повторениями вычисляется по формуле (21.2)
(21.2) различных штук (
различных штук ( ), тогда говорят, что произведена выборка объёма
), тогда говорят, что произведена выборка объёма  .
. элементов по
элементов по 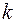 вычисляется следующим образом:
вычисляется следующим образом: (21.3)
(21.3) элементов по
элементов по 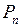 .
.
 .
. (21.4)
(21.4) .
. (21.5)
(21.5) .
. (21.6)
(21.6)


