
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратная матрица. Ранг матрицы.Содержание книги
Поиск на нашем сайте Матрицы. Определители. Основные понятия.
Определение. Матрицей размерности m x n называется прямоугольная таблица вида:
где Числа aij - называются элементами матрицы. Если m=1, а n >1, то матрица является матрицей-строкой. Если m >1, а n=1, то матрица является матрицей-столбцом. Если m=n, то матрица называется квадратной, а число её строк (или столбцов) называется порядком матрицы. Две матрицы A и B называются равными, если их размер одинаков и aij=bij. Нулевая матрица - это матрица, у которой все элементы равны нулю. Единичной матрицей называется квадратная матрица:
Определение. Матрицей транспонированной к матрице A размерности m x n, называется матрица AT размерности n x m, полученная из матрицы A, если её строки записать в столбцы, а столбцы - в строки. Матрицы одинакового размера (однотипные) можно складывать, вычитать, перемножать и умножать на число. Определение. Суммой (разностью) двух однотипных матриц А и В называется матрица С, элементы которой равны сумме или разности
Произведением матрицы A на число p называется матрица, элементы которой равны paij
Произведением двух квадратных матриц A и B называется матрица С, элемент которой, находящийся на пересечении i-ой строки и k-го столбца, является суммой парных произведений элементов i-ой строки первой матрицы на элемент k-ой строки второй матрицы С=АВ.
То же правило распространяется на умножение прямоугольных матриц, у которых число столбцов матрицы-множимого равно числу строк матрицы-множителя. Матрицы для которых АВ=ВА, называются коммутирующими. При умножении двух ненулевых матриц может получиться нулевая матрица. Линейной комбинацией однотипных матриц А1, А2, …, Ак с коэффициентами λ1, λ2, …, λк называется матрица той же размерности А=А1λ1+А2λ2+…+Акλк=0. Определение. Численной характеристикой матрицы первого порядка, то есть определителем первого порядка, называется величина ее элемента a11. Определение. Определителем второго порядка, соответствующим матрице Определение. Определителем третьего порядка, соответствующим матрице Определение. Минор элемента aij - определитель, который получается из исходного, вычеркиванием i -го столбца и j -ой строки.
Определение. Алгебраическим дополнением Aij элемента aij определителя
Определение. Определителем n-го порядка, соответствующим квадратной матрице n-го порядка, называется число, равное сумме парных произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.
Квадратичные формы.
Определение. О днородный многочлен второй степени относительно переменных х1 и х2 Ф(х1, х2) = а 11 не содержащий свободного члена и неизвестных в первой степени, называется квадратичной формой переменных х1 и х2. Определение. Однородный многочлен второй степени относительно переменных х1, х2 и х3
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных х1, х2 и х3.
Рассмотрим квадратичную форму двух переменных. Квадратичная форма имеет симметрическую матрицу А =
Пусть на плоскости задан ортогональный базис Если задана квадратичная форма Ф(х1, х2) = а 11
8. Кривые второго порядка на плоскости (окружность, эллипс, гипербола, парабола).
Определение. Кривой второго порядка называется множество точек, координаты которых удовлетворяют уравнению второго порядка
где Определение. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности. Получим уравнение окружности, если известны ее центр и радиус. Окружность радиуса
Определение. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная. Пусть Пусть сумма расстояний от точки эллипса до фокусов равна где
Рис.8.2. Уравнение (8.2) называется каноническим уравнением эллипса. Определение. Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная. Для получения уравнения гиперболы выберем систему координат. Начало координат расположим на середине отрезка между фокусами, ось
Рис. 8.3. Пусть расстояние между фокусами где Уравнение (8.3) называется каноническим уравнением гиперболы. Определение. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой, параболы. Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса
Рис. 8.4. Пусть расстояние между фокусом
Уравнение (8.4) называется каноническим уравнением параболы.
Линейная функция. Функция График линейной функции является прямой. Свойства линейной функции: 1). Область определения функции: 2). Область значений: 3). Линейная функция не является ни четной, ни нечетной.
Квадратичная функция Квадратичной называется функция вида График функции Свойства квадратичной функции: 1). Область определения функции: 2). Область значений: 3). Координаты вершины параболы 4). Если 5). Прямая Пример квадратичной функции
Гипербола Функция вида График функции Свойства функции обратной пропорциональности: 1). Область определения функции: 2). Область значений: 3). Функция нечетна. 4). Функция не пересекает координатные оси. 5). При 6). Функция убывает на промежутках 7). Прямые
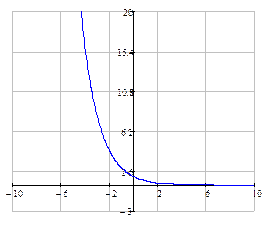
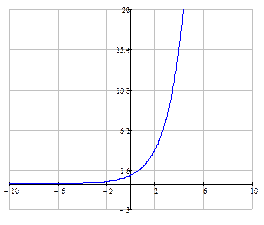
Показательная функция Функция вида Свойства показательной функции: 1). Область определения функции: 2). Область значений: 3). Если 4). При При Примеры показательных функций
Логарифмическая функция Логарифмической функцией называется функция вида Логарифмическая функция является функцией, обратной показательной. Свойства логарифмической функции: 1). Область определения функции: 2). Область значений: 3). Функция не является ни четной, ни нечетной. 4). Функция непрерывна и не имеет ни наибольшего, ни наименьшего значений. 5). При 6). При
Предел функции. Пусть функция Обозначение: Запишем это определение коротко:
Геометрический смысл предела функции поможет понять рис. 13.1. Для любой Пусть функция Обозначение: Запишем определение предела функции коротко:
что для всех точек этой окрестности соответствующие значения функции Если рассматривается поведение функции при Пусть Запишем определение коротко:
Если функция Пусть функция Обозначение: Коротко определение:
Геометрический смысл определения: для любой окрестности На экзамене достаточно привести классическое определение (1 случай). Но как выглядит определение для других случаев знать надо (это всегдашний дополнительный вопрос!)
Рекуррентные уравнения. Определение. Если каждый последующий член числовой последовательности Простейшими примерами таких последовательностей являются хорошо знакомые со школы арифметическая и геометрическая прогрессии. Если задано рекуррентное соотношение k -го порядка, то ему удовлетворяет бесконечно много последовательностей. Дело в том, что первые k элементов последовательности можно задать совершенно произвольно - между ними нет никаких соотношений. Но если первые k элементов заданы, то все остальные элементы определяются совершенно однозначно - элемент Пользуясь рекуррентным соотношением и начальными членами, можно один за другим выписывать члены последовательности, причем рано или поздно получим любой ее член. Однако при этом придется выписать и все предыдущие члены - ведь не узнав их, мы не узнаем и последующих членов. Но во многих случаях нужно узнать только один определенный член последовательности, а остальные не нужны. В этих случаях удобнее иметь явную формулу для Для решения рекуррентных уравнений общих правил, вообще говоря, нет. Однако существует весьма часто встречающийся класс уравнений, решаемый единообразным методом. Это - рекуррентные уравнения вида
где Ограничимся подробным изучением линейных рекуррентных уравнений второго порядка, так как все существенные черты данной теории могут быть показаны для этого случая. Определение. Рекуррентные уравнения вида
где Пправило решения линейных рекуррентных соотношений второго порядка с постоянными коэффициентами. Пусть дано рекуррентное соотношение (23.2):
Составим квадратное уравнение
которое называется характеристическим для данного уравнения.
При решении квадратного уравнения могут получиться:
1. Два различных корня
Задача 23.1. Найдите решение рекуррентного уравнения
Решение. Для него характеристическое уравнение имеет вид
Корнями этого квадратного уравнения являются числа
Поэтому общее решение нашего рекуррентного уравнения имеет вид Подставим Следовательно, 2. Два корня совпадают
Задача 23.2. Найдите решение рекуррентного уравнения
Решение. Для него характеристическое уравнение имеет вид
Корнем этого квадратного уравнения является число 2. Итак, общее решение нашего рекуррентного соотношения имеет вид Подставим Следовательно, 3. Оба корня характеристического уравнения комплексные числа:
где Задача 23.3. Найдите решение рекуррентного уравнения
Решение. Для него характеристическое уравнение имеет вид
Корни этого квадратного уравнения: Таким образом. Наконец, Итак, общее решение нашего рекуррентного соотношения имеет вид Подставим Следовательно, Примеры разобраны для вас, их рассказывать на надо. Производящие функции. Пусть Определение. Обозначение: Любой многочлен можно считать записью формального степенного ряда, в котором все коэффициенты, начиная с какого-то номера, равны нулю. Определение. Формальный степенной ряд
Название формальный ряд для данной последовательности означает, что (24.1) мы трактуем только как удобную запись нашей последовательности - в данном случае несущественно, для каких (действительных или комплексных) значений переменной
Для произвольных рядов мы определим операцию сложения:
операцию умножения на число с (действительное или комплексное):
и произведение
где
Из математического анализа известно, что если ряд (24.1) сходится в некоторой окрестности нуля, то его сумма является аналитической функцией в этой окрестности и
Более того, когда Таким образом, будем писать, например,
и т.д. Если вспомнить формулу бинома Ньютона
И положить в этом равенстве
Мы видим, что Теория графов. Основные понятия теории графов. Определение. Если на плоскости задать конечное множество V точек и конечный набор линий Х, соединяющих некоторые пары из точек V, то полученная совокупность точек и линий будет называться графом. При этом элементы множества V называются вершинами графа, а элементы множества Х – ребрами. В множестве V могут встречаться одинаковые элементы, ребра, соединяющие одинаковые элементы называются петлями. Одинаковые пары в множестве Х называются кратными (или параллельными) ребрами. Количество одинаковых пар (v, w) в Х называется кратностью ребра (v, w). Множество V и набор Х определяют граф с кратными ребрами – псевдограф. G = (V, X) Псевдограф без петель называется мультиграфом. Если в наборе Х ни одна пара не встречается более одного раза, то мультиграф называется графом. Если пары в наборе Х являются упорядочными, то граф называется ориентированным или орграфом. Графу соответствует геометрическая конфигурация. Вершины обозначаются точками (кружочками), а ребра – линиями, соединяющими соответствующие вершины. Определение. Если х = { v, w } –
|
|||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 533; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.058 с.) |

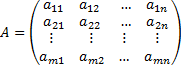 или
или  ,
,
 .
.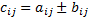 .
.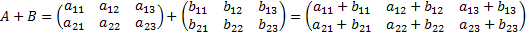
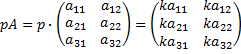 или (Cij)=(paij)
или (Cij)=(paij)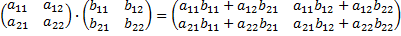
 , называется число равное
, называется число равное 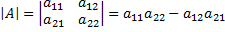 .
.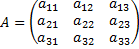 , называется число равное
, называется число равное  .
.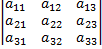

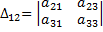
 называется его минор взятый со знаком
называется его минор взятый со знаком 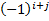 .
.
 ,
,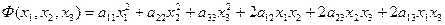
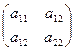 . Определитель этой матрицы называется определителем квадратичной формы.
. Определитель этой матрицы называется определителем квадратичной формы.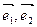 . Каждая точка плоскости имеет в этом базисе координаты х1, х2.
. Каждая точка плоскости имеет в этом базисе координаты х1, х2.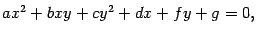
 - вещественные числа, и хотя бы одно из чисел
- вещественные числа, и хотя бы одно из чисел  отлично от нуля.
отлично от нуля.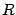 с центром в точке
с центром в точке  имеет уравнение:
имеет уравнение: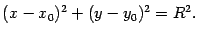 (8.1.)
(8.1.)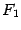 и
и 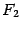 - фокусы эллипса. Начало
- фокусы эллипса. Начало 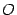 системы координат расположим на середине отрезка
системы координат расположим на середине отрезка 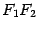 . Ось
. Ось 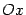 направим вдоль этого отрезка, ось
направим вдоль этого отрезка, ось 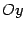 - перпендикулярно к этому отрезку (рис. 8.2).
- перпендикулярно к этому отрезку (рис. 8.2).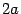 , а расстояние между фокусами -
, а расстояние между фокусами - 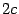 . Тогда в выбранной системе координат эллипс имеет уравнение:
. Тогда в выбранной системе координат эллипс имеет уравнение: 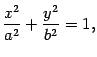 (8.2)
(8.2)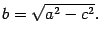
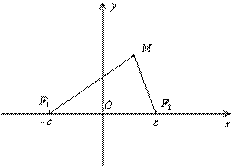
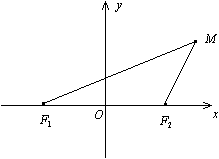
 (8.3)
(8.3)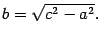
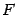 опустим перпендикуляр
опустим перпендикуляр 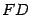 на директрису
на директрису  . Начало координат
. Начало координат  . Ось
. Ось 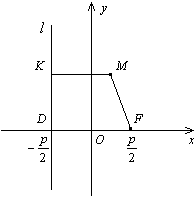
 . Тогда в выбранной системе координат парабола имеет уравнение
. Тогда в выбранной системе координат парабола имеет уравнение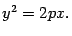 (8.4)
(8.4)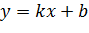 называется линейной функцией.
называется линейной функцией. .
.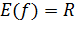 .
.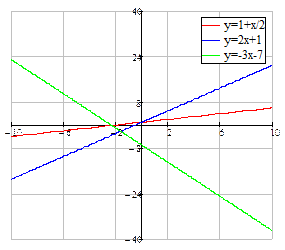 Примеры линейных функций:
Примеры линейных функций: , где
, где 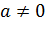 ,
, 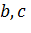 – любые действительные числа.
– любые действительные числа.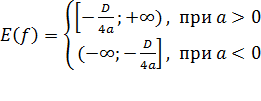 .
.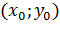 :
: 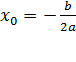 ,
, 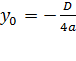 .
.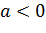 , то ветви параболы направлены вниз. Если
, то ветви параболы направлены вниз. Если 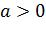 – вверх.
– вверх.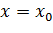 является осью симметрии графика квадратичной функции.
является осью симметрии графика квадратичной функции.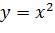 :
: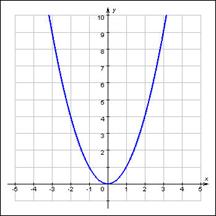
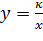 , где
, где 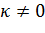 , (
, (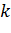 - коэффициент обратной пропорциональности) называется функцией обратной пропорциональности.
- коэффициент обратной пропорциональности) называется функцией обратной пропорциональности.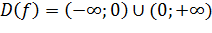 .
.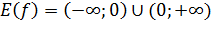 .
.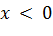
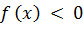 , при
, при 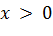
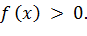
 и
и 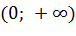 .
. и
и 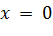 являются асимптотами (при
являются асимптотами (при  и
и 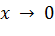 соответственно).
соответственно).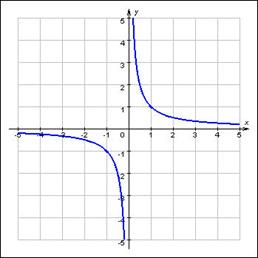
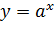 , при
, при 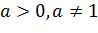 называется показательной функцией с основанием
называется показательной функцией с основанием 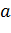 .
.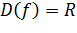
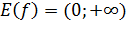 .
.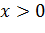 , то
, то 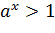 и если
и если 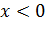 , то
, то 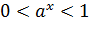 .
. функция строго монотонно возрастает на всей числовой прямой.
функция строго монотонно возрастает на всей числовой прямой.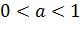 функция строго монотонно убывает на всей числовой прямой.
функция строго монотонно убывает на всей числовой прямой.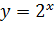 и
и 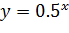 :
:
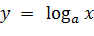 , при
, при  .
.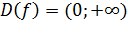
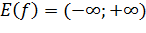 .
.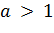 функция строго возрастает, а при
функция строго возрастает, а при 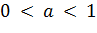 строго убывает.
строго убывает.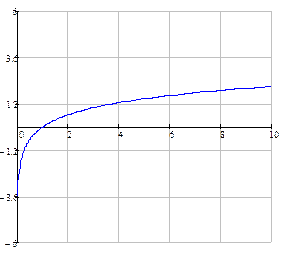
 Пример логарифмических функций
Пример логарифмических функций  и
и  :
: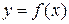 определена в некоторой окрестности точки
определена в некоторой окрестности точки  , кроме, быть может, самой точки
, кроме, быть может, самой точки  .
.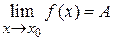 .
.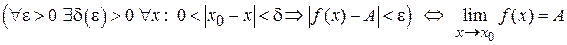 .
.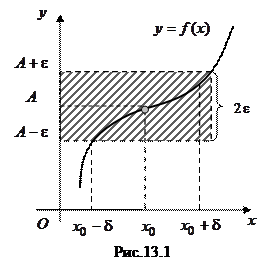 Квантор всеобщности
Квантор всеобщности 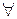 читается: «для всех». Квантор существования
читается: «для всех». Квантор существования  заменяет слово «существует». Запись
заменяет слово «существует». Запись 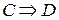 означает, что «из
означает, что «из  следует
следует  ». А
». А 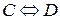 указывает на эквивалентность высказываний
указывает на эквивалентность высказываний 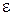 -окрестности точки
-окрестности точки  (ось
(ось  ) найдется такая
) найдется такая 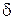 -окрестность точки
-окрестность точки 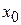 (ось
(ось  ), что для всех точек этой окрестности, кроме, быть может,
), что для всех точек этой окрестности, кроме, быть может, 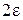 , ограниченной прямыми
, ограниченной прямыми 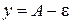 ,
, 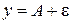 . Величина
. Величина 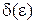 .
.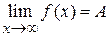 .
. .
.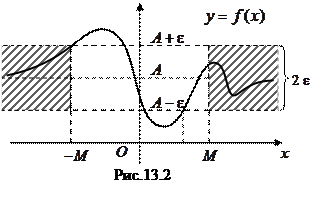 Геометрический смысл этого определения: для любой e‑окрестности точки
Геометрический смысл этого определения: для любой e‑окрестности точки 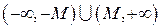 (ось
(ось 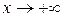 или при
или при  , то пишут
, то пишут 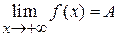 и, соответственно,
и, соответственно, 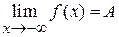 .
.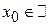 . Определение. Функция
. Определение. Функция  (включая бесконечность), если
(включая бесконечность), если  .
.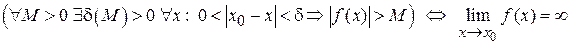 .
.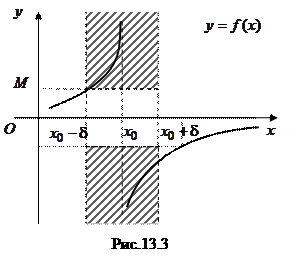 Геометрический смысл определения: для любой окрестности бесконечно удаленной точки
Геометрический смысл определения: для любой окрестности бесконечно удаленной точки 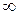 , т. е. точки графика лежат выше прямой
, т. е. точки графика лежат выше прямой  и ниже прямой
и ниже прямой 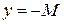 (рис. 13.3).
(рис. 13.3). , а если, принимая лишь отрицательные значения, то пишут
, а если, принимая лишь отрицательные значения, то пишут 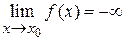 .
.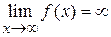 .
.
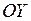 найдется такая окрестность
найдется такая окрестность 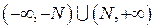 бесконечно удаленной точки оси
бесконечно удаленной точки оси 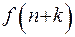 выражается через предыдущие
выражается через предыдущие  ,
, 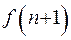 ,…,
,…, 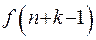 и при этом определены первые k ее членов, то говорят, что последовательность задана рекуррентно. Само число k назвается степенью, либо глубиной рекуррентности.
и при этом определены первые k ее членов, то говорят, что последовательность задана рекуррентно. Само число k назвается степенью, либо глубиной рекуррентности.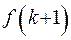 выражается в силу рекуррентного соотношения через
выражается в силу рекуррентного соотношения через  ; элемент
; элемент 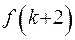 - через
- через 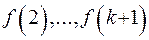 и т.д.
и т.д.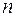 -го члена последовательности. И когда ставится задача нахождения формулы общего члена последовательности, заданной рекуррентным соотношением, употребляется термин рекуррентное уравнение. Явно заданная последовательность, удовлетворяющая рекуррентному уравнению, называется решением этого уравнения.
-го члена последовательности. И когда ставится задача нахождения формулы общего члена последовательности, заданной рекуррентным соотношением, употребляется термин рекуррентное уравнение. Явно заданная последовательность, удовлетворяющая рекуррентному уравнению, называется решением этого уравнения. , (23.1)
, (23.1) - некоторые числа. Такие уравнения называют линейными однородными рекуррентными уравнениями с постоянными коэффициентами.
- некоторые числа. Такие уравнения называют линейными однородными рекуррентными уравнениями с постоянными коэффициентами.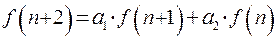 (23.2)
(23.2)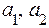 - некоторые числа, называют линейными однородными рекуррентными уравнениями второго порядка с постоянными коэффициентами.
- некоторые числа, называют линейными однородными рекуррентными уравнениями второго порядка с постоянными коэффициентами.
 , (23.3)
, (23.3)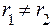 ,
,  , тогда общее решение уравнения (23.2) имеет вид
, тогда общее решение уравнения (23.2) имеет вид (23.4)
(23.4)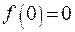 ,
, 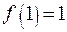
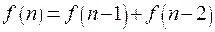 , при
, при 
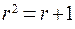
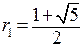 ,
, 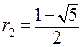 .
.
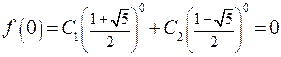 , отсюда
, отсюда 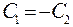 и
и 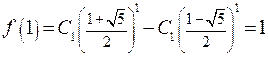 , откуда
, откуда 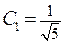 и
и 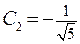 .
. .
.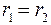 ,
, 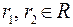 , тогда общее решение уравнения (23.2) имеет вид
, тогда общее решение уравнения (23.2) имеет вид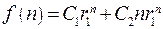 (23.5)
(23.5)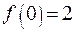 ,
, 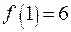 ,
,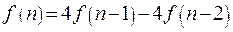 , при
, при 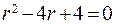
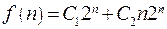 .
.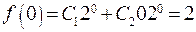 , отсюда
, отсюда  и
и  , откуда
, откуда  .
.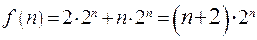 .
.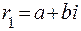 ,
, 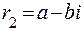 , тогда общее решение уравнения (23.2) имеет вид
, тогда общее решение уравнения (23.2) имеет вид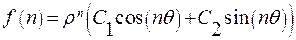 , (23.6)
, (23.6)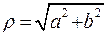 ,
,  ,
, 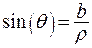 .
.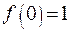 ,
, 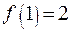 ,
,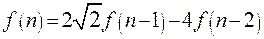 , при
, при 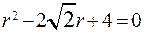
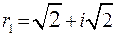 ,
,  .
. ,
,  ,
, 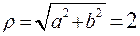 .
. и
и  , поэтому
, поэтому 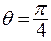
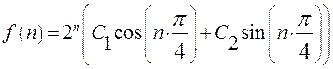 .
.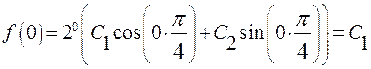 , отсюда
, отсюда 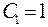 и
и  , откуда
, откуда 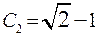 .
.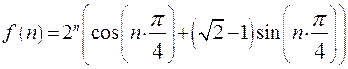 .
.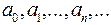 - числовая последовательность,
- числовая последовательность,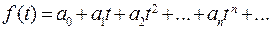 , где числа
, где числа  называется переменной,называется формальным степенным рядом.
называется переменной,называется формальным степенным рядом.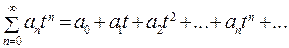 (24.1)
(24.1)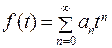 называется производящей функцией последовательности
называется производящей функцией последовательности 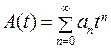 ,
, 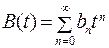
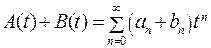 (24.2)
(24.2)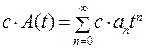 (24.3)
(24.3)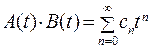 (24.4)
(24.4)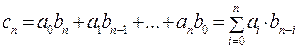 (24.5)
(24.5)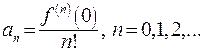 (24.6)
(24.6)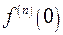 обозначает значение n -ой производной функции
обозначает значение n -ой производной функции 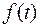 для
для  . Ряд (24.1) не что иное, как знакомый из курса математического анализа ряд Маклорена функции
. Ряд (24.1) не что иное, как знакомый из курса математического анализа ряд Маклорена функции 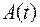 ,
, 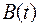 являются аналитическими функциями в окрестности нуля, то формулы (24.2)-(24.4) будут справедливы, если
являются аналитическими функциями в окрестности нуля, то формулы (24.2)-(24.4) будут справедливы, если 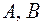 в точке
в точке 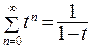 , (24.7)
, (24.7)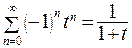 , (24.8)
, (24.8)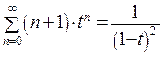 , (24.9)
, (24.9) , (24.10)
, (24.10)
 , то получим
, то получим
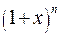 является производящей функцией для чисел
является производящей функцией для чисел 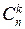 ,
,  . С помощью этой производящей функции можно сравнительно просто доказать многие свойства чисел
. С помощью этой производящей функции можно сравнительно просто доказать многие свойства чисел 


