
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы о дифференцируемых функциях и их применение.Содержание книги
Поиск на нашем сайте
Определение. Функция называется дифференцируемой, если во всех точках данного множества имеет производную. Определение. Пусть функция Теорема 17.1. (Ферма) Пусть функция Доказательство. Если производная в точке экстремума не существует, то утверждение теоремы верно. Предположим, что производная 1. Пусть функция имеет в точке 2. Пусть теперь функция Аналогично, при Замечание. Заметим, что условие
Рис.17.1. Поведение функции в окрестности точки экстремума
Геометрический смысл. Касательная, проведённая в точке экстремума, горизонтальна (если эта касательная существует). Пример 17.1. Функция
Рис. 17.2.График Пример 17.2. Функция имеет на отрезке
Рис. 17.3.График Далее мы будем предполагать, что функция Теорема 17.2. (Ролля) Пусть функция Доказательство. Так как функция 1. Если 2. Если же Замечание. Теорему можно переформулировать так: между двумя корнями Геометрический смысл. Условие
Рис.17.4. Теорема Ролля не утверждает, что корень Теорема 17.3. (Лагранжа) Пусть функция Доказательство. Сведём доказательство к применению теоремы Ролля. Для этого введём вспомогательную функцию Заметим, что Заметим теперь, что Значит, равенство
Замечание. Формулу
Если считать, что аргументу Геометрический смысл. Соединим конечные точки графика
Рис.17.5.Касательная в некоторой точке параллельна хорде Теорема утверждает, что к графику дифференцируемой функции можно провести в некоторой точке
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 629; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.26 (0.006 с.) |

 определена на некотором множестве
определена на некотором множестве  , и
, и  . Назовём точку
. Назовём точку  точкой максимума функции
точкой максимума функции 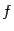 на множестве
на множестве 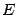 , если при всех
, если при всех  выполняется неравенство
выполняется неравенство 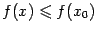 , и точкой минимума, если при всех
, и точкой минимума, если при всех  . Точка
. Точка  , являющаяся либо точкой максимума, либо точкой минимума, называется точкой экстремума.
, являющаяся либо точкой максимума, либо точкой минимума, называется точкой экстремума. -окрестность
-окрестность  точки
точки  , либо производная в точке
, либо производная в точке  существует. Рассмотрим два случая.
существует. Рассмотрим два случая. при всех
при всех  , поскольку
, поскольку  , то
, то  , и поэтому
, и поэтому 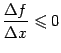 . При вычислении производной мы переходим к пределу при
. При вычислении производной мы переходим к пределу при  в этом разностном отношении. При этом знак нестрогого неравенства сохраняется, когда мы берём предел справа:
в этом разностном отношении. При этом знак нестрогого неравенства сохраняется, когда мы берём предел справа: 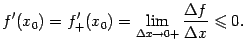 Аналогично, при
Аналогично, при  ,
,  , и поэтому
, и поэтому  . Отсюда, вычисляя предел слева, получаем:
. Отсюда, вычисляя предел слева, получаем:  Итак, выполняются два неравенства:
Итак, выполняются два неравенства:  и
и  , что возможно лишь при
, что возможно лишь при  при всех
при всех  в разностном отношении, получаем:
в разностном отношении, получаем: 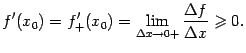
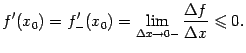 Из неравенств
Из неравенств  наклона касательной к графику
наклона касательной к графику  , проведённой при
, проведённой при  , равен 0.
, равен 0.
 имеет на отрезке
имеет на отрезке  точку минимума
точку минимума  . Производная функции существует при всех
. Производная функции существует при всех  :
:  . В точке минимума производная, действительно, оказывается равной 0:
. В точке минимума производная, действительно, оказывается равной 0:  , так что утверждение теоремы Ферма выполнено.
, так что утверждение теоремы Ферма выполнено.
 не существует. (Производная существует при всех
не существует. (Производная существует при всех  , она равна 1 при
, она равна 1 при 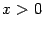 и
и 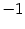 при
при  .) Итак, в точке минимума этой функции производная не существует, и утверждение теоремы Ферма снова выполнено.
.) Итак, в точке минимума этой функции производная не существует, и утверждение теоремы Ферма снова выполнено.
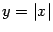
 , удовлетворяет следующим условиям: она непрерывна на отрезке
, удовлетворяет следующим условиям: она непрерывна на отрезке  ; существование односторонних производных в точках
; существование односторонних производных в точках  и
и  , вообще говоря, не предполагается. Непрерывность во всех внутренних точках отрезка, конечно, следует из предположенной дифференцируемости, а вот непрерывность в точках
, вообще говоря, не предполагается. Непрерывность во всех внутренних точках отрезка, конечно, следует из предположенной дифференцируемости, а вот непрерывность в точках  . Тогда найдётся хотя бы одна точка
. Тогда найдётся хотя бы одна точка  , в которой
, в которой  и минимальное значение
и минимальное значение  в некоторых точках
в некоторых точках  и
и  этого отрезка. Рассмотрим два случая.
этого отрезка. Рассмотрим два случая. , то наибольшее и наименьшее значения функции совпадают, и, следовательно, функция постоянна на отрезке
, то наибольшее и наименьшее значения функции совпадают, и, следовательно, функция постоянна на отрезке  . Значит,
. Значит, 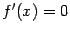 при всех
при всех  , и в качестве
, и в качестве  , то либо
, то либо  , поскольку по предположению доказываемой теоремы,
, поскольку по предположению доказываемой теоремы, 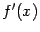 (то есть точка
(то есть точка 

 ,
,  , то есть
, то есть 
 и
и  . Так как функция
. Так как функция  дифференцируема при всех
дифференцируема при всех  , то функция
, то функция  .
.
 (17.1)
(17.1)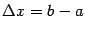 , то функция получает приращение
, то функция получает приращение  (При этом мы не считаем, что
(При этом мы не считаем, что  и
и  стремятся к 0, то есть это конечные, а не бесконечно малые, приращения). При этих обозначениях формулу (17.1) мы можем записать в виде
стремятся к 0, то есть это конечные, а не бесконечно малые, приращения). При этих обозначениях формулу (17.1) мы можем записать в виде 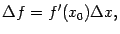 здесь участвуют конечные приращения аргумента и функции. Поэтому формулу (17.1) называют формулой конечных приращений.
здесь участвуют конечные приращения аргумента и функции. Поэтому формулу (17.1) называют формулой конечных приращений.
 ) будет равен углу наклона хорды
) будет равен углу наклона хорды  (
( ).
).


