
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрицы смежности и инцидентностиСодержание книги Поиск на нашем сайте
Пусть D =(V, X) ориентированный граф, V ={ v 1,..., v n}, X ={ x 1,..., x m}. Матрица смежности ориентированного графа D − квадратная матрица A (D)=[ aij ] порядка n, где
Матрица инцидентности − матрица B (D)=[ bij ] порядка n ´ m, где
Матрицей смежности неориентированного графа G =(V, X) называется квадратная симметричная матрица A (G)=[ aij ] порядка n, где
Для ориентированного графа
Матрицей инцидентности графа G называется матрица B (G)=[ bij ] порядка n ´ m, где
Связность. Компоненты связности Подграфом графа G (ориентированного графа D) называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G (D). Подграф называется собственным, если он отличен от самого графа. Говорят, что вершина w ориентированного графа D (графа G) достижима из вершины v, если либо w = v, либо существует путь (маршрут) из v в w. Граф (ориентированный граф) называется связным (сильно связным), если для любых двух его вершин v, w существует маршрут (путь), соединяющий v и w. Компонентой связности графа G (сильной связности ориентированного графа D) называется его связный (сильно связный) подграф, не являющийся собственным подграфом никакого другого связного (сильно связного) подграфа графа G (ориентированного графа D).
Матрицы достижимости и связности Пусть A (D) – матрица смежности ориентированного псевдографа D =(V, X) (или псевдографа G =(V, X)), где V ={ v 1,…, v n}. Обозначим через Ak =[ a ( k ) ij ] k -ю степень матрицы смежности A (D). Элемент a ( k ) ij матрицы Ak ориентированного псевдографа D =(V, X) (псевдографа G =(V, X)) равен числу всех путей (маршрутов) длины k из vi в vj. Матрица достижимости ориентированного графа D − квадратная матрица T (D)=[ tij ] порядка n, элементы которой равны
Матрица сильной связности ориентированного графа D − квадратная матрица S (D)=[ sij ] порядка n, элементы которой равны
Матрица связности графа G − квадратная матрица S (G)=[ sij ] порядка n, элементы которой равны
Утверждение 3. Пусть D =(V, X) – ориентированный граф, V ={ v 1,…, v n}, A (D) – его матрица смежности. Тогда 1) T (D)=sign[ E + A + A 2+ A 3+… A n-1], 2) S (D)= T (D)& TT (D) (TT -транспонированная матрица, &- поэлементное умножение). Пусть G =(V, X) – граф, V ={ v 1,…, v n}, A (G) – его матрица смежности. Тогда S (G)=sign[ E + A + A 2+ A 3+… A n-1] (E - единичная матрица порядка n).
Расстояния в графе Пусть Расстояние в графе удовлетворяют аксиомам метрики 1) 2) 3) 4) Пусть Диаметром графа G называется величина Пусть Максимальным удалением (эксцентриситетом) в графе G от вершины Радиусом графа G называется величина Центром графа G называется любая вершина
Образ и прообраз вершины и множества вершин Пусть
Обозначим
Нагруженные графы Нагруженный граф − ориентированный граф D =(V, X), на множестве дуг которого определена некоторая функция Цифра над дугой (см. рис. 5)− вес дуги (цена дуги).
Рис. 5. Обозначения: для любого пути П нагруженного ориентированного графа D через l (П) сумму длин дуг, входящих в путь П. (Каждая дуга считается столько раз, сколько она входит в путь П). Величина l называется длиной пути. Если выбрать веса равными 1, то придем к ненагруженному графу. Путь в нагруженном ориентированном графе из вершины v в вершину w, где v ¹ w, называется минимальным, если он имеет наименьшую длину. Аналогично определяется минимальный путь в нагруженном графе. Введем матрицу длин дуг C (D)=[ cij ] порядка n, причем
Свойства минимальных путей в нагруженном ориентированном графе 1) Если для " дуги 2) если 3) если
Деревья и циклы Граф G называется деревом если он является связным и не имеет циклов. Граф G называется лесом если все его компоненты связности - деревья. Свойства деревьев: Следующие утверждения эквивалентны: 1) Граф G есть дерево. 2) Граф G является связным и число его ребер ровно на 1 меньше числа вершин. 3) " две различные вершины графа G можно соединить единственной (и при этом простой) цепью. 4) Граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один и притом простой цикл Утверждение 4. Если у дерева G имеется, по крайней мере, 1 ребро, то у него найдется висячая вершина. Утверждение 5. Пусть G связный граф, а Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом. Пусть G – связный граф. Тогда остовное дерево графа G должно содержать n (G)-1 ребер. Значит, для получения остовного дерева из графа G нужно удалить Число Решение контрольных задач
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 627; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

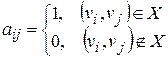

 .
.




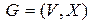 - граф (или псевдограф). Расстоянием между вершинами
- граф (или псевдограф). Расстоянием между вершинами  называется минимальная длина пути между ними, при этом
называется минимальная длина пути между ними, при этом  ,
,  , если не
, если не  пути.
пути. ,
, 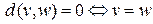
 (в неориентированном графе)
(в неориентированном графе)
 в связном неориентированном графе.
в связном неориентированном графе.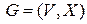 связный граф (или псевдограф).
связный граф (или псевдограф). .
. .
. называется величина
называется величина  .
.
 такая, что
такая, что  .
. ориентированный граф
ориентированный граф  - некоторая вершина
- некоторая вершина 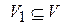 .
. - образ вершины
- образ вершины  - прообраз вершины
- прообраз вершины  - образ множества вершин V1;
- образ множества вершин V1; - прообраз множества вершин V1.
- прообраз множества вершин V1. , которую называют весовой функцией.
, которую называют весовой функцией.


 , то " минимальный путь (маршрут) является простой цепью;
, то " минимальный путь (маршрут) является простой цепью; минимальный путь (маршрут) то для " i, j:
минимальный путь (маршрут) то для " i, j: 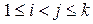 путь (маршрут)
путь (маршрут)  тоже является минимальным;
тоже является минимальным; − минимальный путь (маршрут) среди путей (маршрутов) из v в w, содержащих не более k +1 дуг (ребер), то
− минимальный путь (маршрут) среди путей (маршрутов) из v в w, содержащих не более k +1 дуг (ребер), то  − минимальный путь (маршрут) из v в u среди путей (маршрутов), содержащих не более k дуг (ребер).
− минимальный путь (маршрут) из v в u среди путей (маршрутов), содержащих не более k дуг (ребер). получается из G в результате удаления вершины
получается из G в результате удаления вершины  ребер.
ребер. называется цикломатическим числом графа G.
называется цикломатическим числом графа G.


