
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составители: Н.И. Житникова, Г.И. Федорова, А.К. ГалимовСодержание книги
Поиск на нашем сайте
Составители: Н.И. Житникова, Г.И. Федорова, А.К. Галимов УДК 519.6 (07) ББК 22.193 (я7)
Теория графов: Практикум по дисциплине «Дискретная математика». /Уфимск. гос. авиац. техн. ун-т; Сост. Н.И. Житникова, Г.И. Федорова, А.К. Галимов. - Уфа, 2005. - 39 с.
Практикум содержит основные сведения о теории графов, примеры решения контрольных задач и задания для самостоятельной работы. Предназначен для студентов факультета информатики и робототехники специальности 010503: «Математическое обеспечение и администрирование информационных систем» и направления 230100: «Информатика и вычислительная техника», изучающих дисциплину «Дискретная математика».
Ил. 15. Библиогр.: 8 назв.
Рецензенты: Бронштейн Е.М. Хабибуллин Б.Н.
© Уфимский государственный авиационный технический университет, 2005 Содержание
Введение 4 1. Краткий перечень основных понятий теории графов 5 1.1. Общие понятия 5 1.2. Понятия смежности, инцидентности, степени 7 1.3. Маршруты и пути 7 1.4. Матрицы смежности и инцидентности 8 1.5. Связность. Компоненты связности 9 1.6. Матрицы достижимости и связности 9 1.7. Расстояния в графе 10 1.8. Образ и прообраз вершины и множества вершин 10 1.9. Нагруженные графы 11 1.10. Деревья и циклы 12
2. Решение контрольных задач 13 2.1. Компоненты сильной связности ориентированного графа 13 2.2. Расстояния в ориентированном графе 16 2.3. Минимальный путь в нагруженном ориентированном графе 20 2.4. Эйлеровы циклы и цепи 23 2.5. Минимальное остовное дерево 25 2. 6. Задача о коммивояжёре 27
3. Задания для самостоятельного решения 35
Список литературы 38 ВВЕДЕНИЕ Теория графов – это математический аппарат для формализации (моделирования) реальных задач по исследованию свойств конечных множеств с заданными отношениями между их элементами. В их числе задачи из области администрирования сетей, информационных потоков, планирования, проектирования и управления различными системами. Задачи на графах удобно переводить на языки программирования, то есть решать с использованием современной вычислительной техники. Умение решать задачи на графах позволит будущему специалисту приобрести опыт разработки технологий и методов теории операций для решения задач при научных исследованиях и проектно-конструкторской деятельности В данном практикуме рассмотрены основные типы задач на графах, подходы и методы их решения, конкретные примеры. Цель раздела «Теория графов» состоит в формировании у студентов умений и навыков, необходимых при исследовании различных систем и проектировании технических объектов. Для достижения указанной цели решаются следующие задачи: - формирование знаний методов и алгоритмов эффективного решения задач дискретной оптимизации; - формирование умений и навыков использования изученных методов для решения типовых задач математического моделирования и оценки пределов применимости полученных результатов. Краткий перечень основных понятий теории графов Общие понятия Графы помогают описывать и исследовать различные системы объектов и их связи. Например, в графе, изображенном на рис. 1, точки (вершины графа) можно интерпретировать как города, а линии, соединяющие вершины (ребра), как дороги, соединяющие эти города.
Рис. 1.
Формальное определение графа таково [1-8]. Графом Г=(V, X) называется пара множеств: V – множество, элементы которого называются вершинами, X – множество неупорядоченных пар вершин, называемых ребрами. Если v, w Î V, x=(v,w)ÎX, то говорят, что ребро x соединяет вершины v и w или x инцидентно v и w. Таким образом, {v,w} – обозначение ребра. Если Х представляет собой упорядоченные пары (т. Е. X – подмножество декартова произведения V×V), то граф называется ориентированным, а пары {v,w} называют дугами. Если множеству X принадлежат пары v = w, то такие ребра (v, v) называют петлями. Существование одинаковых пар {v,w} соответствует наличию параллельных или кратных ребер (дуг), а кратностью ребер называют количество таких одинаковых пар. Например, кратность ребра { v 1,v2} в графе, изображенном на рис. 2, равна двум, кратность ребра { v 3,v4} − трем.
Рис.2.
Псевдограф − граф, в котором есть петли и/или кратные ребра. Мультиграф − псевдограф без петель.
Заметим, что графом также называют мультиграф, в котором ни одна пара не встречается более одного раза. Итак, используемые далее обозначения: V – множество вершин; X – множество ребер или дуг; v (или vi)– вершина или номер вершины; G, G 0 – неориентированный граф; D, D 0 – ориентированный; { v, w } − ребра неориентированного графа; { v, v } – обозначение петли; (v, w) − дуги в ориентированном графе; v, w – вершины, x, y, z – дуги и ребра; n (G), n (D) количество вершин графа; m (G) – количество ребер, m (D) – количество дуг. Примеры 1) Ориентированный граф D =(V, X), V ={ v 1, v 2, v 3, v 4}, X ={ x 1=(v 1, v 2), x 2=(v 1, v 2), x 3=(v 2, v 2), x 4=(v 2, v 3)}.
Рис. 3.
2) Неориентированный граф, изображенный на рис. 4: G =(V, X), V ={ v 1, v 2, v 3, v 4, v 5}, X ={ x 1={ v 1, v 2}, x 2={ v 2, v 3}, x 3={ v 2, v 4}, x 4={ v 3, v 4}}.
Рис. 4.
Маршруты и пути Последовательность v 1 x 1 v 2 x 2 v 3… x k v k+1, (где k ³1, v iÎ V, i =1,…, k +1, x iÎ X, j =1,…, k), в которой чередуются вершины и ребра (дуги) и для каждого j =1,…, k ребро (дуга) x j имеет вид { vj, vj +1} (для ориентированного графа (vj, vj +1)), называется маршрутом, соединяющим вершины v 1 и vk +1 (путем из v 1 в vk +1).
Пример В графе, изображенном на рис.4, v 1 x 1 v 2 x 2 v 3 x 4 v 4 x 3 v 2 – маршрут, v 2 x 2 v 3 x 4 v 4 – подмаршрут; маршрут можно восстановить и по такой записи x 1 x 2 x 4 x 3; если кратности ребер (дуг) равны 1, можно записать и так v 1 v 2 v 3 v 4 v 2.
Цепь − незамкнутый маршрут (путь), в котором все ребра (дуги) попарно различны. Цикл − замкнутая цепь (в неориентированном графе). Контур − замкнутый путь (в ориентированном графе). Простой путь (цепь) − путь (цепь, цикл, контур), в котором ни одна дуга/ребро не встречается дважды. Простой цикл (контур) − цикл (контур), в котором все вершины попарно различны. Гамильтонова цепь (путь, цикл, контур) − простая цепь (путь, цикл, контур), проходящая через все вершины. Эйлерова цепь (путь, цикл, контур) − цепь (путь, цикл, контур), содержащая все ребра (дуги) графа по одному разу. Длина маршрута (пути) − число ребер в маршруте (дуг в пути). Утверждение 1. Для того чтобы связный псевдограф G обладал Эйлеровым циклом, необходимо и достаточно, чтобы степени всех его вершин были четными. Утверждение 2. Для того чтобы связный псевдограф G обладал Эйлеровой цепью, необходимо и достаточно, чтобы он имел ровно 2 вершины нечетной степени.
Расстояния в графе Пусть Расстояние в графе удовлетворяют аксиомам метрики 1) 2) 3) 4) Пусть Диаметром графа G называется величина Пусть Максимальным удалением (эксцентриситетом) в графе G от вершины Радиусом графа G называется величина Центром графа G называется любая вершина
Нагруженные графы Нагруженный граф − ориентированный граф D =(V, X), на множестве дуг которого определена некоторая функция Цифра над дугой (см. рис. 5)− вес дуги (цена дуги).
Рис. 5. Обозначения: для любого пути П нагруженного ориентированного графа D через l (П) сумму длин дуг, входящих в путь П. (Каждая дуга считается столько раз, сколько она входит в путь П). Величина l называется длиной пути. Если выбрать веса равными 1, то придем к ненагруженному графу. Путь в нагруженном ориентированном графе из вершины v в вершину w, где v ¹ w, называется минимальным, если он имеет наименьшую длину. Аналогично определяется минимальный путь в нагруженном графе. Введем матрицу длин дуг C (D)=[ cij ] порядка n, причем
Свойства минимальных путей в нагруженном ориентированном графе 1) Если для " дуги 2) если 3) если
Деревья и циклы Граф G называется деревом если он является связным и не имеет циклов. Граф G называется лесом если все его компоненты связности - деревья. Свойства деревьев: Следующие утверждения эквивалентны: 1) Граф G есть дерево. 2) Граф G является связным и число его ребер ровно на 1 меньше числа вершин. 3) " две различные вершины графа G можно соединить единственной (и при этом простой) цепью. 4) Граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один и притом простой цикл Утверждение 4. Если у дерева G имеется, по крайней мере, 1 ребро, то у него найдется висячая вершина. Утверждение 5. Пусть G связный граф, а Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом. Пусть G – связный граф. Тогда остовное дерево графа G должно содержать n (G)-1 ребер. Значит, для получения остовного дерева из графа G нужно удалить Число Решение контрольных задач Пример Выделим компоненты связности ориентированного графа, изображенного на рис. 6. В данной задаче количество вершин n= 5.
Рис. 6.
Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом
Найдем матрицу достижимости для данного ориентированного графа по формуле 1) из утверждения 3:
Следовательно,
Таким образом, матрица сильной связности, полученная по формуле 2) утверждения 3, будет следующей:
Присваиваем p =1 Вычеркиваем из матрицы S 1(D) строку и столбец, соответствующие вершине v 1, чтобы получить матрицу S 2(D):
Присваиваем p =2. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы S 2(D), то есть
Вычеркиваем из матрицы S 2(D) строки и столбцы, соответствующие вершинам из V 2,чтобы получить матрицу S 3(D), которая состоит из одного элемента:
и присваиваем p =3. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:
Пример Найдем расстояния в ориентированном графе D, изображенном на рис. 7. В данной задаче количество вершин n= 7, следовательно, матрицы смежности и минимальных расстояний между вершинами ориентированного графа D будут иметь размерность 7×7.
Рис.7.
Матрица смежности:
Начинаем заполнять матрицу R (D) минимальных расстояний: сначала ставим нули по главной диагоналии rij = aij, если aij =1, (т.е. переносим единицы из матрицы смежности). Рассматриваем первую строку. Здесь есть две единицы, то есть из первой вершины за один шаг можно попасть во вторую и шестую. Из второй вершины можно попасть за один шаг в третью (путь в первую вершину нас не интересует), следовательно, можно записать
Таким образом, диаметром исследуемого ориентированного графа будет Для каждой вершины заданного ориентированного графа найдем максимальное удаление (эксцентриситет) в графе G от вершины нее по формуле, которая была приведена выше r (v 1)=3, r (v 2)=3, r (v 3)=5, r (v 4)=4, r (v 5)=2, r (v 6)=2, r (v 7)=3. Значит, радиусомграфа G будет Соответственно, центрами графа G будут вершины v 5 и v 6, так как величины их эксцентриситетов совпадают с величиной радиуса Опишем теперь нахождение минимального пути из вершины v 3 в вершину v 6 по алгоритму фронта волны. Обозначим вершину v 3 как V 0, а вершину v 6 - как W (см. рис. 8).
Рис.8.
Множество вершин, принадлежащих образу V 0, состоит из одного элемента - это вершина v 4, которую, согласно алгоритму, обозначаем как V 1: FW 1(v 3)={ v 4}. Поскольку искомая вершина не принадлежит фронту волны первого уровня
Пример Найдем минимальный путь из вершины v 2 в v 6 в ориентированном нагруженном графе D, изображенном на рис. 9. В рассматриваемом графе количество вершин n= 7, следовательно, матрица длин дуг ориентированного графа D будет иметь размерность 7×7.
Рис. 9.
Матрица длин дуг для рассматриваемого графа будет выглядеть следующим образом:
Согласно алгоритму, составляем таблицу стоимости минимальных путей из вершины v 2 в вершину vi не более, чем за k шагов, k =0,… n -1 (n =7, следовательно, k =0,…6). Как было определено выше,
В конечном итоге получаем следующую таблицу:
Теперь необходимо по построенной таблице и по матрице C (D) восстановить минимальный путь из вершины v 2 в v 6, который будет строиться с конца, то есть, начиная с вершины v 6. Для этого выбираем минимальное из чисел, стоящих в строке, соответствующей v 6 в таблице. Это число – 21 – длина минимального искомого пути. В первый раз такая длина была получена при количестве шагов, равном 4. В вершину v 6 мы можем попасть за один шаг из вершин v 1 и v 7 (длина соответствующих дуг 8 и 5 соответственно – данные из матрицы C (D)). Выбираем минимальную по длине из этих дуг. Далее, в вершину v 7 можно попасть из v 4 и v 5 (длина соответствующих дуг 7 и 3 соответственно). Продолжая аналогичным образом, найдем искомый путь за 4 шага минимальной длины из вершины v 2 в v 6: v 2 v 3 v 5 v 7 v 6.
Эйлеровы циклы и цепи Найти Эйлерову цепь в неориентированном псевдографе. Исходя из утверждений 1 и 2, чтобы найти Эйлерову цепь, нужно соединить две вершины с нечетными степенями фиктивным ребром. Тогда задача сводится к нахождению Эйлерова цикла по приведенному ниже алгоритму. Из найденного цикла удаляется фиктивное ребро, тем самым находится искомая Эйлерова цепь. Минимальное остовное дерево Найти минимальное остовное дерево в неориентированном нагруженном графе. Алгоритм выделения минимального остовного дерева в неориентированном нагруженном графе G 1) Выберем в графе G ребро минимальной длины. Вместе с инцидентными ему двумя вершинами оно образует подграф G 2 графа G. Положим 2) Если i = n (G), то задача решена и Gi – искомое минимальное остовное дерево графа G. Иначе переходим к шагу 3). 3) Строим граф Gi +1. Для этого добавим к графу Gi новое ребро минимальной длины из оставшихся, которое инцидентно какой-либо вершине графа Gi и одновременно вершине, не содержащейся в Gi. Вместе с этим ребром включаем в Gi +1 и эту инцидентную ему вершину. Присваиваем i:= i +1 и переходим к шагу 2). Пример. Найдем минимальное остовное дерево в неориентированном нагруженном графе, изображенном на рис.14.
Рис.14.
Обозначим ребро, соединяющее вершины vi и vj через xij. Для удобства использования приведенного выше алгоритма решения поставленной задачи, составим матрицу длин ребер. В рассматриваемом графе количество вершин n= 8, следовательно, матрица длин ребер графа G будет иметь размерность 8×8 и выглядеть следующим образом:
Согласно приведенному выше алгоритму, выбираем ребро минимальной длины (выбираем среди элементов матрицы C (G), минимальное − это c 47=1) и вместе с инцидентными ему двумя вершинами относим к графу G 2. Таким образом,
Поскольку i =8= n (G), работа алгоритма заканчивается. Таким образом, искомое минимальное остовное дерево графа G − граф G 8, изображенный на рис. 15, длина которого равна 22.
Рис.15.
Задача о коммивояжёре Найти в нагруженном неориентированном графе гамильтонов цикл минимального веса. Эта задача имеет практическую интерпретацию, благодаря которой и получила своё название: коммивояжёр (бродячий торговец) должен выйти из первого города, посетить по разу в неизвестном порядке города 2,3.. n и вернуться в первый город. Стоимости проезда между городами известны. В каком порядке следует объезжать города, чтобы замкнутый путь (тур) коммивояжера был наименее затратным? Сформулируем задачу в терминах теории графов, введя следующие обозначения: пусть D =[ V, X ] – полный ориентированный граф и f: X ® Следует заметить, что требование полноты ориентированного графа (наличие дороги из любого города в любой) можно опустить. Однако в этом случае гамильтонов цикл может и не существовать (по теореме, для его существования достаточна полнота орграфа). Следовательно, описываемый метод ветвей и границ приведёт к полному перебору всех вариантов незаконченных циклов прежде, чем станет очевиден факт отсутствия решения. Очевидно, cij следует трактовать как стоимость проезда из города i в город j. Допустим, что добрый мэр города j издал указ выплачивать каждому въехавшему в город коммивояжеру $5. Это означает, что любой тур подешевеет на $5, поскольку в любом туре нужно въехать в город j. Но поскольку все туры равномерно подешевели, то прежний минимальный тур будет и теперь стоить меньше всех. Добрый же поступок мэра можно представить как уменьшение всех чисел j -го столбца матрицы M на 5. Если бы мэр хотел спровадить коммивояжеров из j -го города и установил награду за выезд в размере $10, это можно было бы выразить вычитанием 10 из всех элементов j -й той строки. Это снова бы изменило стоимость каждого тура, но минимальный тур остался бы минимальным. Итак, доказана следующая лемма. Вычитая любую константу из всех элементов любой строки или столбца матрицы C, мы оставляем минимальный тур минимальным. В этой связи введем следующие термины. Пусть имеется некоторая числовая матрица. Привести строку этой матрицы означает выделить в строке минимальный элемент (его называют константой приведения) и вычесть его из всех элементов этой строки. Очевидно, в результате в этой строке на месте минимального элемента окажется нуль, а все остальные элементы будут неотрицательными. Аналогичный смысл имеют слова «привести столбец матрицы». Привести матрицу по строкам означает, что все строки приводятся. Аналогичный смысл имеют слова «привести матрицу по столбцам». Приведение матрицы означает сначала приведение этой матрицы по строкам, а затем по столбцам. Если с помощью приведённой матрицы удастся построить такую последовательность переходов по городам (по вершинам графа), которым соответствует последовательность нулевых элементов приведенной матрицы, то ясно, что для этой матрицы мы получим минимальный тур. Но он же будет минимальным и для исходной весовой матрицы С, только для того, чтобы получить правильную стоимость тура, нужно будет прибавить все константы приведения. Таким образом, сумма констант приведения играет роль оценки снизу для стоимости всех туров. Весом элемента матрицы называют сумму констант приведения матрицы, которая получается из данной матрицы заменой обсуждаемого элемента на ¥. Следовательно, слова «самый тяжёлый нуль в матрице» означают, что в матрице подсчитан вес каждого нулевого элемента, а затем фиксирован нуль с максимальным весом. Продемонстрируем теперь метод ветвей и границ для решения задачи о коммивояжёре. Пусть требуется найти легчайший простой остовной ориентированный цикл в полном взвешенном ориентированном графе на пяти вершинах, со следующей весовой матрицей C:
Верхняя строка и левый столбец, выделенные затемненным фоном, содержат номера вершин графа; символ ¥, стоящий на главной диагонали означает отсутствие дуг-петель; кроме того, символ ¥ здесь и всюду означает «компьютерную бесконечность», то есть самое большое из возможных в рассмотрении чисел; считается, что в сумме ¥ с любым числом даёт ¥. Обозначим за Г множество всех обходов коммивояжера (т. е. всех простых ориентированных остовных циклов). Поскольку граф – полный, это множество заведомо не пусто. Сопоставим ему число j(Г), которое будет играть роль значения на этом множестве оценочной функции: это число равно сумме констант приведения данной матрицы весов дуг графа и является оценкой снизу для стоимости минимального тура коммивояжёра. Приведённую матрицу весов данного графа следует запомнить, обозначим ее через С 1. Подсчитаем j(Г). Для этого выполним приведение матрицы весов. Сначала – по строкам:
Теперь − по столбцам:
Сумма констант приведения j(Г)=4+4+2+1+2+1=14. Обозначим полученную матрицу через С 1 и найдём в ней самый тяжёлый нуль. Заметим, что замена нулевого элемента на ¥ приводит к изменению лишь двух слагаемых суммы констант приведения j(Г) – по одному при приведении строк и столбцов. Поэтому вес нуля можно определить суммированием наименьших элементов его строки и столбца. Вообще нуль в клетке (i, j) приведённой матрицы означает, что цена перехода из города i в город j равна 0. А если мы не пойдём из города i в город j? Тогда все равно нужно въехать в город j за минимальную цену, указанные в j -том столбце; и все равно надо будет выехать из города i за минимальную цену, указанную в i -той строке. А это и есть оценка нуля. Например, вес нуля в первой строке и четвёртом столбце складывается из минимума по первой строке, равного 4 (c 1,2= c 1,3=4), и минимума по четвёртому столбцу, равного 0 (c 5,4=0), без учета самого c 1,4. Итак, запишем приведённую матрицу еще раз, указывая рядом с каждым нулем его вес:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 517; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.119.149 (0.017 с.) |





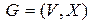 - граф (или псевдограф). Расстоянием между вершинами
- граф (или псевдограф). Расстоянием между вершинами  называется минимальная длина пути между ними, при этом
называется минимальная длина пути между ними, при этом  ,
,  , если не
, если не  пути.
пути. ,
, 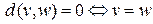
 (в неориентированном графе)
(в неориентированном графе)
 в связном неориентированном графе.
в связном неориентированном графе.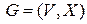 связный граф (или псевдограф).
связный граф (или псевдограф). .
. .
. называется величина
называется величина  .
.
 такая, что
такая, что  .
. , которую называют весовой функцией.
, которую называют весовой функцией.


 , то " минимальный путь (маршрут) является простой цепью;
, то " минимальный путь (маршрут) является простой цепью; минимальный путь (маршрут) то для " i, j:
минимальный путь (маршрут) то для " i, j: 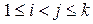 путь (маршрут)
путь (маршрут)  тоже является минимальным;
тоже является минимальным; − минимальный путь (маршрут) среди путей (маршрутов) из v в w, содержащих не более k +1 дуг (ребер), то
− минимальный путь (маршрут) среди путей (маршрутов) из v в w, содержащих не более k +1 дуг (ребер), то  − минимальный путь (маршрут) из v в u среди путей (маршрутов), содержащих не более k дуг (ребер).
− минимальный путь (маршрут) из v в u среди путей (маршрутов), содержащих не более k дуг (ребер). получается из G в результате удаления вершины
получается из G в результате удаления вершины  ребер.
ребер. называется цикломатическим числом графа G.
называется цикломатическим числом графа G.
 .
.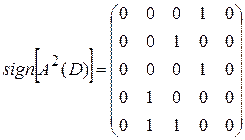 ,
, 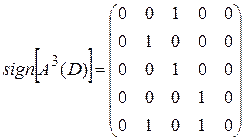 ,
, ,
,
 .
. .
. и составляем множество вершин первой компоненты сильной связности D 1: это те вершины, которым соответствуют единицы в первой строке матрицы S (D). Таким образом, первая компонента сильной связности состоит из одной вершины
и составляем множество вершин первой компоненты сильной связности D 1: это те вершины, которым соответствуют единицы в первой строке матрицы S (D). Таким образом, первая компонента сильной связности состоит из одной вершины  .
. .
. . Составляем матрицу смежности для компоненты сильной связности
. Составляем матрицу смежности для компоненты сильной связности  исходного графа D − в ее качестве возьмем подматрицу матрицы A (D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V 2:
исходного графа D − в ее качестве возьмем подматрицу матрицы A (D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V 2: .
.
 .
.



 .
. . Из шестой вершины можем добраться за один шаг в пятую и седьмую, а значит,
. Из шестой вершины можем добраться за один шаг в пятую и седьмую, а значит,  ,
,  . Теперь ищем маршруты, исходящие из первой вершины, состоящие из 3 шагов: за 2 шага идем в третью вершину, оттуда за один шаг попадаем в четвертую, поэтому
. Теперь ищем маршруты, исходящие из первой вершины, состоящие из 3 шагов: за 2 шага идем в третью вершину, оттуда за один шаг попадаем в четвертую, поэтому  . В итоге получаем следующую матрицу:
. В итоге получаем следующую матрицу: .
. .
.
 .
.
 , продолжаем работу алгоритма. Строим фронт волны второго уровня - это множество вершин, принадлежащих образу вершины V 1: FW 2(v 3)={ v 7}, обозначаем v 7≡ V 2. В образ вершины V 2 входят две вершины - v 5 и v 4, но, так как v 4 уже была помечена как V 0, то фронт волны третьего уровня состоит из одного элемента: FW 3(v 3)={ v 5}, v 5≡ V 3. Из непомеченных вершин в образ вершины V 3 входят v 1 и v 2, соответственно, FW 4(v 3)={ v 1, v 2}, v 1≡ V 4, v 2≡ V 4. Теперь помечены все вершины, кроме v 6, которая входит в образ вершины
, продолжаем работу алгоритма. Строим фронт волны второго уровня - это множество вершин, принадлежащих образу вершины V 1: FW 2(v 3)={ v 7}, обозначаем v 7≡ V 2. В образ вершины V 2 входят две вершины - v 5 и v 4, но, так как v 4 уже была помечена как V 0, то фронт волны третьего уровня состоит из одного элемента: FW 3(v 3)={ v 5}, v 5≡ V 3. Из непомеченных вершин в образ вершины V 3 входят v 1 и v 2, соответственно, FW 4(v 3)={ v 1, v 2}, v 1≡ V 4, v 2≡ V 4. Теперь помечены все вершины, кроме v 6, которая входит в образ вершины  , то есть FW 5(v 3)={ v 6≡ W }, работа алгоритма закончена. Минимальный путь (5 шагов) из вершины v 3 в вершину v 6: v 3 v 4 v 7 v 5 v 1 v 6.
, то есть FW 5(v 3)={ v 6≡ W }, работа алгоритма закончена. Минимальный путь (5 шагов) из вершины v 3 в вершину v 6: v 3 v 4 v 7 v 5 v 1 v 6.
 .
. , и
, и  для всех остальных вершин vi ≠ v 2, то есть первый столбец таблицы состоит из элементов, равных
для всех остальных вершин vi ≠ v 2, то есть первый столбец таблицы состоит из элементов, равных  , кроме элемента
, кроме элемента  , складываем элементы столбца
, складываем элементы столбца  и первого столбца матрицы стоимости и выбираем минимальное из получившихся чисел:
и первого столбца матрицы стоимости и выбираем минимальное из получившихся чисел: .
.
 i:=2.
i:=2.

 . Длина дерева G 2 будет равна l (G 2)= c 47=1. Поскольку
. Длина дерева G 2 будет равна l (G 2)= c 47=1. Поскольку  , продолжаем работу алгоритма. По четвертой и седьмой строкам ищем минимальное число (за исключением использованной единицы) − ребро минимальной длины, инцидентное либо вершине v 4, либо v 7. Выбираем ребро x 46 с длиной c 46=3 и вместе с вершиной v 6 добавляем к графу G 2, обозначая его теперь как G 3:
, продолжаем работу алгоритма. По четвертой и седьмой строкам ищем минимальное число (за исключением использованной единицы) − ребро минимальной длины, инцидентное либо вершине v 4, либо v 7. Выбираем ребро x 46 с длиной c 46=3 и вместе с вершиной v 6 добавляем к графу G 2, обозначая его теперь как G 3: 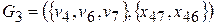 , при этом l (G 3)= c 47+ c 46=1+3=4. Аналогично находим графы:
, при этом l (G 3)= c 47+ c 46=1+3=4. Аналогично находим графы: ,
,  ;
; ,
, 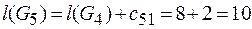 ;
; ,
, ;
; ,
, ;
;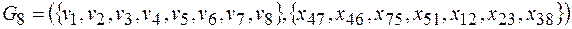 ,
, .
.
 - весовая функция, V= { v1, v2,…, vn } – множество вершин, X – множество дуг, C= { cij }, i, j =1,2… n – весовая матрица данного ориентированного графа, то есть сij = f (vi,vj), причем для любого i справедливо cii =¥. Требуется найти простой остовной ориентированный цикл (или «цикл коммивояжёра») минимального веса.
- весовая функция, V= { v1, v2,…, vn } – множество вершин, X – множество дуг, C= { cij }, i, j =1,2… n – весовая матрица данного ориентированного графа, то есть сij = f (vi,vj), причем для любого i справедливо cii =¥. Требуется найти простой остовной ориентированный цикл (или «цикл коммивояжёра») минимального веса.



