
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные числа и собственные векторы матрицы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение 9.3. Вектор х называется собственным вектором матрицы А, если найдется такое число λ, что выполняется равенство: А х = λ х, то есть результатом применения к х линейного преобразования, задаваемого матрицей А, является умножение этого вектора на число λ. Само число λ называется собственным числом матрицы А. Подставив в формулы (9.3) x`j = λxj, получим систему уравнений для определения координат собственного вектора: Отсюда Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде: получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить так: | A - λE | = 0, (9.6) поскольку в его левой части стоит определитель матрицы А-λЕ. Многочлен относительно λ | A - λE | называется характеристическим многочленом матрицы А. Свойства характеристического многочлена: 1) Характеристический многочлен линейного преобразования не зависит от выбора базиса. Доказательство. 2) Если матрица А линейного преобразования является симметрической (т.е. аij=aji), то все корни характеристического уравнения (9.6) – действительные числа. Свойства собственных чисел и собственных векторов: 1) Если выбрать базис из собственных векторов х1, х2, х3, соответствующих собственным значениям λ1, λ2, λ3 матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида: 2) Если собственные значения преобразования А различны, то соответствующие им собственные векторы линейно независимы. 3) Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.
29ВОПРОСКвадратичные формы и их матрицы. Приведение квадратичной формы к каноническому виду ортогональным преобразованием. Знакоопределённые квадратичные формы. Условия знакоопределённости квадратичных форм.
Квадратичная форма называется действительной или комплексной в зависимости от того, являются ли ее коэффициенты соответственно действительными или комплексными числами. Будем рассматривать действительные квадратичные формы. Матрицей квадратичной формы называется матрица, составленная из ее коэффициентов. Квадратичной форме (11.1) соответствует единственная симметрическая матрица
(11.3) И наоборот, всякой симметрической матрице (11.3) соответствует единственная квадратичная форма с точностью до обозначения переменных. Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма п переменных называется невырожденной, если ее матрица невырожденная, т. е. г = п, и вырожденной, если г < п.
Где А определяется формулой (11.3). Ортогональное преобразование. Для того чтобы привести квадратичную форму f(xl,x2,x3) к каноническому виду (10.4), необходимо выписать матрицу квадратичной формы
у которой A ij = Aji т. е. элементы, симметричные относительно главной диагонали, совпадают. Затем составляем и решаем характеристическое уравнение: Так как матрица симметричная, то корни λ1,λ2,λ3 характеристического уравнения являются действительные числа. Найденные собственные числа являются коэффициентами в каноническом виде квадратичной формы в базисе е'1,е'2, е'3: f(x'1,x'2, x'3)= f1x'21 + f2x'22 + f3x'23 Пусть найдены нормированные собственные векторы, соответствующие характеристическим числам γ 1 γ 2, γ3 в ортонормированном базисе е1 е2, е3: е'1 = q11 е1+ q21 е2 + q31 е3 , е'2 = q12 е1+ q22 е2 + q32 е3 , е'3 = q13 е1+ q23 е2 + q33 е3 , В свою очередь, векторы е'ь е'2, е'з образуют ортонормированный базис. Матрица является матрицей перехода от базиса e1, е2, е3 к базису е'1,е'2, е'3 Формулы преобразования координат при переходе к новому ортонор-мированному базису имеют вид: Принято говорить, что квадратичная форма f(xl,x2,x3) приведена к каноническому виду с помощью ортогонального преобразования В. Метод Лагранжа выделения полных квадратов. Пусть дана квадратичная форма (Ю.З) и пусть все коэффициенты aij (при квадратах хi2), i=1,2,3. равны нулю и в тоже время форма не равна тождественно нулю, то отлично от нуля хотя бы одно произведение, например 2al2x1x2, т. е. f(xl,x2,x3)= 2al2x1x2 Выполним преобразование базиса, при котором координаты векторов в старом и новом базисах связаны формулами: x1= x'1 - x'2 x2= x'1 + x'2 x3= x'3 Тогда f(xl,x2,x3)-2al2x1x2.= 2a12(х'12 - х'22)=2а12х'12 -2а12х'22, и так как, по предположению, а11 = а22 =0, то коэффициент при х'12 отличен от нуля. Таким образом, всегда найдется такой базис, в котором в квадратичной форме хотя бы один коэффициент при квадрате отличен от нуля.
Действительная квадратичная форма /(х,, х2, называется положитель Но-определенной, если она приводится к нормальному виду, состоящему из л положительных квадратов: /(х],х2,...,х„)~у(у1,у2,...,у„), где
Ч>(.У1,У2,-,У„) = У?+у1+-+У*, (Н.9) Т. е. если ранг и положительный индекс инерции равны числу неизвестных.
Систему значений хих2,...,хП назовем нулевой, если хх=х2=...= = х„ = О, и ненулевой, если хотя бы одно из них отлично от нуля.
Т ео рем а 11.6. Действительная квадратичная форма /(*,, *2,..., х„) является положительно-определенной тогда и только тогда, когда она принимает положительные значения при любой ненулевой системе значений переменных
*1> Х2у..., Хп.
Пусть дана квадратичная форма /(хи х2,...,хп) с матрицей А = (ац). Главными минорами квадратичной формы/называются миноры
Т. е. миноры порядка Последний из них совпадает с определителем матрицы. Теорема 11.7. Квадратичная форма Матрицей является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны. Действительная квадратичная форма называется отрицательно-определенной, если она является невырожденной и приводится к нормальному виду, содержащему только отрицательные квадраты всех переменных; эту форму можно привести к виду
Теорема 11.8. Квадратичная форма является отрицательно-определенной тогда и только тогда, когда ее главные миноры четного порядка положительны, а нечетного — отрицательны. Положительно-определенные и отрицательно-определенные квадратичные формы называются знакоопределенными квадратичными формами. Вырожденные квадратичные формы, нормальный ввд которых состоит из квадратов одного знака, называются полуопределенными. Неопределенными называются квадратичные формы, нормальный вид которых содержит как положительные, так и отрицательные квадраты переменных.
30 ВОПРОС Применение квадратичных форм к исследованию кривых и поверхностей второго порядка. Квадратичной формой
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 788; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.012 с.) |

 .
. . (9.5)
. (9.5)
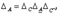 (см. (9.4)), но
(см. (9.4)), но  следовательно,
следовательно,  . Таким образом,
. Таким образом,  не зависит от выбора базиса. Значит, и | A-λE | не изменяется при переходе к новому базису.
не зависит от выбора базиса. Значит, и | A-λE | не изменяется при переходе к новому базису. (9.7) Доказательство этого свойства следует из определения собственных векторов.
(9.7) Доказательство этого свойства следует из определения собственных векторов.




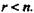





 - матрица, полученная транспонированием матрицы
- матрица, полученная транспонированием матрицы  Т. е. матрица-строка из тех же переменных, то
Т. е. матрица-строка из тех же переменных, то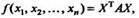 (11.4)
(11.4)








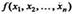


 Матрицы
Матрицы  , расположенные в левом верхнем углу;
, расположенные в левом верхнем углу;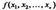 С действительной
С действительной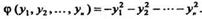 (11.10)
(11.10) от
от  неизвестных
неизвестных  называется сумма, каждое слагаемое которой является либо квадратом одного из неизвестных, либо произведением двух разных неизвестных.
называется сумма, каждое слагаемое которой является либо квадратом одного из неизвестных, либо произведением двух разных неизвестных.


