
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства бесконечно малых последовательностейСодержание книги
Поиск на нашем сайте
Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью. Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью… Сходящаяся последовательность — это последовательность элементов множества Свойства сходящихся последовательностей: Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю. Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности. Любая сходящаяся последовательность элементов хаусдорфова пространства имеет только один предел. Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится. Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом её верхний и нижний пределы совпадают. Если последовательность Сумма сходящихся последовательностей также является сходящейся последовательностью. Разность сходящихся последовательностей также является сходящейся последовательностью. Произведение сходящихся последовательностей также является сходящейся последовательностью Любую сходящуюся последовательность Всякая сходящаяся последовательность является фундаментальной. При этом фундаментальная числовая последовательность всегда сходится (как и любая фундаментальная последовательность элементов полного пространства). Монотонные поверхности. Теорема Вейерштрасса. Определение. Последовательность Определение. Последовательность Определение. Строго возрастающая или строго убывающая последовательность называется монотонной последовательностью. Теорема. Если Доказательство. При выполнении условия теоремы последовательность В силу ограниченности 1) Если последовательность не убывает, то 2) Если последовательность не возрастает, то Рассмотрим первый случай. По определению:
Т.к.
Второй случай рассматривается аналогично.
38ВОПРОСПонятие функции. Предел функции в точке и на бесконечности. Односторонние пределы. Свойства функций, имеющих предел.
Множество D называется областью определения функции и обозначается D (f (x)). Множество, состоящее из всех элементов f (x), где Число x часто называют аргументом функции или независимой переменной, а число y – зависимой переменной или, собственно, функцией переменной x. Число Преде́л фу́нкции — одно из основных понятий математического анализа. Функция Односторонние пределы Односторонние пределы § Пусть
является фильтром и обозначается § Пусть
является фильтром и обозначается Пределы на бесконечности § Пусть
§ Пусть
является фильтром и обозначается Свойства пределов функции 1) Предел постоянной величины Предел постоянной величины равен самой постоянной величине: 2) Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций. Расширенное свойство предела суммы: Предел суммы нескольких функций равен сумме пределов этих функций:
Аналогично предел разности нескольких функций равен разности пределов этих функций. 3) Предел произведения функции на постоянную величину Постоянный коэффициэнт можно выносить за знак предела:
4) Предел произведения Предел произведения двух функций равен произведению пределов этих функций:
|
|||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 255; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.174.8 (0.008 с.) |

 , имеющая предел в этом множестве.
, имеющая предел в этом множестве. сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность
сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность 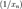 , которая является ограниченной.
, которая является ограниченной. можно представить в виде
можно представить в виде 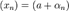 , где
, где  — предел последовательности
— предел последовательности  , а
, а  — некоторая бесконечно малая последовательность.
— некоторая бесконечно малая последовательность. не убывает (не возрастает), если
не убывает (не возрастает), если 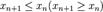 для
для  .
. возрастает (убывает), если
возрастает (убывает), если 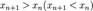 для
для  .
. - не убывает и ограничена сверху, то она сходится. Если
- не убывает и ограничена сверху, то она сходится. Если  ограниченна.
ограниченна. ,
, 


 :
: 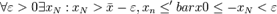
 не убывает, то при
не убывает, то при 
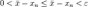 при
при 
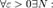 при
при  .
. Если каждому числу
Если каждому числу  поставлено в соответствие единственное число y, то говорят, что на множестве D задана числовая функция: y = f (x),
поставлено в соответствие единственное число y, то говорят, что на множестве D задана числовая функция: y = f (x), 
 называется областью значений функции и обозначается E (f (x)).
называется областью значений функции и обозначается E (f (x)). соответствующее значению
соответствующее значению  называют значением функции в точке
называют значением функции в точке  и обозначают
и обозначают  или
или 
 имеет предел
имеет предел  в точке
в точке  если для всех значений
если для всех значений  , достаточно близких к
, достаточно близких к  , значение
, значение  близко к
близко к  .
. и
и  Тогда система множеств
Тогда система множеств
 или
или  Предел
Предел  называется правосторонним пределом функции
называется правосторонним пределом функции  при
при  стремящемся к
стремящемся к 
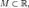 и
и  Тогда система множеств
Тогда система множеств
 или
или  Предел
Предел  называется левосторонним пределом функции
называется левосторонним пределом функции  и
и  Тогда система множеств
Тогда система множеств называется пределом функции
называется пределом функции  и
и  Тогда система множеств
Тогда система множеств
 Предел
Предел 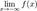 называется пределом функции
называется пределом функции  при
при 







