
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители 2 и 3-го порядков. Вычисление определителя n-го порядка. Свойства определителей 3-го порядка.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определители 2 и 3-го порядков. Вычисление определителя n-го порядка. Свойства определителей 3-го порядка. Вычисление определителей второго порядка. Определитель второго порядка (матрицы размера 2 на 2) вычисляется по правилу:
произведение элементов, стоящих на побочной. Вычисление определителей третьего порядка. Определитель третьего порядка вычисляется по правилу: Запомнить порядок сомножителей, конечно же, очень трудно, если не знать визуального представления этого правила, которое называется правило треугольников:
Здесь схематично показано, какие сомножители соседствуют в слагаемых. Определителем n-го порядка называется число, равное алгебраической сумме всевозможных произведений элементов взятых по одному и только одному из каждой строки и каждого столбца. Знак каждого слагаемого определяется числом инверсий в перестановках составленных из первых и вторых индексов сомножителей: если оно четное «+», нечетное «-». Инверсия - когда большее число стоит перед меньшим. Св-ва определителей: 1. В определителе строки и столбцы равнозначны. 2. Если все Эл-ты в строке или столбце = 0, то определитель =0.
Обратная матрица и ее построение. Теорема существования и единственности обратной матрицы. Матричный метод решения невырожденных систем линейных алгебраических уравнений. Матрица А наз. невырожденной,если ее определитель не равен 0 Матрица А-1 наз. обратной к матрице А,если АА-1= А-1А=Е, где Е-единичная матрица. Всякая невырожденная матрица имеет единствен. обратную матрицу. Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем: Пусть дана система линейных уравнений с Тогда её можно переписать в матричной форме:АХ=В, где А — основная матрица системы, В и Х — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на А-1 — матрицу, обратную к матрице А:А-1(АХ)= А-1В Так как А-1А=Е, получаемХ= А-1В. Правая часть этого уравнения даст столбец решений исходной системы
4. Ранг матрицы. Вычисление ранга матрицы методом окаймляющих миноров и с помощью элементарных преобразований. Наибольший из порядков миноров данной матрицы отличный от нуля называется рангом матрицы. rank A = rg A = r Свойства ранга: - при транспонировании матрицы ранг не меняется - если вычеркнуть из матрицы нулевую строку, то ранг не меняется - ранг матрицы не меняется при элементарных преобразованиях над строками матрицы. Максимальный порядок r отличных от нуля миноров матрицы A называется ее рангом, а любой минор порядка r, отличный от нуля - базисным минором. Основные методы вычисления ранга матрицы: Метод окаймляющих миноров. Пусть в матрице найден минор k-го порядка M, отличный от нуля. Рассмотрим лишь те миноры (k+1)− го порядка, которые содержат в себе (окаймляют) минор M: если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой минор (k+1)−го порядка, и вся процедура повторяется. Метод элементарных преобразований основан на том, что элементарные преобразования матрицы не меняют ее ранга. Используя эти преобразования матрицу можно привести к такому виду, когда все ее элементы кроме a11,a22,...,arr (r≤min(m,n)), равны нулю. Следовательно, ранг матрицы равен r.
Решение систем линейных уравнений. Теорема Кронекера-Капелли Пусть дана произвольная система n линейных уравнений с n неизвестными Исчерпывающий ответ на вопрос о совместности этой системы дает теорема Кронекера-Капелли. Теорема 4.1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы. Примем ее без доказательства. Правила практического разыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем. Теорема 4.2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Теорема 4.3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений. Формулы
Необходимость. Так как ранг не может превосходить размера матрицы, то, очевидно, r<=n. Пусть r=n. Тогда один из минеров размера nхn отличен от нуля. Поэтому соответствующаясистема линейных уравнений имеет единственное решение:
Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то r<n. Достаточность: Пусть r<n. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т. е. имеет и ненулевые решения. Пусть дана однородная система n линейных уравнений с n неизвестными
Теорема 4.5. Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определительD был равен нулю, т. е. D=0. Если система имеет ненулевые решения, то D=0. Ибо при D¹0 система имеет только единственное, нулевое решение. Если же D=0, то ранг r основной матрицы системы меньше числа неизвестных, т.е. r<n. И, значит, система имеет бесконечное множество (ненулевых) решений. Пример 4.6. Решить систему
Положив x3=0,получаем одно частное решение: x1=0, x2=0, x3=0. Положив x3=1, получаем второе частное решение: x1=2, x2=3, x3=1 и т д. Пример 4.4. Решить систему методом Гаусса:
Решение: В результате элементарных преобразований над расширенной матрицейсистемы
исходная система свелась к ступенчатой:
Поэтому общее решение системы: x2=5x4-13x3-3;x1=5x4-8x3-1 Если положить, например, x3=0,x4=0, то найдем одно из частных решений этой системы x1=-1,x2=-3,x3=0,x4=0. Поворот осей координат. Пусть даны две декартовы системы координат с одинаковым началом О и разными направлениями осей (рис. 70). Пусть α есть угол между осями Ох и ОХ. Обозначим через х, у и X, Y координаты произвольной точки М соответственно в старой и новой системах: х = | ОР |, у = | РM |, X = | ОР1 |, Y = | Р1M |. Рассмотрим ломаную линию ОР1MP и возьмем ее проекцию на ось Ох. Замечая, что проекция ломаной линии равна проекции замыкающего отрезка имеем: ОР1MP = | ОР |. (4) С другой стороны, проекция ломаной линии равна сумме проекций ее звеньев следовательно, равенство (4) запишется так: пр ОР1 + пр Р1M + пp MP =| ОР Так как проекция направленного отрезка равна его величине, умноженной на косинус угла между осью проекций и осью, на которой лежит отрезок (гл. I, § 8), то пр ОР1 = X cos α пр Р1M = Y cos (90° + α) = — Y sin α, пp MP = 0. Отсюда равенство (4') нам дает: x = X cos α — Y sin α. (5) Аналогично, проектируя ту же ломаную на ось Оу, получим выражение для у. В самом деле, имеем: пр ОР1 + пр Р1M + пp MP = пp ОР = 0. y = X sin α + Y cos α. (6) Из формул (5) и (6) мы получим новые координаты X и Y выраженными через старые х и у, если разрешим уравнения (5) и (6) относительно X и Y.
17ВопросУравнение кривых второго порядка в полярной системе координат. Общее уравнение второго порядка
1 Уравнение окружности в центре ( (х - 2 Эллипс – геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. 3 Гипербола – кривая второго порядка, которая в некоторой системе координат описывается уравнением где а > 0, b > 0 – параметры гиперболы. Точка пересечения гиперболы с осью ОХ (± а, 0) называется вершинами гиперболы. С осью ОY гипербола не пересекается. Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b)
4Парабола – кривая второго порядка, которая в некоторой системе координат описывается уравнением
18 вопрос Общее уравнение плоскости Ах + Ву + Сz + D = 0,где А, B и C не равны нулю одновременно.Коэффициенты А, B и C являются координатами нормального вектора плоскости (т.е. вектора, перпендикулярного плоскости). При А где a = – D / A, b = – D / B, c = – D / C. Эта плоскость проходит через точки (a, 0, 0), (0, b, 0) и (0, 0, с), т.е. отсекает на осях координат отрезки длиной a, b и c. Уравнение плоскости, проходящей через точку (х 0 , у 0, z 0 ) и перпендикулярной вектору (А, В, C): А (х – х 0) + В (у – у 0) + С (z – z 0) = 0. Условие параллельности плоскостей Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0: AF – BE = BG – CF = AG – CE = 0. Условие перпендикулярности плоскостей Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0: АE+ ВF+ СG = 0. Расстояние между двумя точками (х 1 , у 1, z 1 ) и(x 2, y 2, z 2):
Расстояние от точки (х 0 , у 0, z 0 ) до плоскости Ах + Ву + Сz + D = 0:
Угол
19 ВОПРОС Прямая в пространстве. Способы ее задания. Взаимное расположение двух прямых в пространстве. Угол между двумя прямыми. Уравнение прямой, проходящей через две различные точки (х 1, у 1, z 1) и (х 2, у 2 , z 2):
Параметрическое уравнение прямой, проходящей через точку (х 0 , у 0, z 0) и параллельной направляющему вектору прямой (a, b, с):
Пусть заданы две плоскости Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0, причём их нормальные векторы неколлинеарны, тогда система уравнений
описывает прямую – линию пересечения этих плоскостей. Пусть (a, b, с) и (p, q, r) – направляющие векторы двух прямых, тогда имеем условие параллельности прямых: aq – bp = br – cq = ar – cp = 0, условие перпендикулярности прямых: ap + bq + cr = 0, угол угол
Эллипсоид Каноническое уравнение эллипсоида имеет вид Из этого уравнения следует | x | < a, | у | < b, | z | < c, то есть эллипсоид заключён в прямоугольный параллелепипед со сторонами 2· а, 2· b, 2· c. Координатные плоскости являются плоскостями симметрии. Однополостный гиперболоид Каноническое уравнение однополостного гиперболоида имеет вид Координатные плоскости являются плоскостями симметрии, так как при замене х на − х, у на − у, z на − z уравнение не меняется. Двуполостный гиперболоид Каноническое уравнение двуполостного гиперболоида имеет вид
Эллиптический параболоид Каноническое уравнение эллиптического параболоида имеет вид
Гиперболический параболоид Каноническое уравнение гиперболического параболоида имеет вид
Эллиптический конус Каноническое уравнение эллиптического конуса имеет вид
Координатные плоскости являются плоскостями симметрии: при замене х на - х, у на - у, z на - z уравнение не меняется. Цилиндрической поверхностью называется поверхность, полученная движением прямой (образующей), перемещающейся параллельно некоторому вектору и пересекающей во время движения фиксированную линию (направляющую). В результате получим уравнение искомой цилиндрической поверхности F(x, y, z) = 0. Здесь уравнение направляющей определяется системой уравнений
Уравнение Эллиптический цилиндр Уравнение эллиптического цилиндра имеет вид
Гиперболический цилиндр Уравнение гиперболического цилиндра имеет вид
Параболический цилиндр Уравнение гиперболического цилиндра имеет вид y 2 = 2 p x.
ВОПРОС Эллипсоид.
При Величины Если в уравнении (7) заменить (одновременно или порознь)
Для определенности будем считать, что
Чтобы составить более точное представление об эллипсоиде, произведем сечения плоскостями, параллельными координатным плоскостям. Например, пересекая эллипсоид плоскостями
с полуосями Отсюда видно, что самый большой эллипс получается в сечении эллипсоида плоскостью Точки Если какие-либо две полуоси равны между собой, то эллипсоид (7) будет эллипсоидом вращения, т. е. получается от вращения эллипса относительно соответствующей оси координат.
23ВОПРОС Гиперболоиды. Однополостной гиперболоид – поверхность, определяемая в некоторой прямоугольной системе координат уравнением Двуполостной гиперболоид – поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением Начало координат называют центром гиперболоида. Вершина – точка пересечения гиперболоида с координатными осям. Это четыре точки однополостного гиперболоида (4.48) и две точки двуполостного гиперболоида (4.49). Три отрезка координатных осей, соединяющих вершины гиперболоидов, называются осями гиперболоидов. Оси гиперболоидов, принадлежащие координатным осям, называются поперечными осями гиперболоидов, а ось, принадлежащая оси аппликат, — продольной осью гиперболоидов. Числа, равные половинам длин осей, называются полуосями гиперболоидов. Из уравнения (1) вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат — центром симметрии однополостного гиперболоида. Уравнение (1) наз-ся каноническим уравнением однополосного гиперболоида. Если однополостный гиперболоид задан своим каноническим уравнением (1) то оси Ох, Оу и Oz наз-ся его главными осями. Установим вид поверхности (1). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения
из которых следует, что в сечениях получаются гиперболы. Теперь рассм-м сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy. Величины a, b, c называются полуосями однополосного гиперболоида. Если a=b,то гиперболоид может быть получен вращением гиперболы с полуосями а и с вокруг мнимой оси 2с.
Параболоиды. Параболо́ид ― тип поверхности второго порядка. Параболоид может быть охарактеризован как незамкнутая нецентральная (то есть не имеющая центра симметрии) поверхность второго порядка. Канонические уравнения параболоида в декартовых координатах: Z=ax2 +by2 если a и b одного знака, то параболоид называется эллиптическим. если a и b разного знака, то параболоид называется гиперболическим. если один из коэффициентов равен нулю, то параболоид называется параболическим цилиндром. Эллиптический параболоид Эллиптический параболоид при a=b=1 Эллипти́ческий параболо́ид — поверхность, описываемая функцией вида Z= Если a=b то эллиптический параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг вертикальной оси, проходящей через вершину данной параболы. Гиперболический параболоид Гиперболический параболоид при a=−b=1 Гиперболи́ческий параболо́ид (называемый в строительстве «гипар») — седлообразная поверхность, описываемая в прямоугольной системе координат уравнением вида Z= Из второго представления видно, что гиперболический параболоид является линейчатой поверхностью. Поверхность может быть образована движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх, при условии, что первая парабола соприкасается со второй своей вершиной.
25.Линейное векторное пространство. Подпространство. Линейная зависимость и независимость векторов линейного пространства. Базис и размерность линейного пространства. Координаты векторов. Преобразование координат вектора при замене базиса. Линейным действительным пространством или векторным действительным пространством наз. множество V элементов x,y,z…, для которых определены операции сложения элементов и умножения элемента на действительное число,удовлетворяющее след. аксиомам: 1. х+у=х+у, 2.(х+у)+z=x+(y+z), 3. существует элемент 0 такой, что x+0=x 4. для каждого x существует элемент -x, такой что x+(-x)=0 5. 1*x=x 6. a*(b*x)=(a*b)*x 7. (a+b)x=ax+bx 8. a(x+y)=ax+ay Множество W Ì V наз.подпространством линейного пространства V,если выполняются след. условия: 1.в множестве W определены те же операции,что и в множестве V 2.если х,у ∈ W, то х+у ∈ W 3.если х ∈ W, то αх ∈ W. Система векторов наз. линейно независимой,если линейная комбинация этих векторов λ1а1 + λ Система векторов наз. линейно зависимой,если существует такая линейная комбинация этих векторов =0,где не все λ =0 Базисом системы векторов наз. такая подсистема в которой все вектора линейно независимы и любой др. вектор явл. линейной комбинацией векторов этой подсистемы. Число n наз. размерностью линейного пространства V, если выполняются следующие условия:1. в V существует n линейно независимых векторов.2. любая система n+1 векторов из V линейно зависима. Координатами вектора х в базисе е1,е2,…,еn наз. коэффициенты α1, α2,… αn в разложении этого вектора по данному базису,т.е. в формуле х=α1е1 + α2е2+…+ αnen Если система векторов e 1,..., e n n -мерного линейного пространства Ln образует базис в L n, то любой вектор x из Ln может быть представлен в виде x = С 1· e 1+ С 2 ·e 2+...+ Сn · e n. Выражение x = С 1· e 1+ С 2 ·e 2+...+ Сn · e n называется разложением вектора по базису e 1,..., e n, а числа С 1, С 2,..., С n называются координатами вектора x в базисе e 1,..., e n. Координаты вектора принято обозначать тем же символом, что и сам вектор: x = x 1· e 1+ x 2 ·e 2+...+ xn · e n. Взаимно однозначное соответствие x = x 1· e 1+ x 2 ·e 2+...+ xn · e n ⇐⇒ x = (x 1, x 2,..., xn)— изоморфизм Ln и Rn. Преобразование координат вектора при замене базиса. Пусть системы векторов e = {e 1,..., e n } и f = {f 1,..., f n } — два базиса n -мерного линейного пространства Ln. Обозначим xe = (x 1, x 2,..., x n) и xf = (x' 1, x' 2,..., x' n) — координаты вектора x ∈ Ln соответственно в базисах e и f. Справедливо следующее xe = C e→f ·x f:
Здесь C e→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f1,..., f n в базисе e 1,..., e n: f1 = с 11· e2 + с 21 ·e1 +... + с n 1 ·e n, f2 = с 12· e1 + с 22 ·e2 +... + с n 2 ·e n, ..., f n = с 1 n · e2 +... + с nn ·e n. Формулу преобразования координат вектора при изменении базиса принято записывать в виде xf = (C e→f)− 1 ·x e
Деление многочленов Что значит разделить один многочлен P на другой Q? Это значит найти многочлены М (частное) и N (остаток), удовлетворяющие двум требованиям: 1) имеет место равенство: MQ + N = P; 2) степень многочлена N меньше степени многочлена Q.
33ВОПРОСМножества и действия над ними. Элементы математической логики. Логические символы. Множеством именуется некоторая совокупность элементов, объединенных по какому-либо признаку. Если есть такая совокупность, разумеется, как единое целое, говорят, что имеют дело с множеством. Приведенное определение не может рассматриваться как математически строгое, поскольку понятие множества является исходным, на основе него строятся остальные понятия математики. Тем не менее, из при веденного определения ясно, как можно говорить с множестве, например, действительных чисел или множестве плоских фигур. Если множество состоит из конечного числа элементов, оно называется конечным. Остальные множества называются бесконечными. Для множества используются следующие обозначения: А = {а,b,с,d} Множество, в котором не содержится ни одного элемента, называется пустым. Обозначается оно знаком Ø. Множества, состоящие из одних и тех же элементов, называют совпадающими. Например, совпадают два конечных множества, которые отличаются друг от друга порядком их элементов. Определение 1. Пересечением множеств А и В называют их общую часть С. Другими словами, пересечение множеств А и В образуют элементы, принадлежащие равно как А, так и В (обозначается пересечение - n) Определение 2. Объединением множеств А и В, называют множество С, составленное из элементов, принадлежащих хотя бы одному из этих множеств Определение 3. Разностью множеств А и В называют множество С = В / А, Многие математические понятия удобно записывать в виде выражений, содержащих некоторые логические символы. Так, символ Основной объект математической логики - высказывание. Высказыванием называется повествовательное предложение, которое может быть классифицировано либо как истинное, либо как ложное, но не как и то, и другое вместе. Если высказывание истинно, будем говорить, что его значение истинности - истина (или Высказывания в математической логике обычно обозначаются прописными латинскими буквами: Отрицание — это высказывание, которое получается из данного высказывания Простое добавление слова «не» к высказыванию чаще всего будет противоречить языковым нормам. Поэтому в конкретных случаях требуется «перевод» полученного высказывания на русский язык. Пусть, например, Отрицанием Дизъюнкция - это высказывание, которое получается из двухданных высказываний Дизъюнкция строится с помощью неисключающего «или». Таким образом, дизъюнкция Конъюнкция - это высказывание, которое получается из двух данных высказываний Импликация образуется из высказываний На примере импликации хорошо видна разница между обычным языком и языком логики. В обычном языке сложное предложение «если Импликация обозначается
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 556; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.011 с.) |

 Запомнить просто: произведение элементов, стоящих на главной диагонали, минус
Запомнить просто: произведение элементов, стоящих на главной диагонали, минус

 неизвестными (над произвольным полем):
неизвестными (над произвольным полем): 




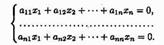



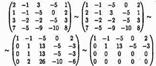


 + 2
+ 2  ху +
ху +  +
+  х +
х +  у +
у +  = 0
= 0 ;
;  ) R
) R +
+  = 1
= 1 = 2 рх где р > 0 – параметры параболы.
= 2 рх где р > 0 – параметры параболы. 0, В
0, В 


 между плоскостями Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:
между плоскостями Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:


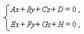


 .
. .
.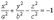 .
.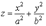 .
. .
. .
.
 определяет уравнение образующей.
определяет уравнение образующей. .
. .
.
 (7)
(7) эллипсоид (7) обращается в сферу радиуса
эллипсоид (7) обращается в сферу радиуса  с центром в начале координат, т. е. геометрическое место точек, отстоящих от начала на расстоянии
с центром в начале координат, т. е. геометрическое место точек, отстоящих от начала на расстоянии  .
. называются полуосями эллипсоида.
называются полуосями эллипсоида. на
на  ,
,  на
на  ,
,  на
на 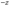 , то оно не изменится, — это показывает, что эллипсоид (7) есть поверхность, симметричная относительно координатных плоскостей
, то оно не изменится, — это показывает, что эллипсоид (7) есть поверхность, симметричная относительно координатных плоскостей  ,
,  ,
,  и начала координат. Поэтому достаточно изучить уравнение (7) в первом октанте (системы координат), т. е. для
и начала координат. Поэтому достаточно изучить уравнение (7) в первом октанте (системы координат), т. е. для  ,
,  ,
,  . Часть эллипсоида, находящаяся в первом октанте, определяется явным уравнением, например
. Часть эллипсоида, находящаяся в первом октанте, определяется явным уравнением, например ,
,  ,
,  ,
,  .
. . Эллипсоид есть ограниченная поверхность. Он находится внутри шара радиуса
. Эллипсоид есть ограниченная поверхность. Он находится внутри шара радиуса  с центром в начале координат: для координат любой точки эллипсоида
с центром в начале координат: для координат любой точки эллипсоида  имеет место неравенство
имеет место неравенство .
. , получим в сечении эллипсы
, получим в сечении эллипсы
 ,
,  .
. . Аналогичная картина будет при сечении плоскостями
. Аналогичная картина будет при сечении плоскостями  ,
,  .
. ,
,  ,
,  лежат на эллипсоиде (7) и называются его вершинами.
лежат на эллипсоиде (7) и называются его вершинами. (1)
(1) (2) В уравнениях a, b, с — положительные параметры, характеризующие гиперболоиды, причем a ≥ b.
(2) В уравнениях a, b, с — положительные параметры, характеризующие гиперболоиды, причем a ≥ b. и
и 
 или
или  из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями
из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями  и
и  ,
, величины a* и b* возрастают бесконечно.
величины a* и b* возрастают бесконечно. +
+  Где a и b одного знака. Поверхность описывается семейством параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх.
Где a и b одного знака. Поверхность описывается семейством параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх. +
+  ) (
) (
 , называемый квантором общности, используется вместо слов: «для любого», «для всех», «каково бы ни было …» и т.д., а символ
, называемый квантором общности, используется вместо слов: «для любого», «для всех», «каково бы ни было …» и т.д., а символ  – квантор существования – вместо слов «существует», «найдется хотя бы один …», «имеется» и т.д.
– квантор существования – вместо слов «существует», «найдется хотя бы один …», «имеется» и т.д. (от английского true); если - ложно, то значение истинности – ложь (
(от английского true); если - ложно, то значение истинности – ложь ( от false).
от false). ,
,  ,
,  и т.д. Для того чтобы из высказываний получать новые высказывания, применяются специальные операции - логические связки. Рассмотрим пять основных логических связок. Сначала дадим неформальное объяснение. Однако оно чревато неточностями, поэтому дадим логическим операциям также строгое определение. Определить высказывание — значит, указать, в каких случаях оно истинно, а в каких ложно.
и т.д. Для того чтобы из высказываний получать новые высказывания, применяются специальные операции - логические связки. Рассмотрим пять основных логических связок. Сначала дадим неформальное объяснение. Однако оно чревато неточностями, поэтому дадим логическим операциям также строгое определение. Определить высказывание — значит, указать, в каких случаях оно истинно, а в каких ложно. с помощью слова «не». Отрицание можно обозначать по-разному:
с помощью слова «не». Отрицание можно обозначать по-разному:  ,
,  ,
,  .
. = «Завтра пойдет дождь». Что значит «Не (Завтра пойдет дождь)»: «Дождь пойдет не завтра», «Завтра пойдет не дождь» или «Завтра не пойдет дождь»? Здравый смысл подсказывает, что отрицанием высказывания
= «Завтра пойдет дождь». Что значит «Не (Завтра пойдет дождь)»: «Дождь пойдет не завтра», «Завтра пойдет не дождь» или «Завтра не пойдет дождь»? Здравый смысл подсказывает, что отрицанием высказывания 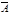 высказывания
высказывания  называется такое высказывание, которое принимает значение
называется такое высказывание, которое принимает значение  (ложно), если высказывание
(ложно), если высказывание  (истинно), если высказывание
(истинно), если высказывание  = «Завтра не пойдет дождь».
= «Завтра не пойдет дождь». с помощью союза «или». Дизъюнкция обозначается
с помощью союза «или». Дизъюнкция обозначается  .
. истинна, когда истинно, по крайней мере, одно из высказываний
истинна, когда истинно, по крайней мере, одно из высказываний  и
и  или оба вместе. Другими словами,дизъюнкция ложна в том и только в том случае, когда оба высказывания ложны.
или оба вместе. Другими словами,дизъюнкция ложна в том и только в том случае, когда оба высказывания ложны. . Конъюнкция
. Конъюнкция  справедлива в том и только в том случае, когда оба высказывания истинны.
справедлива в том и только в том случае, когда оба высказывания истинны. , при этом говорят: «
, при этом говорят: « 


