
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление определителей 2-го и 3-го порядков. Миноры, алгебраические дополнения.Содержание книги
Поиск на нашем сайте
Вычисление определителей второго порядка. Вычисление определителей третьего порядка. Определитель третьего порядка вычисляется по правилу: 40) Перемножение матриц. Нахождение обратной матрицы. Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.
Элемент
Нахождение обратной матрицы:
1)Пусть А – квадратная невырожденная матрица (определитель не равен нулю).
1)Сначала вычисляем определитель. 2)
3)Транспонируем полученную матрицу 4)Вычисляем обратную матрицу по формуле
5)Делаем проверку: A*A^-1 = E
41) Решение систем линейных уравнений матричным методом и методом Крамера:
Метод Крамера:
Система линейных уравнений:
Определители:
Решение:
Матричный метод (обратная матрица):
1)Сначала вычисляем определитель. 2)
3)Транспонируем полученную матрицу 4)Вычисляем обратную матрицу по формуле
5)Делаем проверку: X=A^-1*B
42) Геометрическим вектором называется направленный отрезок, который можно перемещать параллельно ему самому. Направленный отрезок с началом в точке A и концом в точке B обозначается AB. Когда заданы направление и длина, но не фиксируется точка приложения, говорят, что задан свободный вектор. Термин подчеркивает, что точка приложения геометрического вектора может меняться произвольно Геометрические векторы, точка приложения которых не может изменяться, называют еще связанными векторами. Линейные операции над геометрическими векторами Сложение векторов: Пусть даны два вектора
Сумму двух неколлинеарных векторов
Умножение вектора на число:
Произведением вектора
Компланарность векторов: Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. Условия компланарности векторов
Коллинеарность векторов: Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными. Условия коллинеарности векторов
Орт вектора Ортом вектора
Модуль вектора (длина вектора) |a| в прямоугольных декартовых координатах равен квадратному корню из суммы квадратов его координат. Так в случае плоской задачи модуль вектора
Свойства линейных операций над векторами
Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Для любых векторов
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 538; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.008 с.) |




 произведения матриц приведённых выше вычисляется следующим образом
произведения матриц приведённых выше вычисляется следующим образом
 , где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j Например,
, где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j Например, 
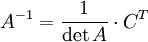 ,Ст – транспонента.
,Ст – транспонента.




 , где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j Например,
, где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j Например,  и
и  . Приложим вектор
. Приложим вектор  (концу вектора
(концу вектора  / Вектор
/ Вектор  называется суммой векторов
называется суммой векторов  . Это нахождение суммы называется правилом треугольника.
. Это нахождение суммы называется правилом треугольника. и
и  можно найти по правилу параллелограмма. Для этого откладываем от любой точки
можно найти по правилу параллелограмма. Для этого откладываем от любой точки  векторы
векторы  и
и  , а затем строим параллелограмм
, а затем строим параллелограмм  (рис. 1.7,6). Диагональ
(рис. 1.7,6). Диагональ  параллелограмма определяет сумму:
параллелограмма определяет сумму:
 на число
на число 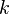 называется вектор, который:
называется вектор, который: , или противоположнонаправлен, если
, или противоположнонаправлен, если  ;
; .
. называется вектор единичной длины, имеющий то же направление, что и вектор
называется вектор единичной длины, имеющий то же направление, что и вектор  .
.







 можно найти по следующей формуле
можно найти по следующей формуле
 .
. и любых действительных чисел
и любых действительных чисел  справедливы равенства:
справедливы равенства:



