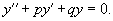Метод неопределенных коэффициентов

Правая часть f (x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов.

Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как

1. 
2. 
   где P_n (x) и Q_m (x) − многочлены степени n и m, соответственно.

В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель x^s, где s − кратность корня α в характеристическом уравнении.

В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x.

 

32) Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами(положительный дискриминант):

Рассмотрим линейное дифференциальное уравнение вида

где p, q − постоянные коэффициенты.

Для каждого такого дифференциального уравнения можно записать так называемое характерное уравнение, есть сделать замену y=k с соответствующими степенями,

:

 

Обшее решение ОДУ зависит от дискриминанта.

Возможны следующие случаи:

 

Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k ₁ и k ₂ действительны и различны. В этом случае общее решение описывается функцией

где C ₁ и C ₂ − произвольные действительные числа.

 

33) Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами(дискриминант равен нулю)

Рассмотрим линейное дифференциальное уравнение вида

где p, q − постоянные коэффициенты.

Для каждого такого дифференциального уравнения можно записать так называемое характерное уравнение, есть сделать замену y=k с соответствующими степенями,

:

 

Обшее решение ОДУ зависит от дискриминанта.

 

Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k ₁ второго порядка. Общее решение однородного дифференциального уравнения имеет вид:

 

34) Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами(отрицательный дискриминант)

 

Рассмотрим линейное дифференциальное уравнение вида

где p, q − постоянные коэффициенты.

Для каждого такого дифференциального уравнения можно записать так называемое характерное уравнение, есть сделать замену y=k с соответствующими степенями,

:

Обшее решение ОДУ зависит от дискриминанта.

Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k ₁ = α + βi, k ₁ = α − βi. Общее решение записывается в виде

 

35) Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами(метод вариаций постоянных)

Линейное неоднородное уравнение данного типа имеет вид:

где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:

Теорема: Общее решение неоднородного уравнения является суммой общего решения y ₀(x) соответствуюшего однородного уравнения и частного решения y ₁(x) неоднородного уравнения:

 

Метод вариации постоянных

Если общее решение y ₀ однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных.

Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:

Вместо постоянных C ₁ и C ₂ будем рассматривать вспомогательные функции C ₁(x) и C ₂(x). Будем искать эти функции такими, чтобы решение

удовлетворяло неоднородному уравнению с правой частью f (x).

 

36). Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и правой частью вида f(x)= P(x)e^ax, где P(x)- многочлен:

 

Линейное неоднородное уравнение данного типа имеет вид:

где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:

Теорема: Общее решение неоднородного уравнения является суммой общего решения y ₀(x) соответствуюшего однородного уравнения и частного решения y ₁(x) неоднородного уравнения: