
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исторический обзор обоснований геометрии. «Начала» Евклида.Содержание книги
Поиск на нашем сайте
 ) Аксиомы Евклида 1. Равные одному и тому же равны между собой. 2. Если к равным прибавить равные, то получим равные. 3. Если от равных отнимем равные, то получим равные. ……………………………………………………………………… 7.Совмещающиеся друг с другом равны между собой. Затем Евклид начинает развивать свою логическую дедуктивную (от общего к частному) систему. Свою геометрию Евклид подразделил на две части:1 часть – без использования 5 постулата.Определение: Геометрия, построенная на аксиомах Евклида без 5 постулата, называется абсолютной.В этой геометрической системе содержится конечное число теорем (логических следствий из аксиом и постулатов). В трактовке Евклида их 29.Евклид добавляет пятый постулат. В этой системе (в евклидовой геометрии) количество логических следствий бесконечно.Основные недостатки «Начал» Евклида.Наиболее слабое место – это определения: 1. Евклид пытается определить исключительно все понятия. 2. Определения, которые даёт Евклид, нечётки, логически неоправданны. 3. Система аксиом неполная. У него нет аксиомы непрерывности (немецкий математик Дедекинд). Отсутствуют аксиомы движения 4. Система аксиом и постулатов зависима: 4-ый постулат лишний – равенство углов можно доказать из остальных постулатов. 5. Убедительность логики Евклида во многих случаях подкрепляется привычками наших пространственных представлений. А это значит, что «Начала» логически безукоризненного обоснования геометрии не содержат.На недостатки Евклида указывал уже Архимед (жил на 100 – 150 лет позднее Евклида). Для того, чтобы сравнивать отрезки, он ввёл свою аксиому Архимеда:Для любых двух отрезков а и в(в<а) существует nє N, такое что nв >а. 16. Элементы теории Лобачевского. ) Аксиомы Евклида 1. Равные одному и тому же равны между собой. 2. Если к равным прибавить равные, то получим равные. 3. Если от равных отнимем равные, то получим равные. ……………………………………………………………………… 7.Совмещающиеся друг с другом равны между собой. Затем Евклид начинает развивать свою логическую дедуктивную (от общего к частному) систему. Свою геометрию Евклид подразделил на две части:1 часть – без использования 5 постулата.Определение: Геометрия, построенная на аксиомах Евклида без 5 постулата, называется абсолютной.В этой геометрической системе содержится конечное число теорем (логических следствий из аксиом и постулатов). В трактовке Евклида их 29.Евклид добавляет пятый постулат. В этой системе (в евклидовой геометрии) количество логических следствий бесконечно.Основные недостатки «Начал» Евклида.Наиболее слабое место – это определения: 1. Евклид пытается определить исключительно все понятия. 2. Определения, которые даёт Евклид, нечётки, логически неоправданны. 3. Система аксиом неполная. У него нет аксиомы непрерывности (немецкий математик Дедекинд). Отсутствуют аксиомы движения 4. Система аксиом и постулатов зависима: 4-ый постулат лишний – равенство углов можно доказать из остальных постулатов. 5. Убедительность логики Евклида во многих случаях подкрепляется привычками наших пространственных представлений. А это значит, что «Начала» логически безукоризненного обоснования геометрии не содержат.На недостатки Евклида указывал уже Архимед (жил на 100 – 150 лет позднее Евклида). Для того, чтобы сравнивать отрезки, он ввёл свою аксиому Архимеда:Для любых двух отрезков а и в(в<а) существует nє N, такое что nв >а. 16. Элементы теории Лобачевского. Исходным пунктом геометрии Лобачевского является принятие всех предложений геометрии Евклида, не зависящих от 5-го постулата (то есть абсолютной геометрии, включая аксиомы Паша, Архимеда, Дедекинда), и присоединение к ним взамен отброшенного 5-го постулата следующей аксиомы, противоположной аксиоме Плейфера, а значит, и 5-му постулату. Через точку, лежащую вне прямой в плоскости, определяемой ими, можно провести не менее двух прямых, не пересекающих данной прямой. Заметим, что существование хотя бы одной прямой, проходящей через данную точку и не пересекающей данной прямой, есть факт абсолютной геометрии. Аксиома Лобачевского утверждает существование по крайней мере двух таких прямых. Отсюда немедленно следует, что таких прямых существует бесконечное множество. Плоскость, в которой предполагается выполнение аксиомы Лобачевского, называется плоскостью Лобачевского. Заметим также, что геометрию Лобачевского называют гиперболической геометрией, в соответствии с чем плоскость и пространство Лобачевского называются гиперболическими. Основная теорема. Пусть в плоскости даны прямая a и не лежащая на ней точка A. Тогда в пучке прямых с центром в точке A существуют две пограничные прямые, разделяющие все прямые пучка на два класса: на класс прямых, пересекающих a, и класс прямых, не пересекающих a. Эти граничные прямые сами не пересекают a.
Рис.7 Всё сказанное приводит нас к следующей картине расположения прямых пучка с центром в точке A, взятой вне данной прямой BB'. В этом пучке существуют две граничные прямые CC' и DD' (рис.7), симметрично расположенные относительно перпендикуляра AP, опущенного из точки A на BB', и образующие с ним ےCAP=ےD'AP=α< Эти прямые, а также все прямые пучка, проходящие внутри заштрихованных вертикальных углов CAD и C'AD', не пересекают прямой BB', а все прямые пучка, проходящие внутри вертикальных углов CAD' и C'AD, пересекают BB'. Две граничные прямые CC' и DD' называются параллельными прямой BB' в точке A, причём прямая C'C называется параллельной B'B в направлении B'B, а прямая DD' называется параллельной прямой BB' в направлении BB'. Острый угол α, образуемый параллельными с перпендикуляром AP, называется углом параллельности в точке A относительно прямой BB'. Этот угол есть функция длины p перпендикуляра AP и обозначается так: α=П(p). AP называется отрезком параллельности в точке A относительно прямой BB'. Основная формула геометрии Лобачевского, устанавливающая зависимость между длиной отрезка и отвечающим ему углом параллельности, имеет вид:
Все прямые пучка, не пересекающие BB' и лежащие внутри заштрихованных вертикальных углов, называются расходящимися с BB' или сверхпараллельными к BB'; угол, образуемый такой прямой с перпендикуляром AP с обеих от него сторон, больше угла параллельности α. Наконец, все остальные прямые пучка, образующие с AP с какой-либо стороны острый угол, меньший угла параллельности α, называются пересекающими прямую BB' или сходящимися с BB'. Определение. Прямая C'C называется параллельной прямой B'B в направлении B'B (рис.8) в точке A, если, во-первых, прямая C'C не пересекает прямой BB', во-вторых, C'C является граничной в пучке прямых с центром в точке A, то есть всякий луч AE, проходящий внутри угла CAD, где D – любая точка прямой BB', пересекающей луч DB.
Рис.8 Пространство, в которой предполагается выполнение аксиомы Лобачевского, называется пространством Лобачевского. В пространстве Лобачевского параллельность и расходимость прямых, а также прямой и плоскости, определяется следующим образом: Определение. Две прямые в пространстве называются параллельными (расходящимися), если они лежат в одной плоскости и в этой плоскости они параллельны (расходятся). Определение. Прямая a называется параллельной плоскости α, если она параллельна своей проекции на эту плоскость. Определение. Прямая a называется расходящейся с плоскостью α, если она расходится со своей проекцией на эту плоскость. Из последних определений немедленно следует, что прямая, параллельная плоскости, неограниченно сближается с последней в сторону параллельности, а прямая, расходящаяся с плоскостью, имеет с этой плоскостью единственный общий перпендикуляр, в обе стороны от которого в проектирующей плоскости прямая неограниченно удаляется от плоскости. Взаимное расположение прямых и плоскостей в пространстве Лобачевского вполне характеризуется при помощи так называемого конуса параллельности, являющегося аналогом понятия угла параллельности.
Рис.9 Пусть дана плоскость α и не лежащая на ней точка A (рис. 9). Пусть AA' – перпендикуляр к α, проектирующий точку A в точку A' на плоскости α. Пусть далее AB – прямая, параллельная плоскости α, и A'B' – её проекция на α. Тогда угол BAA' есть угол параллельности в точке A прямой AB относительно прямой A'B'. Будем вращать прямую AB около перпендикуляра AA', тогда AB опишет круглую коническую поверхность с вершиной в точке A, все образующие которой параллельны плоскости α. Эта поверхность называется конусом параллельности в точке A относительно плоскости α. Таким образом, конусом параллельности в точке A относительно плоскости α называется геометрическое место всевозможных прямых, параллельных плоскости α в точке A. Из этого определения ясно, что всякая прямая, проходящая через точку A и лежащая внутри конуса параллельности, пересекает плоскость α, а всякая прямая, проходящая через точку A и лежащая вне конуса параллельности, расходится с плоскостью α. Конус параллельности в точке A позволяет все плоскости, проходящие через точку A, разбить на три категории: 1) плоскости, пересекающие конус по двум образующим, 2) плоскости, касающиеся конуса по образующей, 3) плоскости, имеющие с конусом лишь одну общую точку A. Плоскости 1-й категории содержат прямые, проходящие через A и лежащие внутри конуса параллельности, а потому эти плоскости пересекают плоскость α. При этом прямая пересечения с плоскостью α параллельна в противоположных направлениях проекциям образующих, по которым плоскость 1-й категории пересекает конус параллельности. Плоскости 2-й и 3-й категории не содержат прямых, проходящих внутри конуса параллельности, а потому не могут пересекаться с плоскостью α. Определение. Плоскость, проходящая через точку A, называется сходящейся с плоскостью α, параллельной плоскости α, или расходящейся с плоскостью α, смотря по тому, будет ли эта плоскость пересекать конус параллельности в точке A по паре образующих, или будет касаться конуса по образующей, или не будет иметь с конусом общих прямых. В плоскости Лобачевского через точку, лежащую вне прямой, проходят две прямые, параллельные данной. В пространстве Лобачевского через точку, лежащую вне плоскости, можно провести бесконечное множество прямых, параллельных данной плоскости, это и будут образующие конуса параллельности. Аксиоматический метод. Аксиоматический метод появился в Древней Греции, а сейчас применяется во всех теоретических науках, прежде всего в математике. Аксиоматический метод построения научной теории заключается в следующем: выделяются основные понятия, формулируются аксиомы теории, а все остальные утверждения выводятся логическим путём, опираясь на них. Основные понятия выделяются следующим образом. Известно, что одно понятие должно разъясняться с помощью других, которые, в свою очередь, тоже определяются с помощью каких-то известных понятий. Таким образом, мы приходим к элементарным понятиям, которые нельзя определить через другие. Эти понятия и называются основными. Когда мы доказываем утверждение, теорему, то опираемся на предпосылки, которые считаются уже доказанными. Но эти предпосылки тоже доказывались, их нужно было обосновать. В конце концов, мы приходим к недоказываемым утверждениям и принимаем их без доказательства. Эти утверждения называются аксиомами. Набор аксиом должен быть таким, чтобы, опираясь на него, можно было доказать дальнейшие утверждения. Выделив основные понятия и сформулировав аксиомы, далее мы выводим теоремы и другие понятия логическим путём. В этом и заключается логическое строение геометрии. Аксиомы и основные понятия составляют основания планиметрии. Так как нельзя дать единое определение основных понятий для всех геометрий, то основные понятия геометрии следует определить как объекты любой природы, удовлетворяющие аксиомам этой геометрии. Таким образом, при аксиоматическом построении геометрической системы мы исходим из некоторой системы аксиом, или аксиоматики. В этих аксиомах описываются свойства основных понятий геометрической системы, и мы можем представить основные понятия в виде объектов любой природы, которые обладают свойствами, указанными в аксиомах. После формулировки и доказательства первых геометрических утверждений становится возможным доказывать одни утверждения (теоремы) с помощью других. Доказательства многих теорем приписываются Пифагору и Демокриту. Гиппократу Хиосскому приписывается составление первого систематического курса геометрии, основанного на определениях и аксиомах. Этот курс и его последующие обработки назывались "Элементы".
18-19. Скалярные величины (длина отрезка, площадь многоугольника). Теорема о существования и единственности. Длиной отрезка называется положительная величина, определённая для каждого отрезка так что:1) равные отрезки имеют разные длины;2) если отрезок состоит из конечного числа отрезков, то его длина равна сумме длин этих отрезков.Рассмотрим процесс измерения длин отрезков. Из множества отрезков выбирают какой-нибудь отрезок e и принимают его за единицу длины. На отрезке а от одного из его концов откладывают последовательно отрезки равные e, до тех пор, пока это возможно. Если отрезки, равные e отложились n раз и конец последнего совпал с концом отрезка e, то говорят, что значение длины отрезка а есть натуральное число n, и пишут: а = ne. Если же отрезки, равные e, отложились n раз и остался ещё остаток, меньший e, то на нём откладывают отрезки равные e =1/10 e. Если они отложились точно n раз, то тогда а =n, n e и значение длины отрезка а есть конечная десятичная дробь. Если же отрезок e отложился n раз и остался ещё остаток, меньший e, то на нём откладывают отрезки, равные e =1/100e. Если представить этот процесс бесконечно продолженным, то получим, что значение длины отрезка, а есть бесконечная десятичная дробь. Итак, при выбранной единице, длина любого отрезка выражается действительным числом. Верно и обратное; если дано положительное действительное число n, n, n,... то взяв его приближение с определённой точностью и проведя построения, отражённые в записи этого числа, получим отрезок, численное значение длины которого, есть дробь: n,n,n …Понятие о площади фигуры имеет любой человек: мы говорим о площади комнаты, площади земельного участка, о площади поверхности, которую надо покрасить, и так далее. При этом мы понимаем, что если земельные участки одинаковы, то площади их равны; что у большего участка площадь больше; что площадь квартиры слагается из площади комнат и площади других её помещений. Это обыденное представление о площади используется при её определении в геометрии, где говорят о площади фигуры. Но геометрические фигуры устроены по-разному, и поэтому когда говорят о площади, выделяют особый класс фигур. Например, рассматривают площади многоугольников и других ограниченных выпуклых фигур, или площадь круга, или площадь поверхности тел вращения и так далее. В начальном курсе математики рассматриваются только площади многоугольников и ограниченных выпуклых плоских фигур. Такая фигура может быть составлена из других. Например, фигура F составлена из фигур F1, F2, F3. Говоря, что фигура составлена (состоит) из фигур F1, F2,…,Fn, имеют в виду, что она является их объединением и любые две данные фигуры не имеют общих внутренних точек. Площадью фигуры называется неотрицательная величина, определённая для каждой фигуры так, что: I/ равные фигуры имеют равные площади; 2/ если фигура составлена из конечного числа фигур, тоеёплощадь равна сумме их площадей. Если сравнить данное определение с определением длины отрезка, то увидим, что площадь характеризуется теми же свойствами, что и длина, но заданы они на разных множествах: длина - на множестве отрезков, а площадь - на множестве плоских фигур. Площадь фигуры F обозначать S(F). Чтобы измерить площадь фигуры, нужно иметь единицу площади. Как правило, за единицу площади принимают площадь квадрата со стороной, равной единичному отрезку e, то есть отрезку, выбранному в качестве единицы длины. Площадь квадрата со стороной e обозначают e. Например, если длина стороны единичного квадрата m, то его площадь m. Измерение площади состоит в сравнении площади данной фигуры с площадью единичного квадрата e. Результатом этого сравнения является такое число x, что S(F)=x e.Число x называют численным значением площади при выбранной единице площади. Существование и единственность перпендикуляра к прямой
Значит отрезок AB
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.232.108 (0.009 с.) |


 .
.


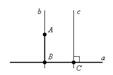 Теорема.
Теорема.  a, так как b||с и с
a, так как b||с и с 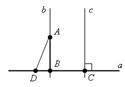 Теперь докажем единственность перпендикуляра AB.
Теперь докажем единственность перпендикуляра AB. 


