
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Согласно (22), для выполнения последнего равенства необходимо, чтобыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Условие (23) выполняется либо при d=d1 (это частный случай, см. сноску на стр.69), либо при
Период колебаний (22) оборотного маятника с учетом (24) принимает вид:
Ускорение свободного падения может быть найдено из предыдущего выражения
где (d1+d2) = Lпр - приведенная длина оборотного маятника.
Если маятник совершает N колебаний за время t, то период колебаний определяется как:
Итак, расчетная формула ускорения свободного падения с учетом (27) принимает вид:
При выполнении данной лабораторной работы на точность окончательного результата оказывают влияние ряд факторов, которые не учитываются в расчетной формуле (28).Прежде всего следует указать, что формула (28) является приближенной, так как она была получена в результате замены sinj на j (естественно, при увеличении угла отклонения маятника на углы, большие, чем 4¸50, погрешность данного эксперимента возрастает). Кроме того, для более точного расчета необходимо вводить (учитывать) поправки на температуру, т.к. изменение температуры влияет на размеры маятника из-за теплового расширения. Погрешности вносят также силы трения, действующие на маятник со стороны подвеса (опоры) и окружающего воздуха - эти причины приводят к некоторому увеличению периода колебаний физического маятника. Для устранения последних ошибок следует уменьшить трение в подвесе (используют агатовую призму) и вводить поправку на давление, учитывающую изменение влияния воздуха. Естественно, с учетом вышеуказанных поправок можно достичь весьма большой точности в определении ускорения свободного падения.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
В основании 1 установки (рис.25), которое расположено на регулируемых ножках, укреплены стойка 2 и миллисекундомер 3. На стойке, имеющей миллиметровую шкалу, установлены два кронштейна. Верхний кронштейн 4 имеет возможность поворота вокруг оси стойки 2 и быть зафиксированным с помощью винта 5. На верхнем кронштейне укреплен математический маятник, состоящий из нити 6 и шарика 7. Для изменения длины математического маятника конец нити намотан на катушку с ручкой 8. На кронштейне 4 имеется также возможность устанавливать физический маятник, который представляет собой стержень 9 с насечками 10 и наконечниками 11. На стержне 9 укреплены подвижные грузы 12 и призмы 13. Нижний кронштейн 14, несущий фотоэлектрический датчик 15, имеет возможность перемещения вдоль стойки 2 и фиксации положения на ней с помощью винта 16. На лицевой панели миллисекундомера 3 размещены табло “ПЕРИОДЫ” и “ВРЕМЯ,С”, а также кнопка “СЕТЬ” (включение сети), “СБРОС” (установка нуля измерителя) и “СТОП” (остановка счета измерителя).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Как видно из (28), для нахождения ускорения силы тяжести достаточно измерить величины: расстояние (d + d1) между опорными ребрами призм и период колебаний маятника в положении d и в “перевернутом” положении d1 T(d) = T(d1) = T. Но добиться совпадения указанных периодов практически очень сложно. Следовательно, необходимо выяснить, при каких расхождениях периодов На рис.26 представлен качественный вид зависимости периода колебаний от расстояний d и d1 опорных призм до центра масс. Из графика видно, что по каждую сторону от центра масс маятника имеется по два положения опорных призм, при которых периоды оборотного маятника совпадают (d и d1; d/ и d1/ ). Поэтому целесообразно подготовить оборотный маятник к измерениям следующим образом.
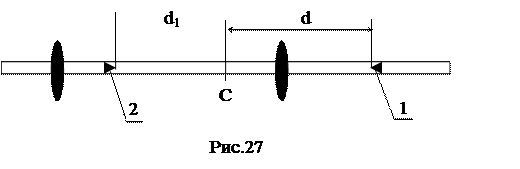
 1. Подвижные грузы (чечевицы 12, рис.25) закрепляют на стержне в несимметричных положениях (рис.27): один груз у конца стержня, а второй- вблизи его центра, т.е. центр масс системы будет находиться между грузами и, главное, смещен относительно середины стержня. 1. Подвижные грузы (чечевицы 12, рис.25) закрепляют на стержне в несимметричных положениях (рис.27): один груз у конца стержня, а второй- вблизи его центра, т.е. центр масс системы будет находиться между грузами и, главное, смещен относительно середины стержня.
2. Опорные призмы (1,2 рис.27) устанавливают так, чтобы они лезвиями были обращены друг к другу, но одна призма (2) должна находиться между подвижными грузами (приблизительно посередине), а другая (1) - вблизи другого конца стержня. 3. Грани лезвий призм должны находиться на одной линии с насечками на стержне. 4. Закрепите маятник на вкладыше верхнего кронштейна (рис.25) на призме (1, рис.27), находящейся вблизи конца стержня. 5. Опустите нижний кронштейн (14, рис.25) и поверните верхний кронштейн 4 на 180°, чтобы оборотный маятник находился над фотоэлектрическим датчиком. Переместите нижний кронштейн таким образом, чтобы наконечник стержня маятника пересекал оптическую ось: источник света - фотоэлектрический датчик. 6. Подключите миллисекундомер к сети и нажмите кнопку “СЕТЬ”. 7. Отклоните маятник на угол не более 4¸5° от положения равновесия и отпустите. 8. Нажмите кнопку “СБРОС” и после совершения оборотным маятником не менее 10 колебаний (путь N = 10) нажмите кнопку “СТОП”. 9. Запишите время t, за которое было совершено N колебаний в табл.1 измерений. 10. Повторите измерения времени t (при расстоянии d, рис.27) n = 5 раз и вычислите среднее значение <t>; результаты всех измерений и вычислений внесите в табл.1. 11. Затем, не меняя положения грузов (чечевиц) и первой призмы, устанавливают оборотный маятник на призме 2 (рис.27). Если маятник опрокидывается (это означает, что центр масс (т.С) находится выше точки вращения), то призму 2 следует сдвинуть к концу стержня. 12. Повторите пункты (5,7,8,9) данного упражнения, причем число колебаний N1 должно быть равно числу колебаний N, т.е. N1 = N = 10.
Таблица 1
13. Если оказалось, что время t1> <t>, то вторую призму следует несколько переместить к концу стержня; если t1 < <t>, то призму сдвигают чуть ближе к центру масс и снова измеряют время t1. 14. Добиваются такого положения второй призмы, при котором выполнялось бы условие:
15. Повторите измерение времени t1 (при расстоянии d1, рис.27) n = 5 раз и вычислите среднее значение <t1>; результаты измерений и вычислений внесите в табл. 1. 16. Снимите оборотный маятник с установки и измерьте приведенную длину физического маятника (Lпр = d + d1), подсчитав количество насечек на стержне между лезвиями призм (расстояние между соседними насечками 10,00 мм). Запишите значение Lпр в табл. 1. 17. Определите для расстояний d и d1 абсолютные (Dt) и относительные (Еt) в табл.1 погрешности измерений времени колебаний физического маятника, используя методику расчета погрешностей прямых измерений, которая представлена в начале данного пособия. При расчете принять коэффициент надежности a = 0,9, тогда при значении параметра n = n - 1 = 4 коэффициент Стьюдента равен ta,n-1 = t0,9;4 = 2,1. 18. Рассчитайте по формуле (28) среднее значение ускорения <g> силы тяжести по среднему значению времени <t> или <t1>, считая их очень близкими. 19. Произведите расчет относительной (Еg) и абсолютной (Dg) погрешностей по формулам:
20. Оцените расхождение полученного экспериментального результата и действительного значения ускорения силы тяжести, соответствующего широте г. Москвы gм = 9,8156 м/с2, пользуясь формулой:
20. Результат эксперимента следует записать в стандартном виде
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ СРАВНЕНИЕ ПЕРИОДОВ КОЛЕБАНИЙ ФИЗИЧЕСКОГО И
1. Нижний кронштейн 14 (рис.25) с фотоэлектрическим датчиком установите в нижней части стойки 2, чтобы указатель положения кронштейна фиксировал длину, равную приведенной длине физического маятника, указанной в табл.1. 2. Поверните верхний кронштейн 4 так, чтобы над нижним кронштейном 14 располагался математический маятник. 3. Вращая ручку 8 катушки, установите высоту шарика таким образом, чтобы черта на шарике была продолжением черты на корпусе нижнего кронштейна. Итак, длина математического маятника равна приведенной длине физического маятника. 4. Подключите миллисекундомер к сети и нажмите кнопку “СЕТЬ”. 5. Отклоните шарик на угол не более 4 ¸ 5° от положения равновесия перпендикулярно световому лучу фотоэлектрического датчика и отпустите (без толчка). 6. Нажмите кнопку "СБРОС" и после совершения не менее 10 колебаний (пусть N = 10 колебаний) нажать кнопку "СТОП". 7. Результат полученного времени запишите в табл. 2. 8. Повторите данный эксперимент 5 раз и по найденному среднему значению времени <t>, за которое совершается N = 10 полных колебаний, определите среднее значение периода <T> математического маятника:
9. По формуле (19) рассчитайте период (Tр) колебаний математического маятника с длиной L = Lпр и величину Tp внесите в табл.2. 10. Сравните результат экспериментальных и расчетных величин периодов физического и математического маятников и объясните причины расхождения их значений. Таблица 2
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Выведите формулу ускорения свободного падения на поверхности Земли, зная массу Земли, ее радиус и гравитационную постоянную. 2. Как изменится ускорение свободного падения на высоте h = R3 над поверхностью Земли? 3. По какой формуле можно оценить ускорение свободного падения в шахте глубиной 200 м? 4. Что такое математический маятник? 5. Дайте определение физического маятника. 6. Что такое период колебаний, и какова его единица измерения? 7. Что характеризует момент инерции твердого тела (относительно оси)? 8. Какова формула момента инерции твердого тела (относительно оси)? 9.Дайте определение теоремы Штейнера. 10. Определите величину и направление момента силы F относительно неподвижного центра (точки О).
12. Выведите формулу периода колебаний физического маятника. 13. Что такое приведенная длина физического маятника? 14. Что такое центр масс системы материальных точек или твердого тела?
16. Кратко сформулируйте порядок выполнения лабораторной работы с оборотным физическим маятником. 17. Как влияет на точность эксперимента увеличение угла отклонения маятника от положения равновесия? 18. Почему необходимо производить измерения на двух призмах? 19. Какие Вы знаете виды измерений? 20. Назовите типы погрешностей измерений. 21. Как вычисляется абсолютная погрешность прямых измерений? 22. По какой методике оценивается погрешность косвенных измерений? 23. Объясните, что такое доверительный интервал? 24. Что такое коэффициент надежности? 25. Каковы виды систематических ошибок? 26. Как суммируются случайные и систематические ошибки? 27. Зачем вычисляется относительная ошибка? 28. Какова окончательная запись результата измерений? 29. Каковы правила округления? 30.Какова точность значений постоянных?
Лабораторная работа № 9 ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ ЦЕЛЬ РАБОТЫ
Экспериментальная проверка основного закона динамики вращательного движения. Определение момента инерции тела относительно оси, проходящей через центр масс тела.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Маятник Максвелла представляет собой (рис.29) диск 6, закрепленный на оси 7, подвешенный на бифилярном подвесе. Движение маятника (диска) Максвелла описывается следующей системой уравнений, справедливых для любого твердого тела:
Первое из уравнений описывает поступательное движение центра масс (тела) под действием приложенных к телу внешних сил, результирующая которых и записана в правой части уравнения (1). Второе уравнение называется уравнением моментов, может быть записано относительно произвольного начала (как неподвижного, так и движущегося). Запись уравнения (2) относительно неподвижного начала может оказаться весьма неудобной, ведь законы движения точек приложения сил, вызывающих моменты, до решения системы (1)-(2) неизвестны. Поэтому начало (относительно которого считаются моменты) удобно жестко связать с движущимся телом, т.е. выбрать начало в системе отсчета, движущейся вместе с телом (т.е. с центром масс тела). Но центр масс тела движется ускоренно, вследствие чего связанная с ним система отсчета неинерциальна. Поэтому при произвольном выборе начала (жестко связанного с движущимся телом) в правой части уравнения (2) должны, появиться в качестве слагаемых моменты сил инерции (появление которых связано с движущейся системой отсчета). Однако, если в качестве начала выбрать центр масс тела, то суммарный момент сил инерции (относительно центра масс) обратиться в нуль. Тогда в правой части уравнения (2) под Так как движение маятника Максвелла - плоское (каждая точка маятника движется в вертикальной плоскости), то второе уравнение упрощается и принимает вид:
где L - проекция момента импульса, а M - проекция момента внешних сил на ось маятника. Так как при вращении относительно оси, не меняющей своего направления (в частности, неподвижной), имеет место соотношение:
где I - момент инерции тела относительно упомянутой оси, w - угловая скорость вращения (относительно этой же оси). На основании (3), (4) можно записать:
В последней формуле ε представляет собой угловое ускорение вращающегося тела. Так как центр масс маятника движется вдоль одного направления (поднимается или опускается), то уравнение (1) тоже упрощается: ma = F, (6)
где а - означает проекцию ускорения тела, а F - проекцию суммы внешних сил на вертикальное направление. Таким образом, система уравнений (1) - (2) принимает вид: I·e = M, m×a = F. Решая эти уравнения можно определить закон движения маятника. Если же ускорение маятника известно, то можно найти момент инерции (маятника) относительно его оси. Последнее и является целью настоящей работы, когда по измеряемым величинам вычисляется ускорение, а после чего находится момент инерции I.
ma = mg - T. (7) Относительно оси маятника моментом обладает только сила натяжения нити: M = T·R = т.е. R - половина внешнего диаметра d оси маятника (толщиной намотанной нити пренебрегаем). С учетом (8) уравнение (5) принимает вид: I·e = T·R. (9) a = e·R. (10) Исключая T, e из (7), (9), (10), можно получить:
Так как движение маятника вниз - равноускоренное, то
где h - первоначальная высота подъема маятника. Подстановка (12) в (11) позволяет получить окончательную формулу:
Кинетическая энергия плоского движения твердого тела [2] равна
где v - скорость центра масс, I - момент инерции тела относительно оси, проходящей через его центр масс. Пренебрегая силами сопротивления, можно получить формулу (13) с помощью закона сохранения механической энергии, приравнивая механические энергии маятника в начальном и конечном положениях, например, для движения вниз
и учитывая, что в отсутствие проскальзывания нити
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.217.176 (0.009 с.) |

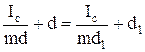 . (23)
. (23)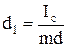 . (24)
. (24)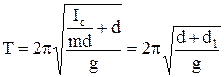 . (25)
. (25) , (26)
, (26) . (27)
. (27) . (28)
. (28)

 .
.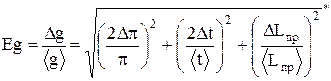 *, (29)
*, (29)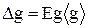 . (30)
. (30) (31)
(31)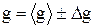 м/с2, Еg= %, a=0,9; ta,n-1 = 2,1 (32)
м/с2, Еg= %, a=0,9; ta,n-1 = 2,1 (32) .
. 11. Дайте определение физического маятника. Каковы свойства центра качаниий оборотного маятника.
11. Дайте определение физического маятника. Каковы свойства центра качаниий оборотного маятника. 15. Определите положение центра масс (т.С) относительно выбранного начала отсчета (т.О), если m1 = 2кг, m2 = 3кг, L = 1м (расстояние между m1 и m2).
15. Определите положение центра масс (т.С) относительно выбранного начала отсчета (т.О), если m1 = 2кг, m2 = 3кг, L = 1м (расстояние между m1 и m2). , (1)
, (1) . (2)
. (2) понимается суммарный момент (относительно центра масс) всех внешних сил, действующих на тело, а под
понимается суммарный момент (относительно центра масс) всех внешних сил, действующих на тело, а под 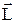 в левой части - момент импульса твердого тела при его вращении относительно оси, проходящей через центр масс.
в левой части - момент импульса твердого тела при его вращении относительно оси, проходящей через центр масс. , (3)
, (3) , (4)
, (4) , (5)
, (5) . (5а)
. (5а) , (6a)
, (6a) Внешними силами, действующими на маятник, является сила тяжести mg и суммарная сила натяжения нитей Т (см. рис.28). Принимая за положительное направление вертикали направление вниз, можно переписать уравнение (6) в виде:
Внешними силами, действующими на маятник, является сила тяжести mg и суммарная сила натяжения нитей Т (см. рис.28). Принимая за положительное направление вертикали направление вниз, можно переписать уравнение (6) в виде: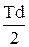 , (8)
, (8)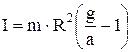 . (11)
. (11)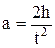 , (12)
, (12) . (13)
. (13)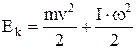 ,
,
 , а для ускоренного движения маятника вниз высота h связана с конечной скоростью v формулой
, а для ускоренного движения маятника вниз высота h связана с конечной скоростью v формулой  .
.


