
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И определение угловой скорости прецессии гироскопаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте ЦЕЛЬ РАБОТЫ Изучение динамики вращательного движения, закона сохранения момента импульса на примере вращения гироскопа. Ознакомление с гироскопическим эффектом и определение угловой скорости прецессии гироскопа.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Гироскопические приборы и системы применяются в различных областях техники: в авиации и на морских судах; в горнорудной и нефтяной промышленности (при прокладке шахт, тоннелей, при бурении скважин); в артиллерии и на танках для стабилизации прицелов и орудий и т.д. В частности, успехи в области авиационной и ракетной техники стали возможными благодаря автоматизации процессов управления летательными аппаратами. С помощью гироскопических приборов и систем решаются как задачи по управлению, ориентации, автономной навигации летательных объектов, так и проблемы по стабилизации и управлению специальных бортовых систем (антенны бортовых радиолокационных станций, чувствительные элементы головок самонаведения реактивных снарядов, авиационные прицелы и др.) Гироскопические приборы и системы по назначению делятся на несколько групп. Применительно к теме данной лабораторной работы в гироскопических стабилизаторах используется свойство гироскопа сохранять неизменным направление своей оси вращения в пространстве. Гироскоп - быстро вращающееся симметричное твердое тело, ось вращения которого может изменять своё направление в пространстве. Необычные свойства гироскопа проявляются при выполнении следующих условий. Во-первых, ось вращения гироскопа должна иметь возможность изменять своё направление в пространстве и, во-вторых, угловая скорость вращения гироскопа вокруг своей оси должна быть значительно больше угловой скорости, которую будет иметь сама ось при изменении своего направления. Наибольшее применение имеют симметричные гироскопы, которые обладают осью симметрии, являющейся свободной осью вращения. Свободными осями тела называются такие оси вращения, которые сами (без воздействия внешних сил) могут сохранять неизменными своё направление в пространстве. Эти оси называются также главными осями инерции тела. В теле произвольной формы всегда существуют три взаимно - перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями вращения. Отличительной особенностью свободных осей является то, что при вращении твердого тела вокруг любой из них момент импульса ( Следует отметить, что в общем случае направление векторов Вся теория гироскопа построена на уравнении моментов (втором законе динамики для вращательного движения), согласно которому производная момента импульса твёрдого тела по времени равна результирующему моменту внешних сил, действующих на тело
причём моменты
На волчок действует момент силы тяжести, стремящейся опрокинуть волчок, равный
где d = ОС - расстояние от точки опоры до центра масс волчка;
Вектор момента Согласно (1) за время dt момент импульса волчка получит приращение, равное
в результате чего плоскость ОО1А, в которой расположены ось волчка и вектор
Следует подчеркнуть, что вектор приращения момента импульса Следовательно, вектор момента импульса Итак, волчок-гироскоп будет прецессировать вокруг вертикальной оси Z с угловой скоростью Из рис. 32 следует, что
Учитывая, что величина момента импульса волчка-гироскопа равна
где I - момент инерции волчка-гироскопа; m - масса волчка (вместе с осью). Из (6) видно, что угловая скорость прецессии ( Следует отметить, что прецессионное движение имеет следующие особенности. Во-первых, угловая скорость прецессии значительно меньше угловой скорости вращения гироскопа вокруг собственной оси, т.е. Во-вторых, из выражения
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1944; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

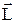 ) совпадает по направлению с угловой скоростью (
) совпадает по направлению с угловой скоростью ( ).
). не совпадают.
не совпадают. , (1)
, (1) определены относительно одной и той же точки заданной системы отсчёта (относительно неподвижной точки опоры гироскопа).
определены относительно одной и той же точки заданной системы отсчёта (относительно неподвижной точки опоры гироскопа). Рассмотрим поведение гироскопа на примере волчка с неподвижной точкой опоры О (рис. 32). Оказалось, что если ось вращающегося волчка наклонена к вертикали, то она (ось) описывает конус вокруг вертикали (оси Z) с угловой скоростью
Рассмотрим поведение гироскопа на примере волчка с неподвижной точкой опоры О (рис. 32). Оказалось, что если ось вращающегося волчка наклонена к вертикали, то она (ось) описывает конус вокруг вертикали (оси Z) с угловой скоростью  . Указанное движение оси волчка - гироскопа называется прецессионным (прецессией), при котором ось волчка остаётся на поверхности конуса с вершиной в точке О и вместе с осью совершает движение вектор момента импульса
. Указанное движение оси волчка - гироскопа называется прецессионным (прецессией), при котором ось волчка остаётся на поверхности конуса с вершиной в точке О и вместе с осью совершает движение вектор момента импульса  ) вращения волчка вокруг собственной оси, тем больше угловая скорость прецессии (
) вращения волчка вокруг собственной оси, тем больше угловая скорость прецессии (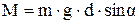 , (2)
, (2)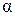 - угол, образованный осью волчка (гироскопа) с вертикалью (осью Z).
- угол, образованный осью волчка (гироскопа) с вертикалью (осью Z). перпендикулярен к плоскости ОО1А, в которой находится сила тяжести
перпендикулярен к плоскости ОО1А, в которой находится сила тяжести  .
. (3)
(3)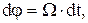 . (4)
. (4) сонаправлен с вектором
сонаправлен с вектором  .
.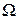 прецессии, определяемой следующим образом.
прецессии, определяемой следующим образом. . (5)
. (5) * и, подставляя (2) в (5), получим согласно (4) выражение для вычисления угловой скорости прецессии:
* и, подставляя (2) в (5), получим согласно (4) выражение для вычисления угловой скорости прецессии: ,
,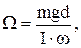 (6)
(6) ) волчка, тем больше угловая скорость прецессии (
) волчка, тем больше угловая скорость прецессии ( .
. ] следует, что момент (
] следует, что момент ( ) определяет угловую скорость прецессии (
) определяет угловую скорость прецессии ( ), а не угловое ускорение. Следовательно, устранение момента
), а не угловое ускорение. Следовательно, устранение момента 


