
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила проявления гироскопических эффектовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Правило прецессии В силу общего закона динамики вращательного движения (
где: Как было показано выше, движение с угловой скоростью прецессии происходит таким образом, чтобы совместить вектор 15.1.4.2 Правило гироскопической реакции При действии на гироскоп, обладающий кинетическим моментом
где: а вектор момента гироскопической пары направлен так, что
Направление гироскопических сил можно ищется с помощью правила Н.Е. Жуковского: гироскопический момент реакции стремится совместить вектор Следовательно, можно сформулировать следующий вывод. При действии на гироскоп с кинетическим моментом первый – вызывает вынужденную прецессию (при наличии необходимой степени свободы) с угловой скоростью: второй - уравновешивает внешний момент
15.1.4 Порядок формирования гироскопических моментов Последовательность формирования этих гироскопических моментов демонстрируется на рис. 15.6, где приняты следующие обозначения:
Рис. 15.6
- СК - СК - - - - - - - - - Действие внешнего момента Действие внешнего момента Причинно-следственная последовательность физических явлений по рис. 15.6 выглядит следующим образом:
Даже очень небольшой момент управления
15.1.5 Акселерометр Акселерометр (датчик линейного ускорения подвижного объекта) является механическим прибором с одной степенью свободы, содержащим чувствительную массу, перемещение которой под действием сил инерции относительно корпуса прибора ограничено упругой связью и несёт информацию об ускорении. На рис. 15.8 показана простейшая схема осевого акселерометра.
Рис. 15.8 Корпус 1 акселерометра связан с подвижным объектом 2 через упругий подвес 3. Ось Х, вдоль которой перемещается под действием сил инерции груз 2, является осью чувствительности. Перемещение х груза 2 вдоль оси Х измеряется с помощью датчика 4 линейных перемещений; демпфирование собственных колебаний груза 2 осуществляется демпфером 5. Если акселерометр установить на ЛА, вектор линейного ускорения
Рис. 15.9
К чувствительному элементу акселерометра (груз 2) приложены следующие силы (после окончания переходных процессов): ‒ сила инерции ‒ упругая сила ‒ составляющая силы тяжести С учетом направлений векторов сил можно записать следующее скалярное уравнение баланса сил для установившегося режима:
откуда следует, что перемещение
Величина В дальнейшем будем обозначать В переходных режимах на тело 2 дополнительно действует демпфирующая сила Движение груза 2 состоит из переносного движения вместе с корпусом 1 и из относительного движения по отношению к этому корпусу (второй закон Ньютона без учета трения): В результате можно записать (
где:
Последнее выражение можно записать в виде:
При
Следовательно, акселерометр измеряет величину Для объекта, который находится в покое или движется прямолинейно и равномерно (
которое является основой для построения акселерометрических датчиков абсолютного угла. Типы гироскопов
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 , т.е. изменение главного кинетического момента
, т.е. изменение главного кинетического момента  определяется выражением
определяется выражением  ) любой внешний момент, вектор которого не совпадает по направлению с вектором
) любой внешний момент, вектор которого не совпадает по направлению с вектором  , изменяет положение вектора главного кинетического момента гироскопа
, изменяет положение вектора главного кинетического момента гироскопа  ,
, - проекция вектора внешнего момента на экваториальную плоскость ротора гироскопа (плоскость, проходящая через точу
- проекция вектора внешнего момента на экваториальную плоскость ротора гироскопа (плоскость, проходящая через точу  и перпендикулярная вектору
и перпендикулярная вектору 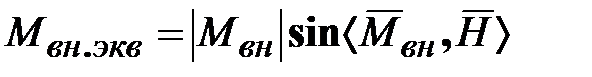 .
. по кратчайшему пути.
по кратчайшему пути. возникает момент гироскопической реакции:
возникает момент гироскопической реакции: ,
, ,
, совмещает по кратчайшему пути вектор
совмещает по кратчайшему пути вектор  ) с вектором
) с вектором  :
: .
. , вектор которого не совпадает по направлению с вектором
, вектор которого не совпадает по направлению с вектором 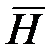 , возникают два гироскопических момента:
, возникают два гироскопических момента: в направлении совмещения по кратчайшему пути вектора
в направлении совмещения по кратчайшему пути вектора  с вектором
с вектором  ;
; .
.
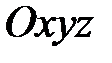 соответствует исходному (нулевому) положению осей карданова подвеса;
соответствует исходному (нулевому) положению осей карданова подвеса; соответствует текущему положению осей карданова подвеса;
соответствует текущему положению осей карданова подвеса; - угол поворота вокруг оси -
- угол поворота вокруг оси - 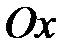 ;
; - угол поворота вокруг оси -
- угол поворота вокруг оси - 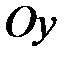 ;
; - момент гироскопический реакции, направленный вдоль оси
- момент гироскопический реакции, направленный вдоль оси  , возникающий при действии на гироскоп переносной угловой скорости
, возникающий при действии на гироскоп переносной угловой скорости  (вызывает перемещение с угловой скоростью вынужденной прецессии
(вызывает перемещение с угловой скоростью вынужденной прецессии 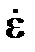 );
); - момент гироскопический реакции вдоль оси
- момент гироскопический реакции вдоль оси  при действии на гироскоп вынужденной прецессии с угловой скоростью
при действии на гироскоп вынужденной прецессии с угловой скоростью  ;
; - момент инерции подвижных частей (полезная нагрузка при использовании гироскопа в качестве гироскопического привода) относительно оси
- момент инерции подвижных частей (полезная нагрузка при использовании гироскопа в качестве гироскопического привода) относительно оси  ;
; - момент инерции подвижных частей (полезная нагрузка) относительно оси
- момент инерции подвижных частей (полезная нагрузка) относительно оси  ;
; - инерционный момент, характеризующий динамику разгона при повороте вокруг оси
- инерционный момент, характеризующий динамику разгона при повороте вокруг оси  ;
; - инерционный момент, характеризующий динамику разгона при повороте вокруг оси
- инерционный момент, характеризующий динамику разгона при повороте вокруг оси  ;
; - внешний (возмущающий или управляющий) моменты.
- внешний (возмущающий или управляющий) моменты. вдоль оси
вдоль оси  (в экваториальной плоскости
(в экваториальной плоскости  ) по второму закону Ньютона вызывает появление угловой скорости
) по второму закону Ньютона вызывает появление угловой скорости  нагрузки с моментом инерции
нагрузки с моментом инерции  , являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент
, являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент  (лежит в экваториальной плоскости, но ортогонален по отношению к моменту, его вызвавшему), направленный таким образом, чтобы по кратчайшему пути совместить вектор
(лежит в экваториальной плоскости, но ортогонален по отношению к моменту, его вызвавшему), направленный таким образом, чтобы по кратчайшему пути совместить вектор  .
. вдоль оси
вдоль оси  по второму закону Ньютона вызывает появление угловой скорости
по второму закону Ньютона вызывает появление угловой скорости  нагрузки с моментом инерции
нагрузки с моментом инерции  , являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент
, являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент  , направленный таким образом, чтобы по кратчайшему пути совместить вектор
, направленный таким образом, чтобы по кратчайшему пути совместить вектор 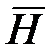 с вектором
с вектором  . Гироскопический момент
. Гироскопический момент  уравновешивает внешний момент
уравновешивает внешний момент 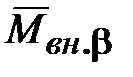 , и движение останавливается.
, и движение останавливается.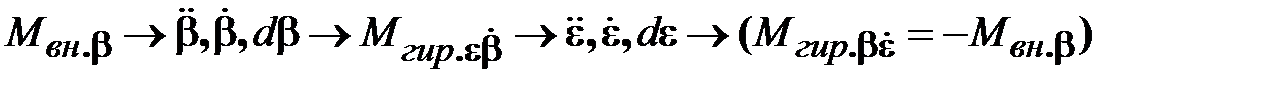 .
. , создаваемый моментным двигателем
, создаваемый моментным двигателем 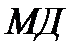 , вызывает появление значительного движущего момента относительно ортогональной оси, превышающего управляющий момент на несколько порядков. Таким образом, гироскоп может выполнять функции усилителя момента и использоваться в качестве силового гиропривода.
, вызывает появление значительного движущего момента относительно ортогональной оси, превышающего управляющий момент на несколько порядков. Таким образом, гироскоп может выполнять функции усилителя момента и использоваться в качестве силового гиропривода.
 которого расположен под углом
которого расположен под углом  к горизонту, то схема сил, действующих на акселерометр, показана на рис. 15.9.
к горизонту, то схема сил, действующих на акселерометр, показана на рис. 15.9.
 (она прикладывается к элементу связи груза 2, характеризуемого упругостью
(она прикладывается к элементу связи груза 2, характеризуемого упругостью  );
); деформации пружины;
деформации пружины; вдоль оси чувствительности акселерометра.
вдоль оси чувствительности акселерометра. ,
, массы 2 равно:
массы 2 равно: . (15.6)
. (15.6) называется «кажущимся» ускорением, статический коэффициент перед которым является характеристикой чувствительности акселерометра.
называется «кажущимся» ускорением, статический коэффициент перед которым является характеристикой чувствительности акселерометра. и
и  .
.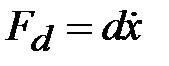 вдоль оси чувствительности акселерометра.
вдоль оси чувствительности акселерометра. ):
):
 - проекция переносного ускорения на ось Х чувствительности, равного абсолютному ускорению той точки корпуса 1 акселерометра, с которой в данный момент времени совпадает центр масс груза 2 (при малых размерах акселерометра переносное ускорение
- проекция переносного ускорения на ось Х чувствительности, равного абсолютному ускорению той точки корпуса 1 акселерометра, с которой в данный момент времени совпадает центр масс груза 2 (при малых размерах акселерометра переносное ускорение  можно принять равным абсолютному ускорению центральной точки корпуса 1 акселерометра);
можно принять равным абсолютному ускорению центральной точки корпуса 1 акселерометра); - относительное ускорение, равное ускорению центра масс груза 2 относительно корпуса 4 акселерометра.
- относительное ускорение, равное ускорению центра масс груза 2 относительно корпуса 4 акселерометра. . (15.7)
. (15.7) получается уравнение относительно равновесия для груза 2:
получается уравнение относительно равновесия для груза 2: .
. .
. ) можно записать следующее соотношение:
) можно записать следующее соотношение: ,
,


