
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обеспечение максимальной динамической точности многоканальной СН комбинированного управления с компенсирующей связьюСодержание книги
Поиск на нашем сайте
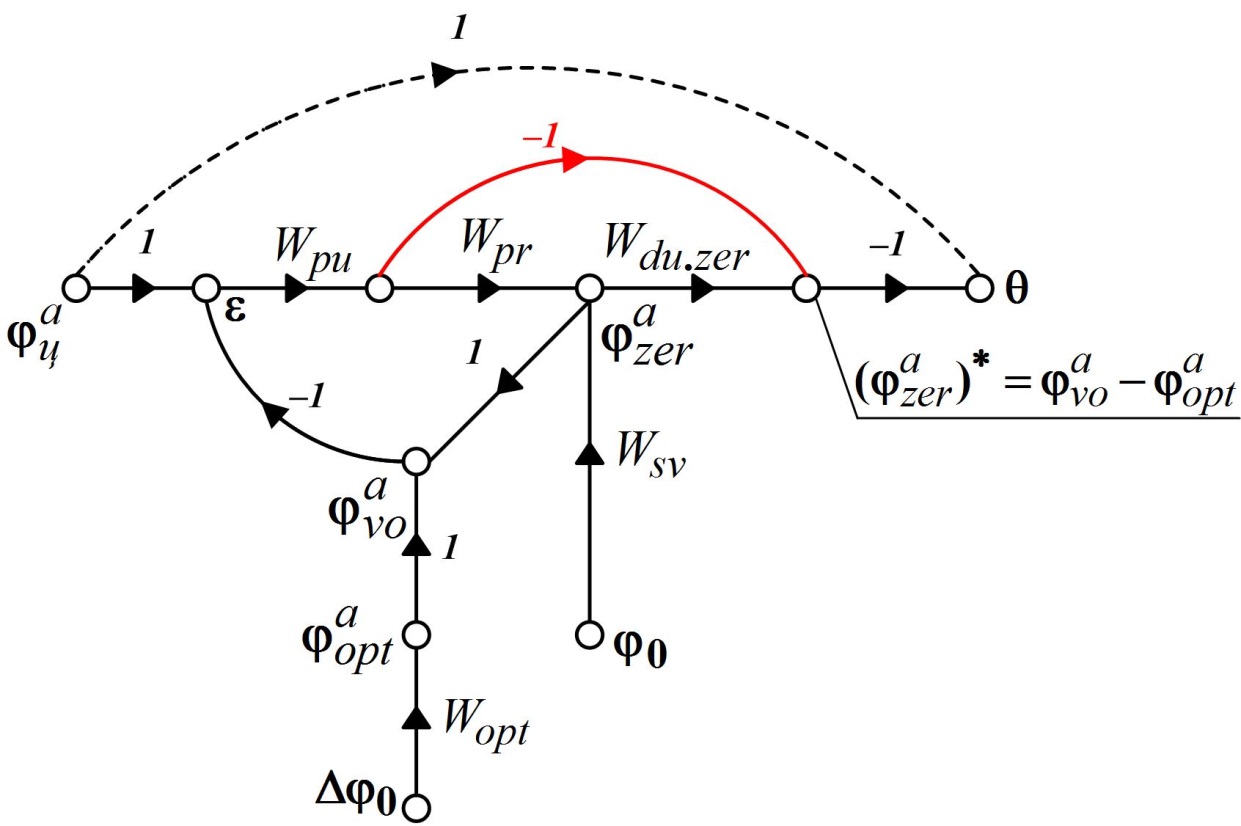
Для улучшения динамической точности двухканальной СН со структурой по рис. 13.10 следует стремиться к выполнению условий (12.26) и (13.6). Будем рассматривать два привода, суммирование выходных угловых координат которых происходит по принципу разделенной нагрузки. При этом построение этих приводов соответствует структуре по рис. 12.11. Разомкнутая часть таких приводов показана на рис. 13.11. В этом случае могут быть получены следующие соотношения:
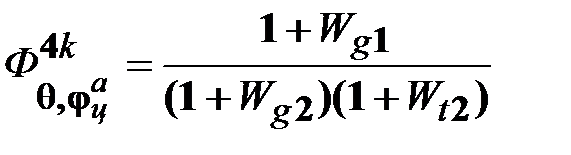 ; ;
13.7.1 Обеспечение условия Одним из вариантов выполнения условия Ещё одним вариантом выполнения условия уменьшения влияния
Рис. 13.12
Для данной структуры запишем выражения для ПФ по ошибке:
Раздел 14 ОСОБЕННОСТИ АППАРАТУРНОЙ РЕАЛИЗАЦИИ БОРТОВОЙ СН – ОПТИЧЕСКИЙ ПЕЛЕНГАТОР
Динамические характеристики оптического пеленгатора
Особенностями оптического пеленгатора рассматриваемой СН (рис. 14.1) являются высокие требования к точности измерения, протяженный характер размещения оптико-механического тракта (ОМТ). Особенностью такого ОМТ являются флуктуации его оптической оси (угол
Рис. 14.1
В этом случае поворот зеркала для минимизации угла рассогласования Следовательно, измерение угла поворота зеркала
Рис. 14.2
Ошибка измерения входного воздействия ‒ в случае отсутствия компенсирующей связи
‒ в случае наличия компенсирующей связи (выделена красным цветом)
Следовательно, для компенсации воздействия вибрации ЛА на оптику пеленгатора полезнее формировать компенсирующую связь со знаком «минус» (следует отметить, что полезный эффект в этом случае не велик), а для компенсации качки ЛА ‒ со знаком «плюс»
Раздел 15 ОСОБЕННОСТИ АППАРАТУРНОЙ РЕАЛИЗАЦИИ БОРТОВОЙ СН – ГИРОСКОПИЧЕСКИЕ ПРИБОРЫ
Гироскоп
Гироскопом (симметрическим гироскопом) называется твердое тело, вращающееся вокруг неподвижной точки Гироскоп называется уравновешенным, если точка
Рис. 15.1 В гироскопических приборах ротор гироскопа обычно закрепляют в кардановом подвесе, позволяющем ротору совершить любой поворот вокруг неподвижного центра подвеса, совпадающего с центром масс (ЦМ) ротора гироскопа (имеется три степени свободы). Карданов подвес - универсальная шарнирная опора, позволяющая закреплённому в ней объекту вращаться одновременно в нескольких плоскостях. Основная идея карданова подвеса: несколько колец, расположенных одно внутри другого, соединяются в двух противоположных точках, что дает им возможность вращаться относительно друг друга. Если в центре колец поместить груз, то он будет сохранять вертикальное положение. Какие бы движения ни совершали кольца, груз останется неподвижной, поскольку кольца гасят колебания. Если в кардановом подвесе закрепить вращающееся тело, то оно будет сохранять направление оси вращения независимо от ориентации самого подвеса. Карданов подвес обеспечивает вращающемуся телу свободный поворот в пространстве вокруг трех взаимно перпендикулярных осей, пересекающихся в одной точке, называемой точкой подвеса. Эта точка при любых указанных поворотах остается неподвижной (рис. 15.2).
Точка подвеса Рис. 15.2
15.1.1 Элементарная (прецессионная) теория гироскопов ( В общем случае кроме угловой скорости В каждый момент времени абсолютная угловая скорость гироскопа: В этом случае кинетический момент В общем случае можно записать:
где полагаем, что ось
Для уравновешенного гироскопа с точкой закрепления центра масс (свободный гироскоп), если пренебречь трением, можно записать Пусть на ось гироскопа через опору действует сила
где: - вектор Учитывая, что производная от вектора
Рис. 15.3
Данное равенство соответствует теоремеРезаля: скорость конца вектора кинетического момента тела (гироскопа) относительно центра Следовательно, точка Из равенства (15.1) следует, что когда действие силы прекратится, то
Прецессия Допустим, что сила Так как ось
и из равенства (15.1) получается:
Уравнение (15.2) является исходным приближенным уравнением элементарной (прецессионной) теории гироскопа (в элементарной теории гироскопа нутация не учитывается). Из уравнения (15.2) следует:
Чем больше
Гироскопический эффект Пусть гироскоп имеет только две степени свободы: поворот вокруг оси
Рис. 15.4
Пусть основание 1 вращается вокруг оси Но, когда подшипники действуют на ось ротора с силами Пара сил Поскольку момент
Правило Н.Е. Жуковского: если быстро вращающемуся гироскопу сообщить вынужденное прецессионное движение, то на подшипники, в которых закреплена ось ротора гироскопа, начнет действовать гироскопическая пара с моментом Под действием гироскопической пары кольцо 2 начнет вращаться вместе с ротором вокруг оси
|
|||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.165.192 (0.011 с.) |

 .
.
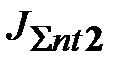 ), применение в этом канале низковольтных двигателей (уменьшение
), применение в этом канале низковольтных двигателей (уменьшение 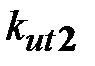 ), увеличение значений движущих моментов грубого канала (
), увеличение значений движущих моментов грубого канала (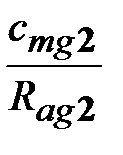 ).
).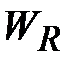 на динамическую точность СП ППУ является построение двухканального СП ППУ по структуре двухканального итеративного СП (рис. 12.16), так как в этом случае увеличивается модуль знаменателя ПФ
на динамическую точность СП ППУ является построение двухканального СП ППУ по структуре двухканального итеративного СП (рис. 12.16), так как в этом случае увеличивается модуль знаменателя ПФ 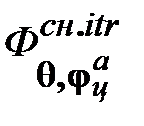 и
и 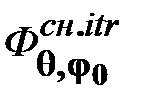 . В этом случае структура двухканальной СН комбинированного управления принимает вид, как показано на рис. 13.12.
. В этом случае структура двухканальной СН комбинированного управления принимает вид, как показано на рис. 13.12.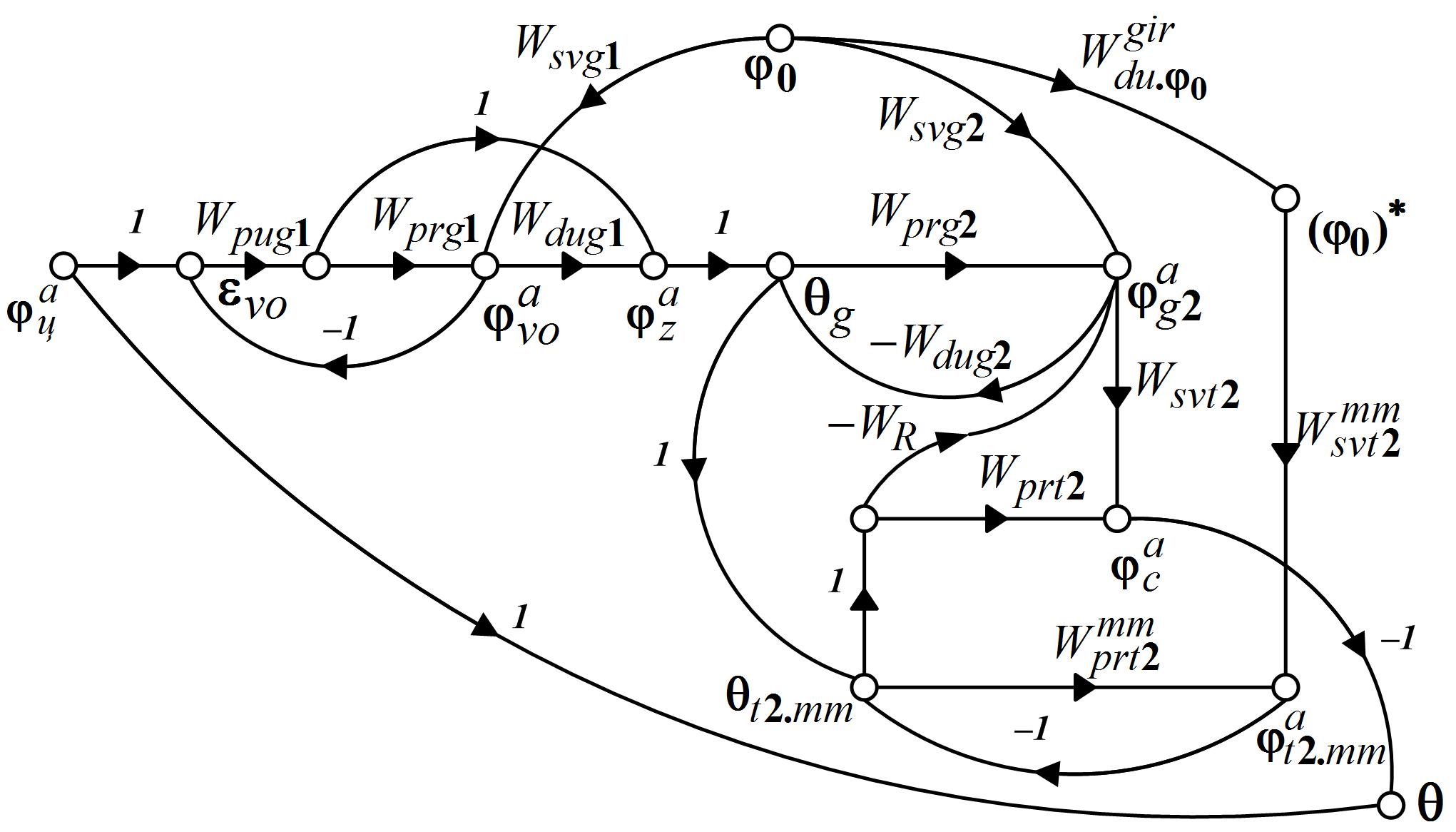
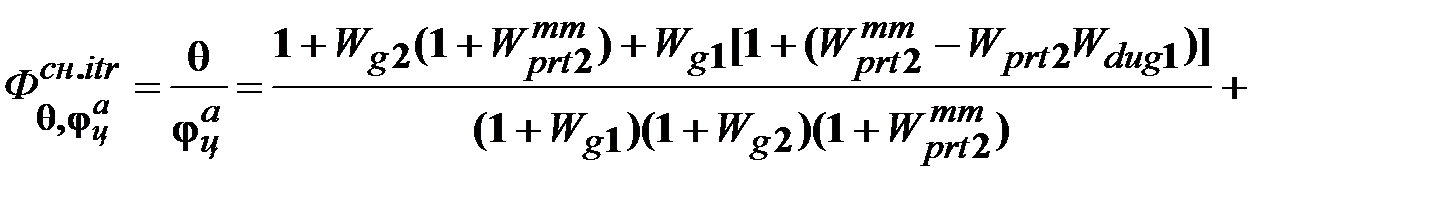
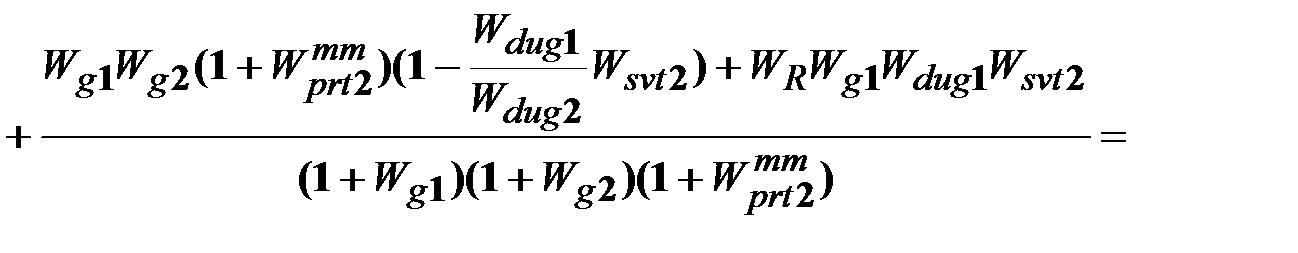
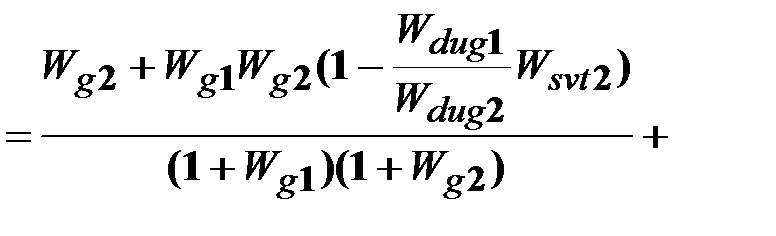
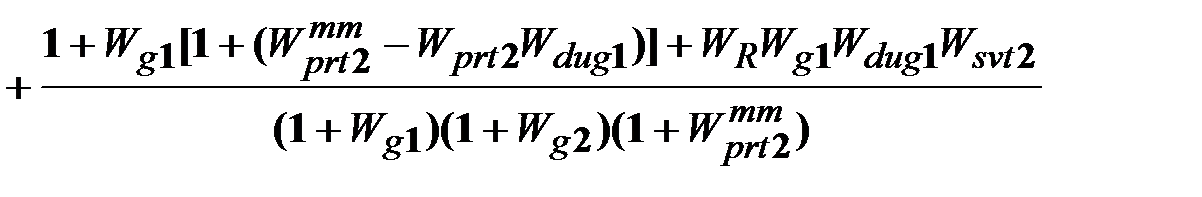 . (13.18)
. (13.18)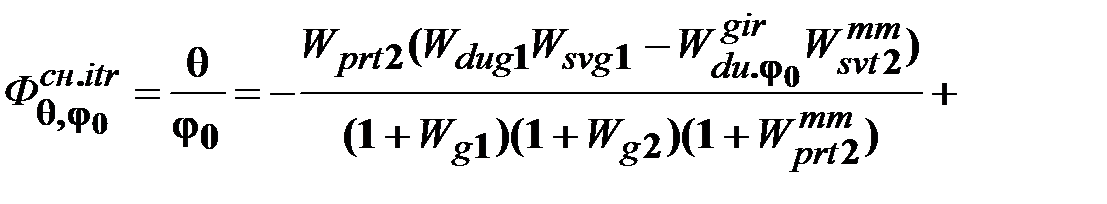
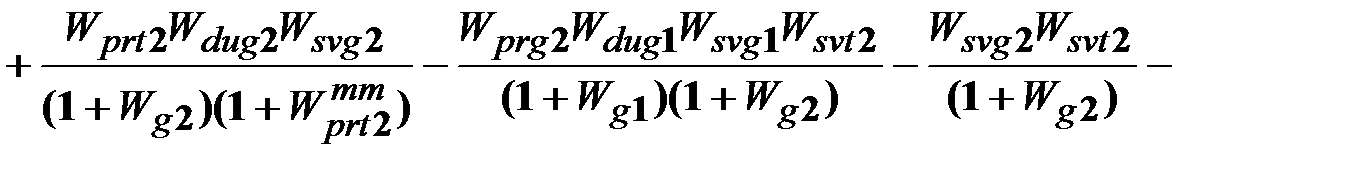
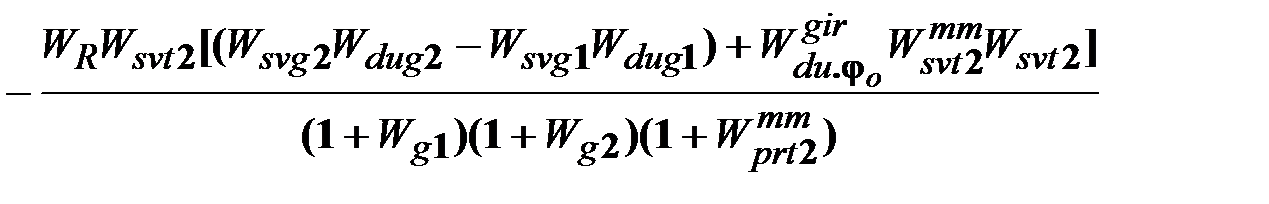 . (13.19)
. (13.19)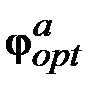 ) вследствие упругих конструктивных колебаний элементов оптической схемы. Если считать в соответствии с рис. 14.1, что положение оптической оси ОМТ в невозмущенном состоянии и при нулевом положении сканирующего зеркала ОМТ совпадает с направлением
) вследствие упругих конструктивных колебаний элементов оптической схемы. Если считать в соответствии с рис. 14.1, что положение оптической оси ОМТ в невозмущенном состоянии и при нулевом положении сканирующего зеркала ОМТ совпадает с направлением 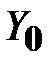 , то только за счет вибрационных эффектов оптическая ось занимает положение, отмеченной на рис. 14.1 зеленой штрих пунктирной линией.
, то только за счет вибрационных эффектов оптическая ось занимает положение, отмеченной на рис. 14.1 зеленой штрих пунктирной линией.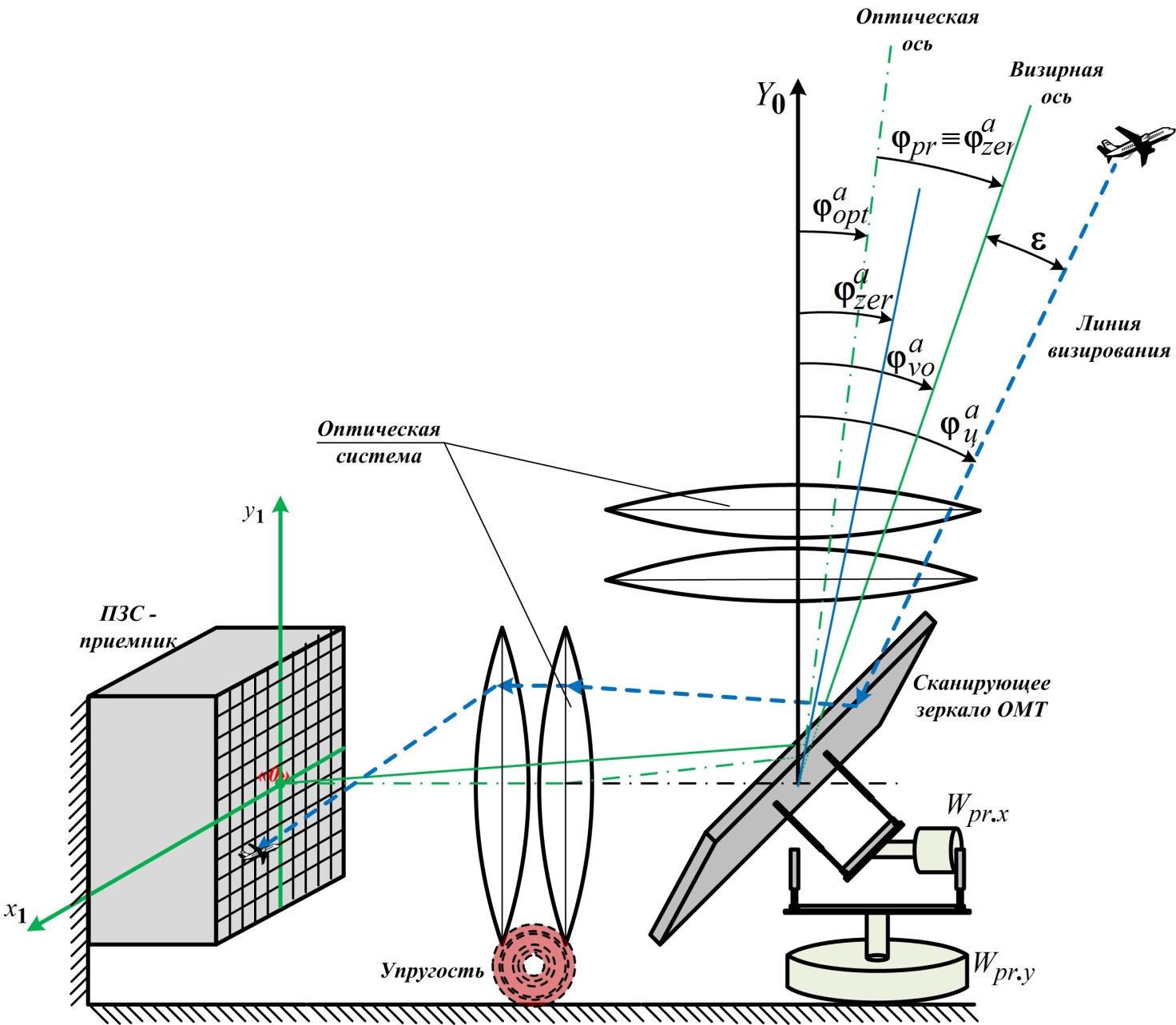
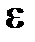 будет совершаться на угол
будет совершаться на угол  , меньший, чем угол
, меньший, чем угол 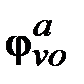 , на величину
, на величину 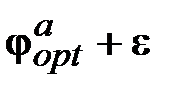 .
.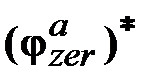 с помощью гироскопических датчиков не является измерением (с ошибкой
с помощью гироскопических датчиков не является измерением (с ошибкой 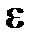 ) положения визирной оси
) положения визирной оси 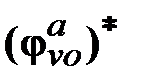 , как это показано на рис. 14.2. Кроме того, возникает необходимость фильтрации получаемых измерений углового рассогласования
, как это показано на рис. 14.2. Кроме того, возникает необходимость фильтрации получаемых измерений углового рассогласования  .
.
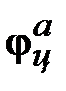 , определяемая вибрацией
, определяемая вибрацией 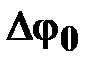 , может быть рассчитана по следующим ПФ:
, может быть рассчитана по следующим ПФ: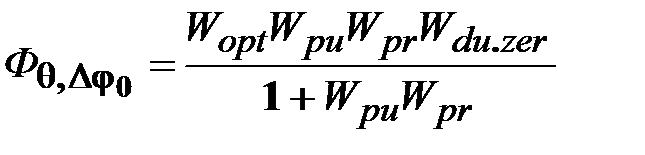 ;
;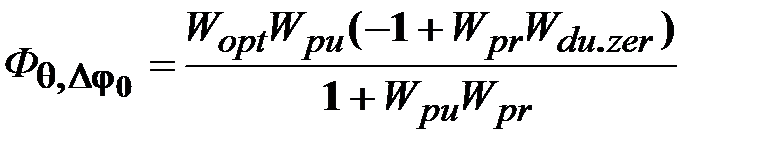 .
. и обладающее осью
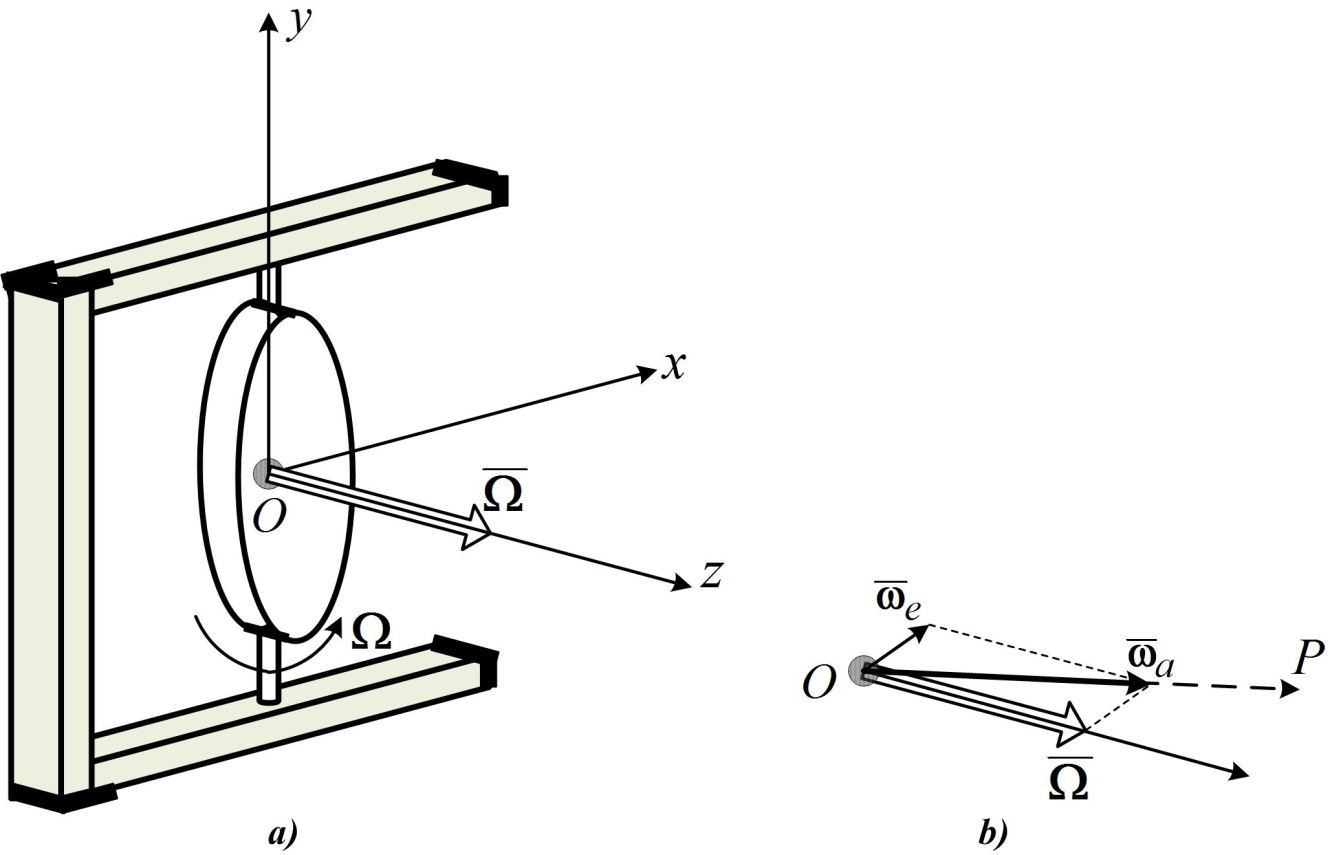
и обладающее осью 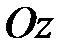 динамической симметрии (главная центральная ось инерции), которая проходит через центр инерции (масс) гироскопа (рис. 15.1 а).
динамической симметрии (главная центральная ось инерции), которая проходит через центр инерции (масс) гироскопа (рис. 15.1 а).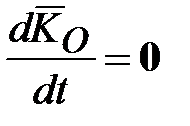 , где
, где 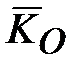 - кинетический момент, что следует из теоремы моментов относительно неподвижного центра:
- кинетический момент, что следует из теоремы моментов относительно неподвижного центра: 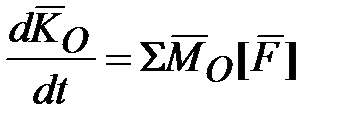 ).
).

 >>
>> 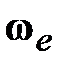 )
) вращения твердого массивного тела вокруг оси
вращения твердого массивного тела вокруг оси  поворота оси
поворота оси 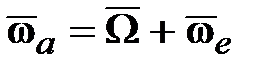 . Его суммарный поворот вокруг неподвижной точки
. Его суммарный поворот вокруг неподвижной точки 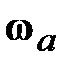 вокруг мгновенных осей вращения
вокруг мгновенных осей вращения 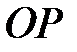 . При выполнении условия
. При выполнении условия  >>
>> 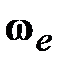 угол
угол 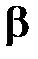 (рис. 15.1 b) очень мал и можно принять
(рис. 15.1 b) очень мал и можно принять 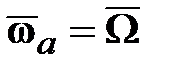 , а ось
, а ось 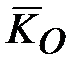 гироскопа относительно точки
гироскопа относительно точки 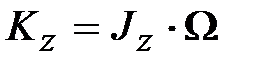 (основное допущение элементарной теории гироскопа).
(основное допущение элементарной теории гироскопа).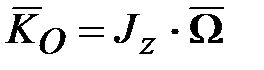 ,
,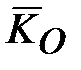 все время направлены вдоль одной и той же прямой;
все время направлены вдоль одной и той же прямой;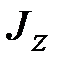 ‒ момент инерции гироскопа относительно оси
‒ момент инерции гироскопа относительно оси 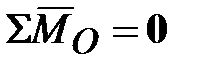 (
(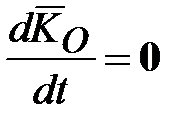 ) и
) и 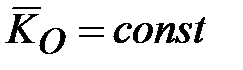 . Следовательно, ось свободного гироскопа сохраняет неизменное направление в пространстве по отношению к инерциальной (абсолютной) СК.
. Следовательно, ось свободного гироскопа сохраняет неизменное направление в пространстве по отношению к инерциальной (абсолютной) СК.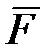 (рис. 15.3), момент которой относительно центра масс
(рис. 15.3), момент которой относительно центра масс 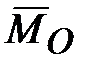 (или действует пара сил
(или действует пара сил 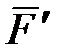 с моментом, равным
с моментом, равным 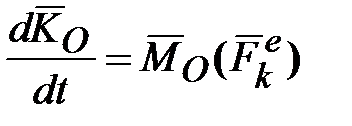 , где
, где 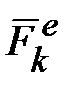 - равнодействующая всех внешних сил, действующих на данную систему):
- равнодействующая всех внешних сил, действующих на данную систему):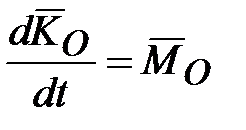 или
или 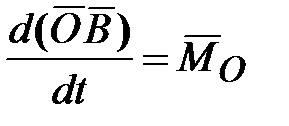 ,
,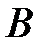 - точка оси
- точка оси 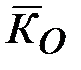 ;
;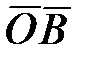 совпадает с вектором
совпадает с вектором 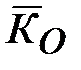 .
.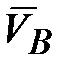 точки
точки 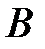 , получаем:
, получаем: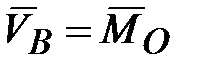 (
(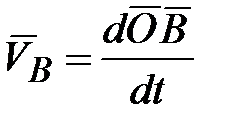 ). (15.1)
). (15.1)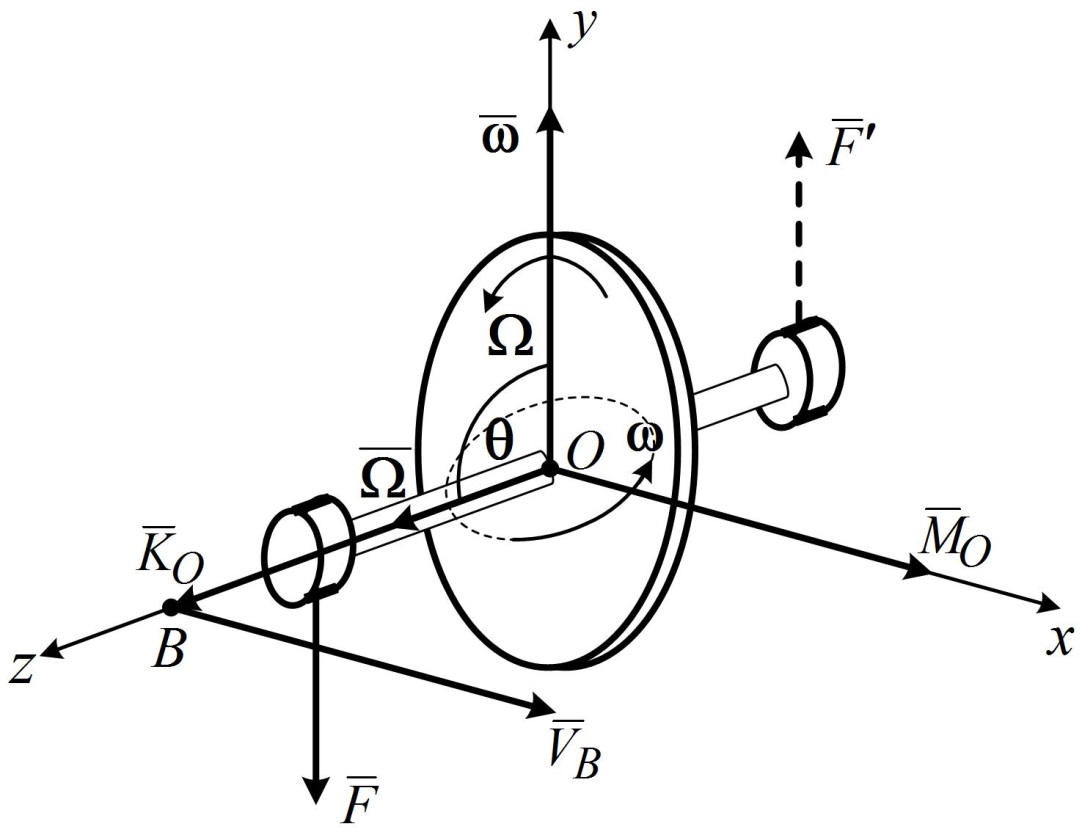
 равняется по модулю и по направлению главному моменту внешних сил относительно того же центра.
равняется по модулю и по направлению главному моменту внешних сил относительно того же центра.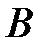 , а с нею и главная ось гироскопа, будет перемещаться по направлению вектора
, а с нею и главная ось гироскопа, будет перемещаться по направлению вектора 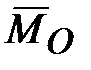 . Т.е., если на ось быстро вращающегося гироскопа подействует сила, то ось начнет отклоняться не в сторону действия силы, а по направлению, которое имеет вектор
. Т.е., если на ось быстро вращающегося гироскопа подействует сила, то ось начнет отклоняться не в сторону действия силы, а по направлению, которое имеет вектор 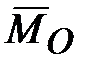 момента этой силы относительно неподвижной точки
момента этой силы относительно неподвижной точки  гироскопа (перпендикулярно этой силе).
гироскопа (перпендикулярно этой силе).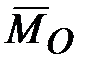 обращается в нуль и, следовательно,
обращается в нуль и, следовательно, 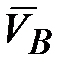 также обращается в нуль, и ось гироскопа останавливается. Таким образом, гироскоп не сохраняет движения, сообщенного ему силой. Если действие силы является кратковременным (толчок), то ось гироскопа практически не изменит своего направления (точнее ось начнет совершать вблизи начального положения высокочастотные колебания малой амплитуды - нутация, которые при наличии сопротивления затухнут, и ось придет в положение, близкое к своему начальному) - это проявление устойчивости оси быстро вращающегося гироскопа.
также обращается в нуль, и ось гироскопа останавливается. Таким образом, гироскоп не сохраняет движения, сообщенного ему силой. Если действие силы является кратковременным (толчок), то ось гироскопа практически не изменит своего направления (точнее ось начнет совершать вблизи начального положения высокочастотные колебания малой амплитуды - нутация, которые при наличии сопротивления затухнут, и ось придет в положение, близкое к своему начальному) - это проявление устойчивости оси быстро вращающегося гироскопа.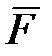 или пара сил
или пара сил 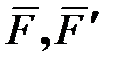 (рис. 15.3) действует на гироскоп во все время его работы, постоянно оставаясь в плоскости
(рис. 15.3) действует на гироскоп во все время его работы, постоянно оставаясь в плоскости 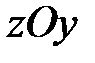 (к примеру, это могла бы быть сила тяжести). Выше мы отметили, что ось
(к примеру, это могла бы быть сила тяжести). Выше мы отметили, что ось 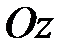 в сторону действия силы не отклоняется, поэтому угол
в сторону действия силы не отклоняется, поэтому угол 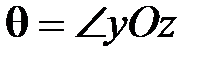 остаётся всё время постоянным, а скорость
остаётся всё время постоянным, а скорость  - перпендикулярной плоскости
- перпендикулярной плоскости 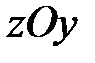 . Следовательно, ось гироскопа будет вращаться (прецессировать) вокруг оси
. Следовательно, ось гироскопа будет вращаться (прецессировать) вокруг оси 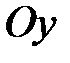 с некоторой угловой скорость
с некоторой угловой скорость 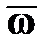 , называемой угловой скоростью прецессии.
, называемой угловой скоростью прецессии.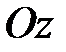 вращается вокруг оси
вращается вокруг оси  с угловой скоростью
с угловой скоростью 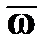 (рис. 15.3), то верна формула Эйлера
(рис. 15.3), то верна формула Эйлера 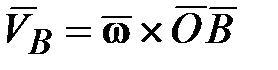 (вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки):
(вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки): ,
,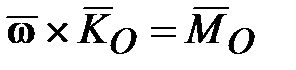 . (15.2)
. (15.2)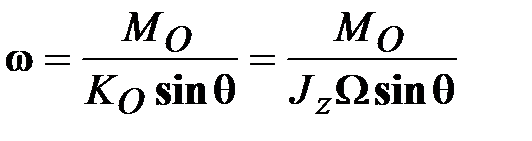 (15.3)
(15.3)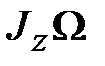 , тем меньше
, тем меньше  и тем большую точность даёт элементарная теория гироскопа.
и тем большую точность даёт элементарная теория гироскопа.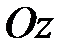 и, вместе с кольцом 2, - вокруг оси
и, вместе с кольцом 2, - вокруг оси 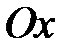 (двухстепенной гироскоп), как это показано на рис. 15.4. В этом случае, если толкнуть кольцо 2, то оно начнет свободно вращаться вокруг оси
(двухстепенной гироскоп), как это показано на рис. 15.4. В этом случае, если толкнуть кольцо 2, то оно начнет свободно вращаться вокруг оси 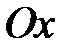 , в то время как трехстепенной гироскоп на такие толчки практически не реагирует. Не реагирует трехстепенной гироскоп и на вращение основания, сохраняя постоянным направление своей оси
, в то время как трехстепенной гироскоп на такие толчки практически не реагирует. Не реагирует трехстепенной гироскоп и на вращение основания, сохраняя постоянным направление своей оси 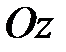 .
.
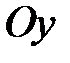 (или любой параллельной ей оси) с угловой скоростью
(или любой параллельной ей оси) с угловой скоростью 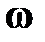 (
( >>
>> 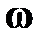 ). Вращаясь вместе с основанием, гироскоп совершает вынужденную прецессию вокруг оси
). Вращаясь вместе с основанием, гироскоп совершает вынужденную прецессию вокруг оси 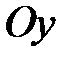 . Согласно уравнению (15.2) на ротор 3 гироскопа должен действовать момент
. Согласно уравнению (15.2) на ротор 3 гироскопа должен действовать момент 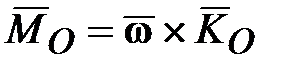 , который, очевидно, могут создать только силы
, который, очевидно, могут создать только силы 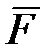 ,
, 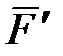 давления подшипников
давления подшипников 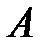 ,
, 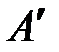 на ось ротора. Так как центр масс
на ось ротора. Так как центр масс  ротора 3 гироскопа неподвижен, то по теореме о движении центра масс (
ротора 3 гироскопа неподвижен, то по теореме о движении центра масс (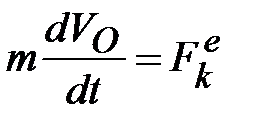 ) должно выполняться равенство
) должно выполняться равенство 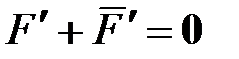 , и, следовательно, силы,
, и, следовательно, силы,  и
и 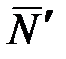 .
.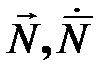 называется гироскопической парой, а её момент
называется гироскопической парой, а её момент 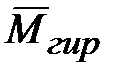 - моментом гироскопической пары или гироскопическим моментом (моментом гироскопической реакции).
- моментом гироскопической пары или гироскопическим моментом (моментом гироскопической реакции). противоположен моменту
противоположен моменту 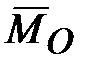 (
(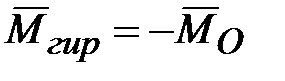 ), то:
), то: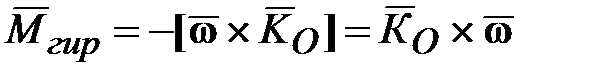 и
и . (15.4)
. (15.4) и
и 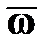 совпали.
совпали.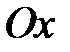 ; при этом угол
; при этом угол  , а с ним и момент
, а с ним и момент 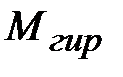 будут уменьшаться, и, когда будет выполнено равенство
будут уменьшаться, и, когда будет выполнено равенство 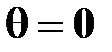 , вращение кольца 2 прекратится.
, вращение кольца 2 прекратится.


