Раздел 13 динамическая точность многоканальной комбинированной СН
Раздел 13 ДИНАМИЧЕСКАЯ ТОЧНОСТЬ МНОГОКАНАЛЬНОЙ КОМБИНИРОВАННОЙ СН
13.1 Функциональная схема двухканальной комбинированной СН при идеальном (пеленгатор) и разделенном (пушечная установка) суммировании угловых координат
Будем рассматривать следующий вариант построения структуры объединения СП (структуры СН):
‒ СП АВ представляет собой двухканальный привод комбинированного управления с идеальным суммирование выходных угловых координат локальных приводов;
‒ СП ППУ представляет собой двухканальный привод комбинированного управления с суммирование выходных угловых координат локальных приводов по принципу разделенной нагрузки.
В соответствии с материалами разделов 7, 9, 10 и 12 будем рассматривать СН, в которой каждый из следящих систем АВ и ППУ представляет собой двухканальный СП. В этом случае функциональную схему оптико-механической части многоканальной СН можно представить, как это показано на рис. 13.1, где приняты следующие обозначения:
 – пеленгационное устройство грубого канала АВ (широкое поле зрения); – пеленгационное устройство грубого канала АВ (широкое поле зрения);
 – пеленгационное устройство совокупности грубого и точного каналов АВ (узкое поле зрения); – пеленгационное устройство совокупности грубого и точного каналов АВ (узкое поле зрения);
 , ,  – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала АВ; – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала АВ;
 , ,  – локальный привод (менее мощный, широкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки точного канала АВ; – локальный привод (менее мощный, широкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки точного канала АВ;
 , , 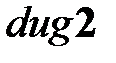 – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала ППУ; – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала ППУ;
 , , 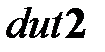 – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала ППУ; – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала ППУ;

Рис. 13.1
 – входное воздействие (координаты цели в абсолютной СК – обозначается верхним индексом «а»); – входное воздействие (координаты цели в абсолютной СК – обозначается верхним индексом «а»);
 – суммарная угловая поправка стрельбы; – суммарная угловая поправка стрельбы;
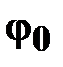 – угловое положение ЛА в абсолютной СК; – угловое положение ЛА в абсолютной СК;
 , ,  – выходные угловые координаты нагрузок грубого канала и суммы поворотов грубого и точного каналов двухканального СП АВ, соответственно; – выходные угловые координаты нагрузок грубого канала и суммы поворотов грубого и точного каналов двухканального СП АВ, соответственно;
 , ,  – выходные угловые координаты нагрузок грубого канала и суммы поворотов грубого и точного каналов двухканального СП ППУ, соответственно; – выходные угловые координаты нагрузок грубого канала и суммы поворотов грубого и точного каналов двухканального СП ППУ, соответственно;
 – алгоритмически сформированное входное воздействие на двухканальный СП ППУ; – алгоритмически сформированное входное воздействие на двухканальный СП ППУ;
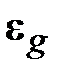 , , 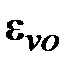 – ошибки отработки входного воздействия – ошибки отработки входного воздействия  локальным грубым СП и суммарным воздействием грубого и точного СП (собственно ошибка двухканального СП АВ); локальным грубым СП и суммарным воздействием грубого и точного СП (собственно ошибка двухканального СП АВ);
 и и  – ошибки отработки входного воздействия – ошибки отработки входного воздействия  локальным грубым СП и суммарным воздействием грубого и точного СП (собственно ошибка двухканального СП ППУ); локальным грубым СП и суммарным воздействием грубого и точного СП (собственно ошибка двухканального СП ППУ);
 – ошибка наведения на упрежденное положение цели последовательного объединения двухканальных СП. – ошибка наведения на упрежденное положение цели последовательного объединения двухканальных СП.
Каждый из 4-х представленных на рис. 13.1 приводов соответствует традиционной структурной схеме на основе скоростного двигателя постоянного тока (ДПТ), размещенного на подвижном основании, граф которого показан на рис. 12.3. Структура двухканального СП комбинированного управления соответствует рис. 12.13.
Учет динамики измерительных устройств на двухканальную СН
Примем структуру измерителя параметра 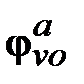 без формирования дополнительных связей, тогда граф, соответствующий структуре по рис. 13.3, принимает вид, как показано на рис. 13.4. без формирования дополнительных связей, тогда граф, соответствующий структуре по рис. 13.3, принимает вид, как показано на рис. 13.4.

Рис. 13.4
Появление в обратной связи двух СП датчиков угла, по измерениям которых и осуществляется замыкание может привести к изменению динамики замкнутого контура, но только при несоблюдении определенных условий.
Рассмотрим рис. 13.5, на котором показаны приближенные ЛАХ такого контура.
Верны следующие соотношения (исходя из ПФ замкнутого контура  и обязательного равенства на низких частотах и обязательного равенства на низких частотах  ): ):
 >>1 → >>1 →  ; ;  → плавный переход от → плавный переход от  к к  ; ;
 <<1 → <<1 →  . .

Рис. 13.5
Поэтому из ЛАХ по рис. 13.5 следует, что для снижения влияния 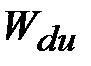 на динамику замкнутого контура необходимо обеспечить большую частоту пропускания датчика угла поворота по отношению к полосе пропускания разомкнутой части привода: на динамику замкнутого контура необходимо обеспечить большую частоту пропускания датчика угла поворота по отношению к полосе пропускания разомкнутой части привода:
 > >  . .
Сравнение динамической точности одноканальной и многоканальных СН комбинированного управления
Раздел 14 ОСОБЕННОСТИ АППАРАТУРНОЙ РЕАЛИЗАЦИИ БОРТОВОЙ СН – ОПТИЧЕСКИЙ ПЕЛЕНГАТОР
Гироскоп
Гироскопом (симметрическим гироскопом) называется твердое тело, вращающееся вокруг неподвижной точки  и обладающее осью и обладающее осью 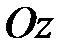 динамической симметрии (главная центральная ось инерции), которая проходит через центр инерции (масс) гироскопа (рис. 15.1 а). динамической симметрии (главная центральная ось инерции), которая проходит через центр инерции (масс) гироскопа (рис. 15.1 а).
Гироскоп называется уравновешенным, если точка  совпадает с центром масс (моменты всех внешних сил, включая и силу тяжести, относительно центра масс гироскопа равны нулю: совпадает с центром масс (моменты всех внешних сил, включая и силу тяжести, относительно центра масс гироскопа равны нулю: 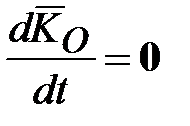 , где , где 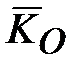 - кинетический момент, что следует из теоремы моментов относительно неподвижного центра: - кинетический момент, что следует из теоремы моментов относительно неподвижного центра: 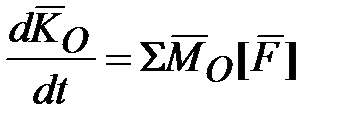 ). ).
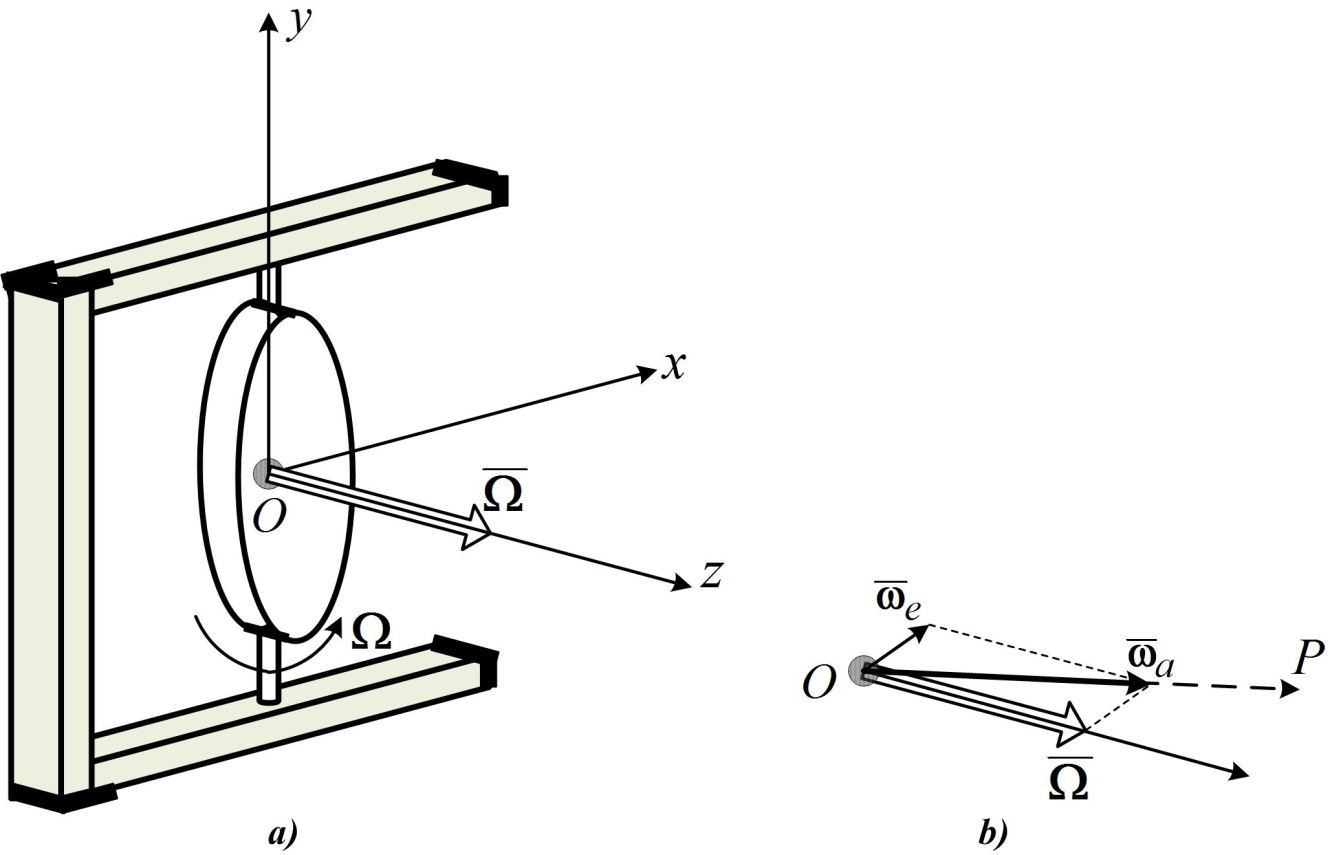
Рис. 15.1
В гироскопических приборах ротор гироскопа обычно закрепляют в кардановом подвесе, позволяющем ротору совершить любой поворот вокруг неподвижного центра подвеса, совпадающего с центром масс (ЦМ) ротора гироскопа (имеется три степени свободы).
Карданов подвес - универсальная шарнирная опора, позволяющая закреплённому в ней объекту вращаться одновременно в нескольких плоскостях. Основная идея карданова подвеса: несколько колец, расположенных одно внутри другого, соединяются в двух противоположных точках, что дает им возможность вращаться относительно друг друга. Если в центре колец поместить груз, то он будет сохранять вертикальное положение. Какие бы движения ни совершали кольца, груз останется неподвижной, поскольку кольца гасят колебания.
Если в кардановом подвесе закрепить вращающееся тело, то оно будет сохранять направление оси вращения независимо от ориентации самого подвеса. Карданов подвес обеспечивает вращающемуся телу свободный поворот в пространстве вокруг трех взаимно перпендикулярных осей, пересекающихся в одной точке, называемой точкой подвеса. Эта точка при любых указанных поворотах остается неподвижной (рис. 15.2).

Точка подвеса
Рис. 15.2
15.1.1 Элементарная (прецессионная) теория гироскопов ( >> >> 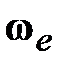 ) )
В общем случае кроме угловой скорости  вращения твердого массивного тела вокруг оси вращения твердого массивного тела вокруг оси 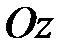 существует угловая скорость существует угловая скорость  поворота оси поворота оси 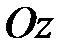 вокруг точки вокруг точки  (может иметь произвольное направление в пространстве), как показано на рис. 15.1 b. (может иметь произвольное направление в пространстве), как показано на рис. 15.1 b.
В каждый момент времени абсолютная угловая скорость гироскопа: 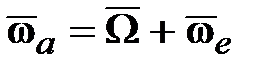 . Его суммарный поворот вокруг неподвижной точки . Его суммарный поворот вокруг неподвижной точки  слагается из серии элементарных поворотов с угловой скоростью слагается из серии элементарных поворотов с угловой скоростью 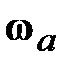 вокруг мгновенных осей вращения вокруг мгновенных осей вращения 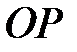 . При выполнении условия . При выполнении условия  >> >> 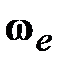 угол угол 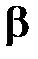 (рис. 15.1 b) очень мал и можно принять (рис. 15.1 b) очень мал и можно принять 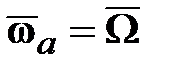 , а ось , а ось 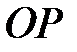 в любой момент времени будет совпадать с осью в любой момент времени будет совпадать с осью 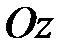 гироскопа. гироскопа.
В этом случае кинетический момент 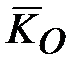 гироскопа относительно точки гироскопа относительно точки  можно также считать в любой момент времени направленным вдоль оси можно также считать в любой момент времени направленным вдоль оси 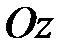 и численно равным и численно равным 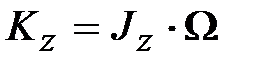 (основное допущение элементарной теории гироскопа). (основное допущение элементарной теории гироскопа).
В общем случае можно записать:
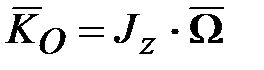 , ,
где полагаем, что ось  и вектор и вектор 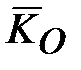 все время направлены вдоль одной и той же прямой; все время направлены вдоль одной и той же прямой;
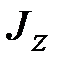 ‒ момент инерции гироскопа относительно оси ‒ момент инерции гироскопа относительно оси 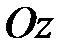 . .
Для уравновешенного гироскопа с точкой закрепления центра масс (свободный гироскоп), если пренебречь трением, можно записать 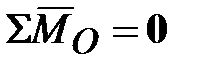 ( (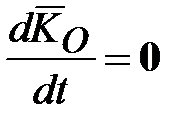 ) и ) и 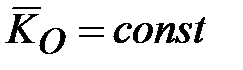 . Следовательно, ось свободного гироскопа сохраняет неизменное направление в пространстве по отношению к инерциальной (абсолютной) СК. . Следовательно, ось свободного гироскопа сохраняет неизменное направление в пространстве по отношению к инерциальной (абсолютной) СК.
Пусть на ось гироскопа через опору действует сила 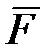 (рис. 15.3), момент которой относительно центра масс (рис. 15.3), момент которой относительно центра масс  равен равен 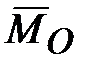 (или действует пара сил (или действует пара сил 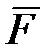 , , 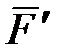 с моментом, равным с моментом, равным 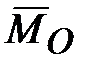 ). Тогда в соответствии с теоремой моментов (производная по времени от главного момента количества движения системы относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относительно того же центра ). Тогда в соответствии с теоремой моментов (производная по времени от главного момента количества движения системы относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относительно того же центра 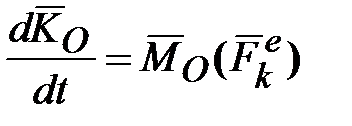 , где , где 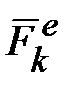 - равнодействующая всех внешних сил, действующих на данную систему): - равнодействующая всех внешних сил, действующих на данную систему):
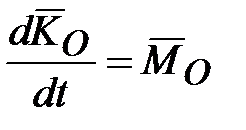 или или 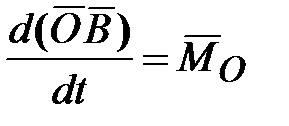 , ,
где:  - точка оси - точка оси 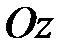 , совпадающая с концом вектора , совпадающая с концом вектора 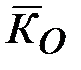 ; ;
- вектор 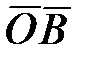 совпадает с вектором совпадает с вектором 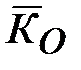 . .
Учитывая, что производная от вектора 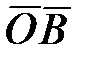 по времени равна скорости по времени равна скорости 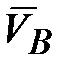 точки точки 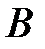 , получаем: , получаем:
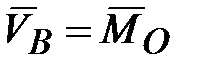 ( (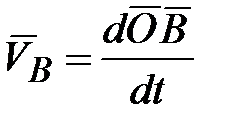 ). (15.1) ). (15.1)
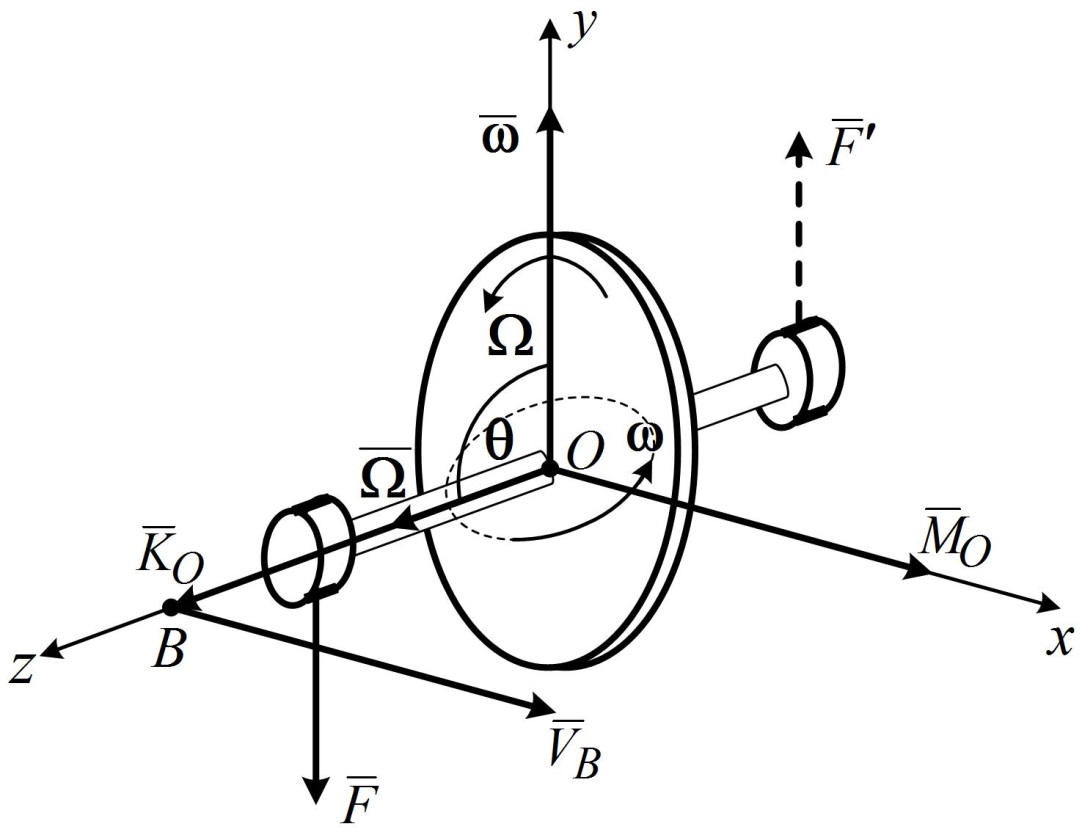
Рис. 15.3
Данное равенство соответствует теоремеРезаля: скорость конца вектора кинетического момента тела (гироскопа) относительно центра  равняется по модулю и по направлению главному моменту внешних сил относительно того же центра. равняется по модулю и по направлению главному моменту внешних сил относительно того же центра.
Следовательно, точка  , а с нею и главная ось гироскопа, будет перемещаться по направлению вектора , а с нею и главная ось гироскопа, будет перемещаться по направлению вектора  . Т.е., если на ось быстро вращающегося гироскопа подействует сила, то ось начнет отклоняться не в сторону действия силы, а по направлению, которое имеет вектор . Т.е., если на ось быстро вращающегося гироскопа подействует сила, то ось начнет отклоняться не в сторону действия силы, а по направлению, которое имеет вектор 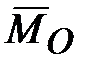 момента этой силы относительно неподвижной точки момента этой силы относительно неподвижной точки  гироскопа (перпендикулярно этой силе). гироскопа (перпендикулярно этой силе).
Из равенства (15.1) следует, что когда действие силы прекратится, то 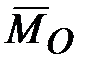 обращается в нуль и, следовательно, обращается в нуль и, следовательно, 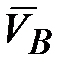 также обращается в нуль, и ось гироскопа останавливается. Таким образом, гироскоп не сохраняет движения, сообщенного ему силой. Если действие силы является кратковременным (толчок), то ось гироскопа практически не изменит своего направления (точнее ось начнет совершать вблизи начального положения высокочастотные колебания малой амплитуды - нутация, которые при наличии сопротивления затухнут, и ось придет в положение, близкое к своему начальному) - это проявление устойчивости оси быстро вращающегося гироскопа. также обращается в нуль, и ось гироскопа останавливается. Таким образом, гироскоп не сохраняет движения, сообщенного ему силой. Если действие силы является кратковременным (толчок), то ось гироскопа практически не изменит своего направления (точнее ось начнет совершать вблизи начального положения высокочастотные колебания малой амплитуды - нутация, которые при наличии сопротивления затухнут, и ось придет в положение, близкое к своему начальному) - это проявление устойчивости оси быстро вращающегося гироскопа.
Прецессия
Допустим, что сила 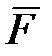 или пара сил или пара сил 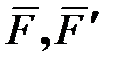 (рис. 15.3) действует на гироскоп во все время его работы, постоянно оставаясь в плоскости (рис. 15.3) действует на гироскоп во все время его работы, постоянно оставаясь в плоскости 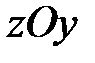 (к примеру, это могла бы быть сила тяжести). Выше мы отметили, что ось (к примеру, это могла бы быть сила тяжести). Выше мы отметили, что ось 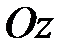 в сторону действия силы не отклоняется, поэтому угол в сторону действия силы не отклоняется, поэтому угол 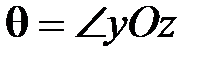 остаётся всё время постоянным, а скорость остаётся всё время постоянным, а скорость  - перпендикулярной плоскости - перпендикулярной плоскости 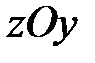 . Следовательно, ось гироскопа будет вращаться (прецессировать) вокруг оси . Следовательно, ось гироскопа будет вращаться (прецессировать) вокруг оси 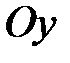 с некоторой угловой скорость с некоторой угловой скорость 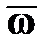 , называемой угловой скоростью прецессии. , называемой угловой скоростью прецессии.
Так как ось 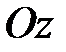 вращается вокруг оси вращается вокруг оси  с угловой скоростью с угловой скоростью 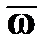 (рис. 15.3), то верна формула Эйлера (рис. 15.3), то верна формула Эйлера 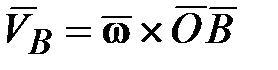 (вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки): (вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки):
 , ,
и из равенства (15.1) получается:
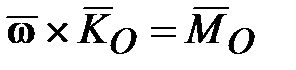 . (15.2) . (15.2)
Уравнение (15.2) является исходным приближенным уравнением элементарной (прецессионной) теории гироскопа (в элементарной теории гироскопа нутация не учитывается).
Из уравнения (15.2) следует:
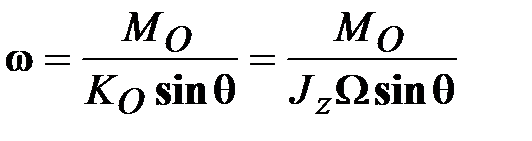 (15.3) (15.3)
Чем больше 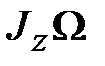 , тем меньше , тем меньше  и тем большую точность даёт элементарная теория гироскопа. и тем большую точность даёт элементарная теория гироскопа.
Гироскопический эффект
Пусть гироскоп имеет только две степени свободы: поворот вокруг оси 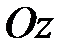 и, вместе с кольцом 2, - вокруг оси и, вместе с кольцом 2, - вокруг оси 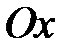 (двухстепенной гироскоп), как это показано на рис. 15.4. В этом случае, если толкнуть кольцо 2, то оно начнет свободно вращаться вокруг оси (двухстепенной гироскоп), как это показано на рис. 15.4. В этом случае, если толкнуть кольцо 2, то оно начнет свободно вращаться вокруг оси 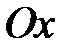 , в то время как трехстепенной гироскоп на такие толчки практически не реагирует. Не реагирует трехстепенной гироскоп и на вращение основания, сохраняя постоянным направление своей оси , в то время как трехстепенной гироскоп на такие толчки практически не реагирует. Не реагирует трехстепенной гироскоп и на вращение основания, сохраняя постоянным направление своей оси 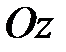 . .

Рис. 15.4
Пусть основание 1 вращается вокруг оси 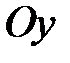 (или любой параллельной ей оси) с угловой скоростью (или любой параллельной ей оси) с угловой скоростью 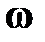 ( ( >> >> 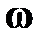 ). Вращаясь вместе с основанием, гироскоп совершает вынужденную прецессию вокруг оси ). Вращаясь вместе с основанием, гироскоп совершает вынужденную прецессию вокруг оси 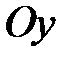 . Согласно уравнению (15.2) на ротор 3 гироскопа должен действовать момент . Согласно уравнению (15.2) на ротор 3 гироскопа должен действовать момент 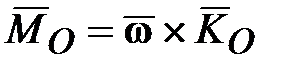 , который, очевидно, могут создать только силы , который, очевидно, могут создать только силы 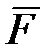 , , 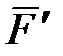 давления подшипников давления подшипников 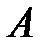 , , 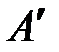 на ось ротора. Так как центр масс на ось ротора. Так как центр масс  ротора 3 гироскопа неподвижен, то по теореме о движении центра масс ( ротора 3 гироскопа неподвижен, то по теореме о движении центра масс (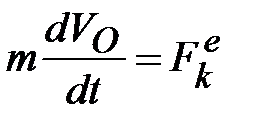 ) должно выполняться равенство ) должно выполняться равенство 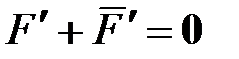 , и, следовательно, силы, , и, следовательно, силы, 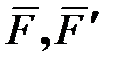 образуют пару, приложенную к ротору гироскопа. образуют пару, приложенную к ротору гироскопа.
Но, когда подшипники действуют на ось ротора с силами 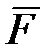 , , 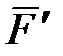 , то по третьему закону динамики (две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны) ось ротора гироскопа будет одновременно действовать на подшипники , то по третьему закону динамики (две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны) ось ротора гироскопа будет одновременно действовать на подшипники 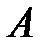 , , 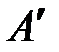 с такими же по модулю и противоположными по направлению силами с такими же по модулю и противоположными по направлению силами  и и 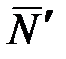 . .
Пара сил 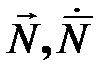 называется гироскопической парой, а её момент называется гироскопической парой, а её момент 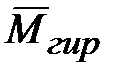 - моментом гироскопической пары или гироскопическим моментом (моментом гироскопической реакции). - моментом гироскопической пары или гироскопическим моментом (моментом гироскопической реакции).
Поскольку момент  противоположен моменту противоположен моменту 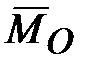 ( (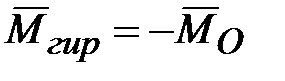 ), то: ), то:
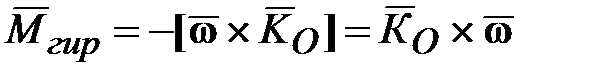 и и
 . (15.4) . (15.4)
Правило Н.Е. Жуковского: если быстро вращающемуся гироскопу сообщить вынужденное прецессионное движение, то на подшипники, в которых закреплена ось ротора гироскопа, начнет действовать гироскопическая пара с моментом  , стремящаяся кратчайшим путем установить ось ротора параллельно оси прецессии так, чтобы направления векторов , стремящаяся кратчайшим путем установить ось ротора параллельно оси прецессии так, чтобы направления векторов  и и 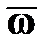 совпали. совпали.
Под действием гироскопической пары кольцо 2 начнет вращаться вместе с ротором вокруг оси 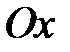 ; при этом угол ; при этом угол  , а с ним и момент , а с ним и момент 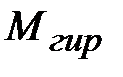 будут уменьшаться, и, когда будет выполнено равенство будут уменьшаться, и, когда будет выполнено равенство  , вращение кольца 2 прекратится. , вращение кольца 2 прекратится.
Правило прецессии
В силу общего закона динамики вращательного движения ( , т.е. изменение главного кинетического момента , т.е. изменение главного кинетического момента  определяется выражением определяется выражением  ) любой внешний момент, вектор которого не совпадает по направлению с вектором ) любой внешний момент, вектор которого не совпадает по направлению с вектором  , изменяет положение вектора главного кинетического момента гироскопа , изменяет положение вектора главного кинетического момента гироскопа  с угловой скоростью прецессии: с угловой скоростью прецессии:
 , ,
где:  - проекция вектора внешнего момента на экваториальную плоскость ротора гироскопа (плоскость, проходящая через точу - проекция вектора внешнего момента на экваториальную плоскость ротора гироскопа (плоскость, проходящая через точу  и перпендикулярная вектору и перпендикулярная вектору  ), равная ), равная 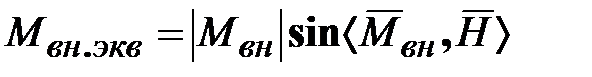 . .
Как было показано выше, движение с угловой скоростью прецессии происходит таким образом, чтобы совместить вектор  с вектором с вектором  по кратчайшему пути. по кратчайшему пути.
15.1.4.2 Правило гироскопической реакции
При действии на гироскоп, обладающий кинетическим моментом  , переносной угловой скорости , переносной угловой скорости  возникает момент гироскопической реакции: возникает момент гироскопической реакции:
 , ,
где:  , ,
а вектор момента гироскопической пары направлен так, что  совмещает по кратчайшему пути вектор совмещает по кратчайшему пути вектор  (вектор (вектор  совпадает по направлению с вектором совпадает по направлению с вектором  ) с вектором ) с вектором  : :
 . .
Направление гироскопических сил можно ищется с помощью правила Н.Е. Жуковского: гироскопический момент реакции стремится совместить вектор  гироскопа с направлением переносной угловой скорости гироскопа с направлением переносной угловой скорости  по кратчайшему пути. по кратчайшему пути.
Следовательно, можно сформулировать следующий вывод.
При действии на гироскоп с кинетическим моментом  внешнего момента внешнего момента  , вектор которого не совпадает по направлению с вектором , вектор которого не совпадает по направлению с вектором 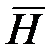 , возникают два гироскопических момента: , возникают два гироскопических момента:
первый – вызывает вынужденную прецессию (при наличии необходимой степени свободы) с угловой скоростью:  в направлении совмещения по кратчайшему пути вектора в направлении совмещения по кратчайшему пути вектора  с вектором с вектором  ; ;
второй - уравновешивает внешний момент  . .
15.1.4 Порядок формирования гироскопических моментов
Последовательность формирования этих гироскопических моментов демонстрируется на рис. 15.6, где приняты следующие обозначения:

Рис. 15.6
- СК 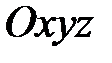 соответствует исходному (нулевому) положению осей карданова подвеса; соответствует исходному (нулевому) положению осей карданова подвеса;
- СК  соответствует текущему положению осей карданова подвеса; соответствует текущему положению осей карданова подвеса;
-  - угол поворота вокруг оси - - угол поворота вокруг оси - 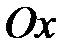 ; ;
-  - угол поворота вокруг оси - - угол поворота вокруг оси - 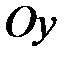 ; ;
-  - момент гироскопический реакции, направленный вдоль оси - момент гироскопический реакции, направленный вдоль оси  , возникающий при действии на гироскоп переносной угловой скорости , возникающий при действии на гироскоп переносной угловой скорости  (вызывает перемещение с угловой скоростью вынужденной прецессии (вызывает перемещение с угловой скоростью вынужденной прецессии 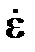 ); );
-  - момент гироскопический реакции вдоль оси - момент гироскопический реакции вдоль оси  при действии на гироскоп вынужденной прецессии с угловой скоростью при действии на гироскоп вынужденной прецессии с угловой скоростью  ; ;
-  - момент инерции подвижных частей (полезная нагрузка при использовании гироскопа в качестве гироскопического привода) относительно оси - момент инерции подвижных частей (полезная нагрузка при использовании гироскопа в качестве гироскопического привода) относительно оси  ; ;
-  - момент инерции подвижных частей (полезная нагрузка) относительно оси - момент инерции подвижных частей (полезная нагрузка) относительно оси  ; ;
-  - инерционный момент, характеризующий динамику разгона при повороте вокруг оси - инерционный момент, характеризующий динамику разгона при повороте вокруг оси  ; ;
-  - инерционный момент, характеризующий динамику разгона при повороте вокруг оси - инерционный момент, характеризующий динамику разгона при повороте вокруг оси  ; ;
-  - внешний (возмущающий или управляющий) моменты. - внешний (возмущающий или управляющий) моменты.
Действие внешнего момента  вдоль оси вдоль оси  (в экваториальной плоскости (в экваториальной плоскости  ) по второму закону Ньютона вызывает появление угловой скорости ) по второму закону Ньютона вызывает появление угловой скорости  нагрузки с моментом инерции нагрузки с моментом инерции  , являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент , являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент  (лежит в экваториальной плоскости, но ортогонален по отношению к моменту, его вызвавшему), направленный таким образом, чтобы по кратчайшему пути совместить вектор (лежит в экваториальной плоскости, но ортогонален по отношению к моменту, его вызвавшему), направленный таким образом, чтобы по кратчайшему пути совместить вектор  с вектором с вектором  . .
Действие внешнего момента  вдоль оси вдоль оси  по второму закону Ньютона вызывает появление угловой скорости по второму закону Ньютона вызывает появление угловой скорости  нагрузки с моментом инерции нагрузки с моментом инерции  , являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент , являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент  , направленный таким образом, чтобы по кратчайшему пути совместить вектор , направленный таким образом, чтобы по кратчайшему пути совместить вектор 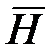 с вектором с вектором  . Гироскопический момент . Гироскопический момент  уравновешивает внешний момент уравновешивает внешний момент 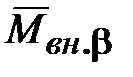 , и движение останавливается. , и движение останавливается.
Причинно-следственная последовательность физических явлений по рис. 15.6 выглядит следующим образом:
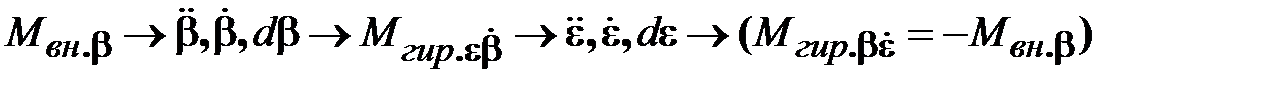 . .
Даже очень небольшой момент управления  , создаваемый моментным двигателем , создаваемый моментным двигателем  , вызывает появление значительного движущего момента относительно ортогональной оси, превышающего управляющий момент на несколько порядков. Таким образом, гироскоп может выполнять функции усилителя момента и использоваться в качестве силового гиропривода. , вызывает появление значительного движущего момента относительно ортогональной оси, превышающего управляющий момент на несколько порядков. Таким образом, гироскоп может выполнять функции усилителя момента и использоваться в качестве силового гиропривода.
15.1.5 Акселерометр
Акселерометр (датчик линейного ускорения подвижного объекта) является механическим прибором с одной степенью свободы, содержащим чувствительную массу, перемещение которой под действием сил инерции относительно корпуса прибора ограничено упругой связью и несёт информацию об ускорении.
На рис. 15.8 показана простейшая схема осевого акселерометра.

Рис. 15.8
Корпус 1 акселерометра связан с подвижным объектом 2 через упругий подвес 3. Ось Х, вдоль которой перемещается под действием сил инерции груз 2, является осью чувствительности. Перемещение х груза 2 вдоль оси Х измеряется с помощью датчика 4 линейных перемещений; демпфирование собственных колебаний груза 2 осуществляется демпфером 5.
Если акселерометр установить на ЛА, вектор линейного ускорения  которого расположен под углом которого расположен под углом  к горизонту, то схема сил, действующих на акселерометр, показана на рис. 15.9. к горизонту, то схема сил, действующих на акселерометр, показана на рис. 15.9.

Рис. 15.9
К чувствительному элементу акселерометра (груз 2) приложены следующие силы (после окончания переходных процессов):
‒ сила инерции  (она прикладывается к элементу связи груза 2, характеризуемого упругостью (она прикладывается к элементу связи груза 2, характеризуемого упругостью  ); );
‒ упругая сила  деформации пружины; деформации пружины;
‒ составляющая силы тяжести  вдоль оси чувствительности акселерометра. вдоль оси чувствительности акселерометра.
С учетом направлений векторов сил можно записать следующее скалярное уравнение баланса сил для установившегося режима:
 , ,
откуда следует, что перемещение  массы 2 равно: массы 2 равно:
 . (15.6) . (15.6)
Величина  называется «кажущимся» ускорением, статический коэффициент перед которым является характеристикой чувствительности акселерометра. называется «кажущимся» ускорением, статический коэффициент перед которым является характеристикой чувствительности акселерометра.
В дальнейшем будем обозначать  и и  . .
В переходных режимах на тело 2 дополнительно действует демпфирующая сила 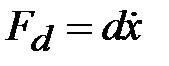 вдоль оси чувствительности акселерометра. вдоль оси чувствительности акселерометра.
Движение груза 2 состоит из переносного движения вместе с корпусом 1 и из относительного движения по отношению к этому корпусу (второй закон Ньютона без учета трения):
В результате можно записать ( ): ):

где:  - проекция переносного ускорения на ось Х чувствительности, равного абсолютному ускорению той точки корпуса 1 акселерометра, с которой в данный момент времени совпадает центр масс груза 2 (при малых размерах акселерометра переносное ускорение - проекция переносного ускорения на ось Х чувствительности, равного абсолютному ускорению той точки корпуса 1 акселерометра, с которой в данный момент времени совпадает центр масс груза 2 (при малых размерах акселерометра переносное ускорение  можно принять равным абсолютному ускорению центральной точки корпуса 1 акселерометра); можно принять равным абсолютному ускорению центральной точки корпуса 1 акселерометра);
 - относительное ускорение, равное ускорению центра масс груза 2 относительно корпуса 4 акселерометра. - относительное ускорение, равное ускорению центра масс груза 2 относительно корпуса 4 акселерометра.
Последнее выражение можно записать в виде:
 . (15.7) . (15.7)
При  получается уравнение относительно равновесия для груза 2: получается уравнение относительно равновесия для груза 2:
 . .
Следовательно, акселерометр измеряет величину  . .
Для объекта, который находится в покое или движется прямолинейно и равномерно ( ) можно записать следующее соотношение: ) можно записать следующее соотношение:
 , ,
которое является основой для построения акселерометрических датчиков абсолютного угла.
Типы гироскопов
Раздел 13 ДИНАМИЧЕСКАЯ ТОЧНОСТЬ МНОГОКАНАЛЬНОЙ КОМБИНИРОВАННОЙ СН
13.1 Функциональная схема двухканальной комбинированной СН при идеальном (пеленгатор) и разделенном (пушечная установка) суммировании угловых координат
Будем рассматривать следующий вариант построения структуры объединения СП (структуры СН):
‒ СП АВ представляет собой двухканальный привод комбинированного управления с идеальным суммирование выходных угловых координат локальных приводов;
‒ СП ППУ представляет собой двухканальный привод комбинированного управления с суммирование выходных угловых координат локальных приводов по принципу разделенной нагрузки.
В соответствии с материалами разделов 7, 9, 10 и 12 будем рассматривать СН, в которой каждый из следящих систем АВ и ППУ представляет собой двухканальный СП. В этом случае функциональную схему оптико-механической части многоканальной СН можно представить, как это показано на рис. 13.1, где приняты следующие обозначения:
 – пеленгационное устройство грубого канала АВ (широкое поле зрения); – пеленгационное устройство грубого канала АВ (широкое поле зрения);
 – пеленгационное устройство совокупности грубого и точного каналов АВ (узкое поле зрения); – пеленгационное устройство совокупности грубого и точного каналов АВ (узкое поле зрения);
 , ,  – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала АВ; – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала АВ;
 , ,  – локальный привод (менее мощный, широкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки точного канала АВ; – локальный привод (менее мощный, широкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки точного канала АВ;
 , , 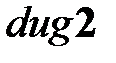 – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала ППУ; – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала ППУ;
 , , 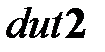 – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала ППУ; – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала ППУ;

Рис. 13.1
 – входное воздействие (координаты цели в абсолютной СК – обозначается верхним индексом «а»); – входное воздействие (координаты цели в абсолютной СК – обозначается верхним индексом «а»);
 – суммарная угловая поправка стрельбы; – суммарная угловая поправка стрельбы;
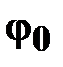 – угловое положение ЛА в абсолютной СК; – угловое положение ЛА в абсолютной СК;
 , ,  – выходные угловые координаты нагрузок грубого канала и суммы поворотов грубого и точного каналов двухканального СП АВ, соответственно; – выходные угловые координаты нагрузок грубого канала и суммы поворотов грубого и точного каналов двухканального СП АВ, соответственно;
 , ,  – выходные угловые координаты нагрузок грубого канала и суммы поворотов грубого и точного каналов двухканального СП ППУ, соответственно; – выходные угловые координаты нагрузок грубого канала и суммы поворотов грубого и точного каналов двухканального СП ППУ, соответственно;
 – алгоритмически сформированное входное воздействие на двухканальный СП ППУ; – алгоритмически сформированное входное воздействие на двухканальный СП ППУ;

| 


 – пеленгационное устройство грубого канала АВ (широкое поле зрения);
– пеленгационное устройство грубого канала АВ (широкое поле зрения); – пеленгационное устройство совокупности грубого и точного каналов АВ (узкое поле зрения);
– пеленгационное устройство совокупности грубого и точного каналов АВ (узкое поле зрения); ,
,  – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала АВ;
– локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала АВ; ,
,  – локальный привод (менее мощный, широкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки точного канала АВ;
– локальный привод (менее мощный, широкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки точного канала АВ; ,
, 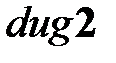 – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала ППУ;
– локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала ППУ; ,
, 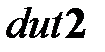 – локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала ППУ;
– локальный привод (более мощный, узкополосный) и датчик угла поворота в абсолютной СК функциональной нагрузки грубого канала ППУ;
 – входное воздействие (координаты цели в абсолютной СК – обозначается верхним индексом «а»);
– входное воздействие (координаты цели в абсолютной СК – обозначается верхним индексом «а»); – суммарная угловая поправка стрельбы;
– суммарная угловая поправка стрельбы;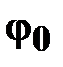 – угловое положение ЛА в абсолютной СК;
– угловое положение ЛА в абсолютной СК; ,
,  – выходные угловые координаты нагрузок грубого канала и суммы поворотов грубого и точного каналов двухканального СП АВ, соответственно;
– выходные угловые координаты нагрузок грубого канала и суммы поворотов грубого и точного каналов двухканального СП АВ, соответственно; ,
,  – выходные угловые координаты нагрузок грубого канала и суммы поворотов грубого и точного каналов двухканального СП ППУ, соответственно;
– выходные угловые координаты нагрузок грубого канала и суммы поворотов грубого и точного каналов двухканального СП ППУ, соответственно; – алгоритмически сформированное входное воздействие на двухканальный СП ППУ;
– алгоритмически сформированное входное воздействие на двухканальный СП ППУ;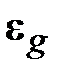 ,
, 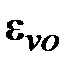 – ошибки отработки входного воздействия
– ошибки отработки входного воздействия  и
и  – ошибки отработки входного воздействия
– ошибки отработки входного воздействия  – ошибка наведения на упрежденное положение цели последовательного объединения двухканальных СП.
– ошибка наведения на упрежденное положение цели последовательного объединения двухканальных СП.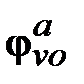 без формирования дополнительных связей, тогда граф, соответствующий структуре по рис. 13.3, принимает вид, как показано на рис. 13.4.
без формирования дополнительных связей, тогда граф, соответствующий структуре по рис. 13.3, принимает вид, как показано на рис. 13.4.
 и обязательного равенства на низких частотах
и обязательного равенства на низких частотах  ):
): >>1 →
>>1 →  ;
;  → плавный переход от
→ плавный переход от  к
к  ;
; .
.
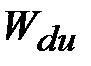 на динамику замкнутого контура необходимо обеспечить большую частоту пропускания датчика угла поворота по отношению к полосе пропускания разомкнутой части привода:
на динамику замкнутого контура необходимо обеспечить большую частоту пропускания датчика угла поворота по отношению к полосе пропускания разомкнутой части привода: >
>  .
. и обладающее осью
и обладающее осью 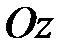 динамической симметрии (главная центральная ось инерции), которая проходит через центр инерции (масс) гироскопа (рис. 15.1 а).
динамической симметрии (главная центральная ось инерции), которая проходит через центр инерции (масс) гироскопа (рис. 15.1 а).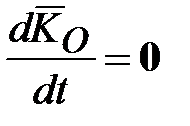 , где
, где 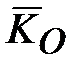 - кинетический момент, что следует из теоремы моментов относительно неподвижного центра:
- кинетический момент, что следует из теоремы моментов относительно неподвижного центра: 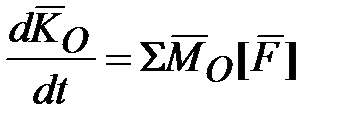 ).
).

 >>
>> 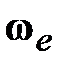 )
) вращения твердого массивного тела вокруг оси
вращения твердого массивного тела вокруг оси  поворота оси
поворота оси 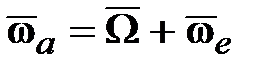 . Его суммарный поворот вокруг неподвижной точки
. Его суммарный поворот вокруг неподвижной точки  вокруг мгновенных осей вращения
вокруг мгновенных осей вращения  . При выполнении условия
. При выполнении условия  >>
>> 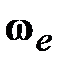 угол
угол 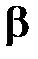 (рис. 15.1 b) очень мал и можно принять
(рис. 15.1 b) очень мал и можно принять 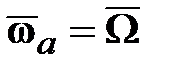 , а ось
, а ось 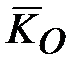 гироскопа относительно точки
гироскопа относительно точки 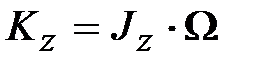 (основное допущение элементарной теории гироскопа).
(основное допущение элементарной теории гироскопа).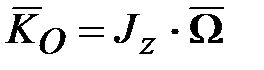 ,
, все время направлены вдоль одной и той же прямой;
все время направлены вдоль одной и той же прямой; ‒ момент инерции гироскопа относительно оси
‒ момент инерции гироскопа относительно оси 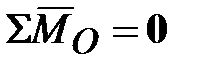 (
(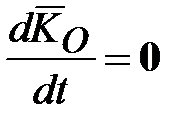 ) и
) и 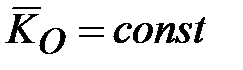 . Следовательно, ось свободного гироскопа сохраняет неизменное направление в пространстве по отношению к инерциальной (абсолютной) СК.
. Следовательно, ось свободного гироскопа сохраняет неизменное направление в пространстве по отношению к инерциальной (абсолютной) СК.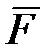 (рис. 15.3), момент которой относительно центра масс
(рис. 15.3), момент которой относительно центра масс 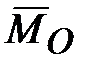 (или действует пара сил
(или действует пара сил 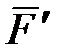 с моментом, равным
с моментом, равным 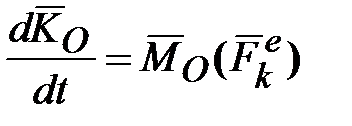 , где
, где 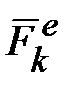 - равнодействующая всех внешних сил, действующих на данную систему):
- равнодействующая всех внешних сил, действующих на данную систему):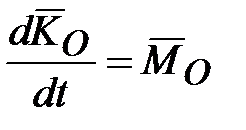 или
или 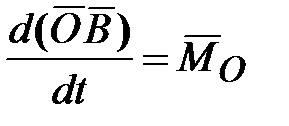 ,
, - точка оси
- точка оси 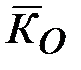 ;
;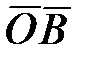 совпадает с вектором
совпадает с вектором 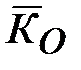 .
.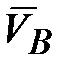 точки
точки  , получаем:
, получаем: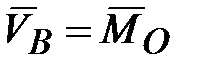 (
(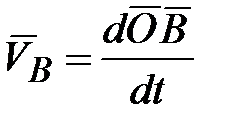 ). (15.1)
). (15.1)
 равняется по модулю и по направлению главному моменту внешних сил относительно того же центра.
равняется по модулю и по направлению главному моменту внешних сил относительно того же центра.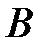 , а с нею и главная ось гироскопа, будет перемещаться по направлению вектора
, а с нею и главная ось гироскопа, будет перемещаться по направлению вектора 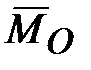 . Т.е., если на ось быстро вращающегося гироскопа подействует сила, то ось начнет отклоняться не в сторону действия силы, а по направлению, которое имеет вектор
. Т.е., если на ось быстро вращающегося гироскопа подействует сила, то ось начнет отклоняться не в сторону действия силы, а по направлению, которое имеет вектор 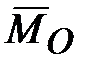 момента этой силы относительно неподвижной точки
момента этой силы относительно неподвижной точки  гироскопа (перпендикулярно этой силе).
гироскопа (перпендикулярно этой силе).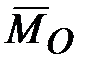 обращается в нуль и, следовательно,
обращается в нуль и, следовательно, 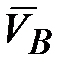 также обращается в нуль, и ось гироскопа останавливается. Таким образом, гироскоп не сохраняет движения, сообщенного ему силой. Если действие силы является кратковременным (толчок), то ось гироскопа практически не изменит своего направления (точнее ось начнет совершать вблизи начального положения высокочастотные колебания малой амплитуды - нутация, которые при наличии сопротивления затухнут, и ось придет в положение, близкое к своему начальному) - это проявление устойчивости оси быстро вращающегося гироскопа.
также обращается в нуль, и ось гироскопа останавливается. Таким образом, гироскоп не сохраняет движения, сообщенного ему силой. Если действие силы является кратковременным (толчок), то ось гироскопа практически не изменит своего направления (точнее ось начнет совершать вблизи начального положения высокочастотные колебания малой амплитуды - нутация, которые при наличии сопротивления затухнут, и ось придет в положение, близкое к своему начальному) - это проявление устойчивости оси быстро вращающегося гироскопа.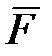 или пара сил
или пара сил 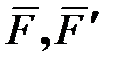 (рис. 15.3) действует на гироскоп во все время его работы, постоянно оставаясь в плоскости
(рис. 15.3) действует на гироскоп во все время его работы, постоянно оставаясь в плоскости 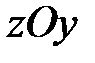 (к примеру, это могла бы быть сила тяжести). Выше мы отметили, что ось
(к примеру, это могла бы быть сила тяжести). Выше мы отметили, что ось 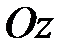 в сторону действия силы не отклоняется, поэтому угол
в сторону действия силы не отклоняется, поэтому угол 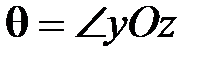 остаётся всё время постоянным, а скорость
остаётся всё время постоянным, а скорость  - перпендикулярной плоскости
- перпендикулярной плоскости 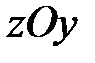 . Следовательно, ось гироскопа будет вращаться (прецессировать) вокруг оси
. Следовательно, ось гироскопа будет вращаться (прецессировать) вокруг оси 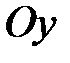 с некоторой угловой скорость
с некоторой угловой скорость 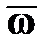 , называемой угловой скоростью прецессии.
, называемой угловой скоростью прецессии.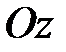 вращается вокруг оси
вращается вокруг оси  с угловой скоростью
с угловой скоростью 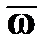 (рис. 15.3), то верна формула Эйлера
(рис. 15.3), то верна формула Эйлера 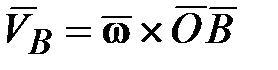 (вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки):
(вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки): ,
,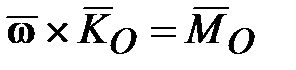 . (15.2)
. (15.2)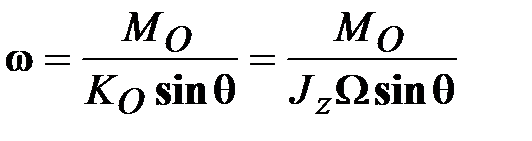 (15.3)
(15.3)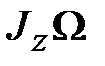 , тем меньше
, тем меньше  и тем большую точность даёт элементарная теория гироскопа.
и тем большую точность даёт элементарная теория гироскопа.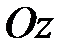 и, вместе с кольцом 2, - вокруг оси
и, вместе с кольцом 2, - вокруг оси 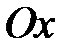 (двухстепенной гироскоп), как это показано на рис. 15.4. В этом случае, если толкнуть кольцо 2, то оно начнет свободно вращаться вокруг оси
(двухстепенной гироскоп), как это показано на рис. 15.4. В этом случае, если толкнуть кольцо 2, то оно начнет свободно вращаться вокруг оси 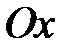 , в то время как трехстепенной гироскоп на такие толчки практически не реагирует. Не реагирует трехстепенной гироскоп и на вращение основания, сохраняя постоянным направление своей оси
, в то время как трехстепенной гироскоп на такие толчки практически не реагирует. Не реагирует трехстепенной гироскоп и на вращение основания, сохраняя постоянным направление своей оси 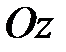 .
.
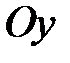 (или любой параллельной ей оси) с угловой скоростью
(или любой параллельной ей оси) с угловой скоростью 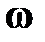 (
( >>
>> 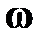 ). Вращаясь вместе с основанием, гироскоп совершает вынужденную прецессию вокруг оси
). Вращаясь вместе с основанием, гироскоп совершает вынужденную прецессию вокруг оси 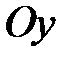 . Согласно уравнению (15.2) на ротор 3 гироскопа должен действовать момент
. Согласно уравнению (15.2) на ротор 3 гироскопа должен действовать момент 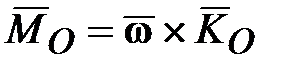 , который, очевидно, могут создать только силы
, который, очевидно, могут создать только силы 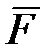 ,
, 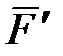 давления подшипников
давления подшипников 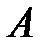 ,
, 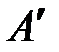 на ось ротора. Так как центр масс
на ось ротора. Так как центр масс  ротора 3 гироскопа неподвижен, то по теореме о движении центра масс (
ротора 3 гироскопа неподвижен, то по теореме о движении центра масс (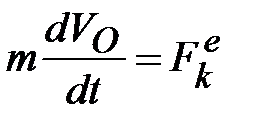 ) должно выполняться равенство
) должно выполняться равенство 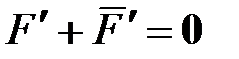 , и, следовательно, силы,
, и, следовательно, силы,  и
и 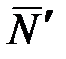 .
.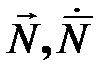 называется гироскопической парой, а её момент
называется гироскопической парой, а её момент 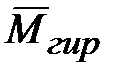 - моментом гироскопической пары или гироскопическим моментом (моментом гироскопической реакции).
- моментом гироскопической пары или гироскопическим моментом (моментом гироскопической реакции). противоположен моменту
противоположен моменту 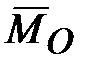 (
(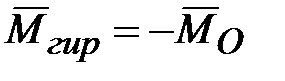 ), то:
), то: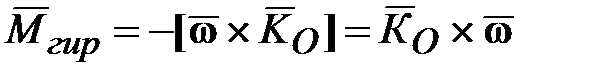 и
и . (15.4)
. (15.4) и
и  совпали.
совпали. ; при этом угол
; при этом угол  , а с ним и момент
, а с ним и момент 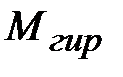 будут уменьшаться, и, когда будет выполнено равенство
будут уменьшаться, и, когда будет выполнено равенство 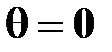 , вращение кольца 2 прекратится.
, вращение кольца 2 прекратится. , т.е. изменение главного кинетического момента
, т.е. изменение главного кинетического момента  определяется выражением
определяется выражением  ) любой внешний момент, вектор которого не совпадает по направлению с вектором
) любой внешний момент, вектор которого не совпадает по направлению с вектором  , изменяет положение вектора главного кинетического момента гироскопа
, изменяет положение вектора главного кинетического момента гироскопа  ,
, - проекция вектора внешнего момента на экваториальную плоскость ротора гироскопа (плоскость, проходящая через точу
- проекция вектора внешнего момента на экваториальную плоскость ротора гироскопа (плоскость, проходящая через точу 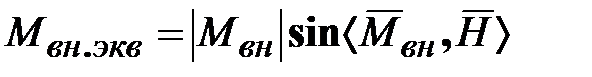 .
. по кратчайшему пути.
по кратчайшему пути. возникает момент гироскопической реакции:
возникает момент гироскопической реакции: ,
, ,
, совмещает по кратчайшему пути вектор
совмещает по кратчайшему пути вектор  ) с вектором
) с вектором  :
: .
. , вектор которого не совпадает по направлению с вектором
, вектор которого не совпадает по направлению с вектором 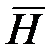 , возникают два гироскопических момента:
, возникают два гироскопических момента: в направлении совмещения по кратчайшему пути вектора
в направлении совмещения по кратчайшему пути вектора  с вектором
с вектором  ;
; .
.
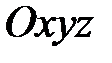 соответствует исходному (нулевому) положению осей карданова подвеса;
соответствует исходному (нулевому) положению осей карданова подвеса; соответствует текущему положению осей карданова подвеса;
соответствует текущему положению осей карданова подвеса; - угол поворота вокруг оси -
- угол поворота вокруг оси - 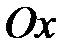 ;
; - угол поворота вокруг оси -
- угол поворота вокруг оси - 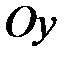 ;
; - момент гироскопический реакции, направленный вдоль оси
- момент гироскопический реакции, направленный вдоль оси  , возникающий при действии на гироскоп переносной угловой скорости
, возникающий при действии на гироскоп переносной угловой скорости  (вызывает перемещение с угловой скоростью вынужденной прецессии
(вызывает перемещение с угловой скоростью вынужденной прецессии 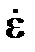 );
); - момент гироскопический реакции вдоль оси
- момент гироскопический реакции вдоль оси  при действии на гироскоп вынужденной прецессии с угловой скоростью
при действии на гироскоп вынужденной прецессии с угловой скоростью  ;
; - момент инерции подвижных частей (полезная нагрузка при использовании гироскопа в качестве гироскопического привода) относительно оси
- момент инерции подвижных частей (полезная нагрузка при использовании гироскопа в качестве гироскопического привода) относительно оси  ;
; - момент инерции подвижных частей (полезная нагрузка) относительно оси
- момент инерции подвижных частей (полезная нагрузка) относительно оси  ;
; - инерционный момент, характеризующий динамику разгона при повороте вокруг оси
- инерционный момент, характеризующий динамику разгона при повороте вокруг оси  ;
; - инерционный момент, характеризующий динамику разгона при повороте вокруг оси
- инерционный момент, характеризующий динамику разгона при повороте вокруг оси  ;
; - внешний (возмущающий или управляющий) моменты.
- внешний (возмущающий или управляющий) моменты. вдоль оси
вдоль оси  (в экваториальной плоскости
(в экваториальной плоскости  ) по второму закону Ньютона вызывает появление угловой скорости
) по второму закону Ньютона вызывает появление угловой скорости  нагрузки с моментом инерции
нагрузки с моментом инерции  , являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент
, являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент  (лежит в экваториальной плоскости, но ортогонален по отношению к моменту, его вызвавшему), направленный таким образом, чтобы по кратчайшему пути совместить вектор
(лежит в экваториальной плоскости, но ортогонален по отношению к моменту, его вызвавшему), направленный таким образом, чтобы по кратчайшему пути совместить вектор  .
. вдоль оси
вдоль оси  по второму закону Ньютона вызывает появление угловой скорости
по второму закону Ньютона вызывает появление угловой скорости  нагрузки с моментом инерции
нагрузки с моментом инерции  , являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент
, являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент  , направленный таким образом, чтобы по кратчайшему пути совместить вектор
, направленный таким образом, чтобы по кратчайшему пути совместить вектор 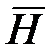 с вектором
с вектором  . Гироскопический момент
. Гироскопический момент  уравновешивает внешний момент
уравновешивает внешний момент 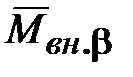 , и движение останавливается.
, и движение останавливается.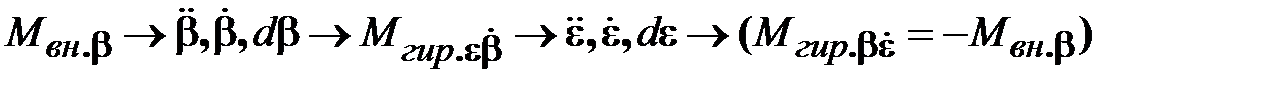 .
. , создаваемый моментным двигателем
, создаваемый моментным двигателем  , вызывает появление значительного движущего момента относительно ортогональной оси, превышающего управляющий момент на несколько порядков. Таким образом, гироскоп может выполнять функции усилителя момента и использоваться в качестве силового гиропривода.
, вызывает появление значительного движущего момента относительно ортогональной оси, превышающего управляющий момент на несколько порядков. Таким образом, гироскоп может выполнять функции усилителя момента и использоваться в качестве силового гиропривода.
 которого расположен под углом
которого расположен под углом  к горизонту, то схема сил, действующих на акселерометр, показана на рис. 15.9.
к горизонту, то схема сил, действующих на акселерометр, показана на рис. 15.9.
 (она прикладывается к элементу связи груза 2, характеризуемого упругостью
(она прикладывается к элементу связи груза 2, характеризуемого упругостью  );
); деформации пружины;
деформации пружины; вдоль оси чувствительности акселерометра.
вдоль оси чувствительности акселерометра. ,
, массы 2 равно:
массы 2 равно: . (15.6)
. (15.6) называется «кажущимся» ускорением, статический коэффициент перед которым является характеристикой чувствительности акселерометра.
называется «кажущимся» ускорением, статический коэффициент перед которым является характеристикой чувствительности акселерометра. и
и  .
.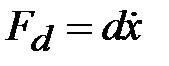 вдоль оси чувствительности акселерометра.
вдоль оси чувствительности акселерометра. ):
):
 - проекция переносного ускорения на ось Х чувствительности, равного абсолютному ускорению той точки корпуса 1 акселерометра, с которой в данный момент времени совпадает центр масс груза 2 (при малых размерах акселерометра переносное ускорение
- проекция переносного ускорения на ось Х чувствительности, равного абсолютному ускорению той точки корпуса 1 акселерометра, с которой в данный момент времени совпадает центр масс груза 2 (при малых размерах акселерометра переносное ускорение  можно принять равным абсолютному ускорению центральной точки корпуса 1 акселерометра);
можно принять равным абсолютному ускорению центральной точки корпуса 1 акселерометра); - относительное ускорение, равное ускорению центра масс груза 2 относительно корпуса 4 акселерометра.
- относительное ускорение, равное ускорению центра масс груза 2 относительно корпуса 4 акселерометра. . (15.7)
. (15.7) получается уравнение относительно равновесия для груза 2:
получается уравнение относительно равновесия для груза 2: .
. .
. ) можно записать следующее соотношение:
) можно записать следующее соотношение: ,
,


