
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение угловой скорости прецессии и момента инерции гироскопаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Лабораторная работа № 1.8.
Цель работы: ознакомление с гироскопом, проверка гироскопического эффекта, исследование прецессии гироскопа, определение угловой скорости прецессии и момента инерции гироскопа. Принадлежности: установка для изучения гироскопических эффектов. Описание гироскопа
Гироскоп представляет собой массивное симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии. Эту ось называют осью гироскопа.
              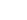                  Рассмотрим гироскоп с одной неподвижной точкой О на его оси. (рис.8.1). Точку 0 называют точкой опоры, или центром подвеса гироскопа. Если центр подвеса гироскопа совпадает с его центром масс, то результирующий момент сил тяжести всех частей гироскопа Рассмотрим гироскоп с одной неподвижной точкой О на его оси. (рис.8.1). Точку 0 называют точкой опоры, или центром подвеса гироскопа. Если центр подвеса гироскопа совпадает с его центром масс, то результирующий момент сил тяжести всех частей гироскопа 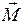 относительно 0 равен нулю. Такой гироскоп называется уравновешенным. После приведения уравновешенного гироскопа в быстрое вращение его ось будет сохранять свое направление в пространстве и сопротивляться всяким попыткам изменить это направление. Смещая груз m в ту или иную сторону от положения равновесия, вызываем разбаланс системы, в результате чего возникает вращающий момент относительно 0 равен нулю. Такой гироскоп называется уравновешенным. После приведения уравновешенного гироскопа в быстрое вращение его ось будет сохранять свое направление в пространстве и сопротивляться всяким попыткам изменить это направление. Смещая груз m в ту или иную сторону от положения равновесия, вызываем разбаланс системы, в результате чего возникает вращающий момент  , обусловленный действием силы тяжести mg груза. Величина вращающего момента , обусловленный действием силы тяжести mg груза. Величина вращающего момента 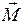 будет равна будет равна
где m – масса уравновешивающего груза; системы маховик – груз; Направление момента В случае вращающегося гироскопа его момент импульса
совпадающее по направленное с вектором
где поворот оси гироскопа
Если учесть, что
Из выражения для
Порядок выполнения работы
1. Внимательно ознакомиться с установкой (рис.8.2). Перемещая уравновешивающий груз 1 вдоль линейки 2, добиться горизонтального положения оси гироскопа. 2.
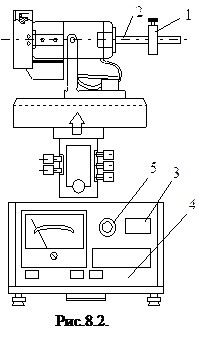 Включить прибор нажав клавишу СЕТЬ и убедиться в том, что все индикаторы 3 и 4 высвечивают цифру 0. Плавно вращая ручку 5 – РЕГУЛЯТОР СКОРОСТИ, установить число оборотов двигателя равным n =3000 об/ мин. При достижении заданного числа оборотов убедиться в отсутствии прецессии и заметить положение груза на линейке ( Включить прибор нажав клавишу СЕТЬ и убедиться в том, что все индикаторы 3 и 4 высвечивают цифру 0. Плавно вращая ручку 5 – РЕГУЛЯТОР СКОРОСТИ, установить число оборотов двигателя равным n =3000 об/ мин. При достижении заданного числа оборотов убедиться в отсутствии прецессии и заметить положение груза на линейке ( ). ).
3. Установить груз 1 на максимальное расстояние клавишу СБРОС, включить индикаторы времени и угла поворота. После поворота оси гироскопа на некоторый угол (около 30 – 1000) нажать клавишу СТОП. Записать показания времени t, угла поворота Таблица 8.1
4. По полученным данным определить угловую скорость прецессии
где 5. Из графика определить момент инерции гироскопа по формуле 6. Поместив груз в произвольное положение на линейке (кроме
Таблица 8.2
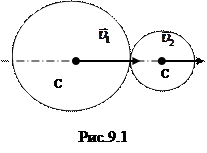
Контрольные вопросы 1. Как устроен гироскоп и каковы его основные свойства? Применения гироскопа. 2. Что называется прецессией? От чего зависит угловая скорость прецессии? 3. В чем заключается явление гироскопического эффекта? 4. При вращении твердого тела вокруг неподвижной оси куда направлены векторы момента силы, угловой скорости и углового ускорения? 5. Что называется моментом импульса? ИССЛЕДОВАНИЕ ЯВЛЕНИЯ УДАРА Лабораторная работа № 1.9 Цель работы: изучить некоторые вопросы теории удара твердых тел и на примере сталкивающихся шаров убедиться в применимости закона сохранения импульса к явлениям удара твердых тел, оценить длительность упругого удара. Оборудование: лабораторный стенд. Теоретическое введение Ударом называют явление конечного изменения скоростей твердых тел за весьма малый промежуток времени, происходящее при столкновениях. В процессе деформации тел при ударе возникают мгновенные (ударные) силы, величина которых весьма значительна. Мгновенные силы соударяющихся тел являются внутренними силами. Их импульсы за время продолжительности удара во много раз больше импульсов за то же время всех внешних сил, приложенных к системе тел. Поэтому в процессе удара влиянием внешних сил можно пренебречь и считать, что выполняются законы сохранения импульса и момента импульса. Общая нормаль к поверхности соударяющихся тел в точке их соприкосновения называется линией удара. Удар называется прямым, если скорости центров масс соударяющихся тел перед ударом параллельны линии удара. Удар называется центральным, если при ударе центры масс сталкивающихся тел лежат на линии удара. Удар двух любых шаров всегда будет центральным. Рассмотрим прямой центральный удар двух поступательно движущихся тел. Пусть скорости тел до удара υ1 и υ2, а после удара скорости u 1 и u 2 и направлены вдоль прямой – оси ОХ, проходящей через центры инерции тел (рис.9.1).
В проекциях на эту ось по закону сохранения импульса можно записать:
где m1 и m2 – массы тел. Величины υ 1 и υ 2, u 1 и u 2 – положительны или отрицательны в зависимости от того, как направлен соответствующий вектор скорости (вдоль положительного направления оси ОХ или в противоположную сторону). Для характеристики упругости (пластичности) ударяющихся тел, вводят коэффициент восстановления k, равный модулю отношения разностей скоростей тел в конце и в начале удара:
Последний результат следует из того, что до удара должно быть
получим:
Уменьшение кинетической энергии тел в результате удара равно
Из выражения(9.3) видно, что ΔТ≤0, т.е. кинетическая энергия тел либо уменьшается при ударе, либо остается неизменной. Часть механической энергии при 0 < k < 1 преобразуется во внутреннюю энергию системы. Если ударные силы потенциальны, то удар называется абсолютно упругим, или просто упругим. При этом k =1 и скорости тел после удара будут равны:
Удар называется неупругим (абсолютно неупругим), если после него тела движутся с одинаковой скоростью, т.е u 1= u 2= u и k =0. В этом случае скорость тел в неподвижной системе равна
Во всех остальных случаях удар называется не вполне упругим и 0< k <1.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.108 (0.009 с.) |

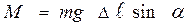 ,
,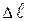 - смещение груза m от положения, соответствующего равновесию
- смещение груза m от положения, соответствующего равновесию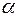 - угол наклона оси гироскопа к вертикали.
- угол наклона оси гироскопа к вертикали.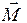 перпендикулярно силе тяжести mg и вектору момента импульса гироскопа L, т.е.
перпендикулярно силе тяжести mg и вектору момента импульса гироскопа L, т.е.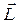 за время
за время 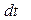 получит приращение
получит приращение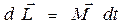 , (8.1)
, (8.1)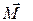 , т.е. перпендикулярно
, т.е. перпендикулярно 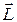 . В результате этого вертикальная плоскость, проходящая через ось гироскопа, повернется на угол
. В результате этого вертикальная плоскость, проходящая через ось гироскопа, повернется на угол 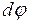 . Поскольку при этом взаимное расположение векторов
. Поскольку при этом взаимное расположение векторов 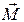 и
и 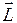 не изменится, то вектор
не изменится, то вектор 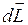 будет все время перпендикулярным к
будет все время перпендикулярным к  . В итоге ось гироскопа будет непрерывно поворачиваться вокруг вертикали, совершая конусообразное движение. Такое движение называется прецессией. Угловая скорость прецессии равна
. В итоге ось гироскопа будет непрерывно поворачиваться вокруг вертикали, совершая конусообразное движение. Такое движение называется прецессией. Угловая скорость прецессии равна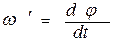 , (8.2)
, (8.2)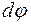 вокруг вертикальной оси может быть представлен как
вокруг вертикальной оси может быть представлен как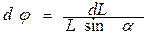 .
.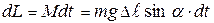 и
и  , то придем к следующей формуле:
, то придем к следующей формуле: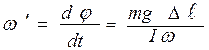 . (8.3)
. (8.3) видно, что скорость прецессии не зависит от угла наклона оси гироскопа по отношению к горизонту.
видно, что скорость прецессии не зависит от угла наклона оси гироскопа по отношению к горизонту. от точки опоры С гироскопа. Убедиться в том, что ось гироскопа сохраняет горизонтальное положение, но появляется её вращение вокруг вертикали, т.е. прецессия. Нажав
от точки опоры С гироскопа. Убедиться в том, что ось гироскопа сохраняет горизонтальное положение, но появляется её вращение вокруг вертикали, т.е. прецессия. Нажав и заметить направление прецессии. Аналогичным образом, смещая каждый раз груз на 1 см по линейке, произвести не менее 10 измерений соответствующих значений
и заметить направление прецессии. Аналогичным образом, смещая каждый раз груз на 1 см по линейке, произвести не менее 10 измерений соответствующих значений  и t. Результаты измерений занести в табл. 8.1.
и t. Результаты измерений занести в табл. 8.1. м
м
 0
0
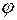 ,
рад
,
рад
 c
c
 1/с
1/с
 м
м
 ,
H·м
,
H·м
 ,
Дж·с
,
Дж·с
 ,
кг·м2
,
кг·м2
 (угол
(угол  выразить в радианах) и построить график зависимости угловой скорости прецессии от величины внешнего момента силы
выразить в радианах) и построить график зависимости угловой скорости прецессии от величины внешнего момента силы ,
,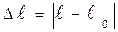 .
. , где
, где 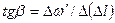
 ) и не меня его положения, исследовать зависимость, скорости прецессии
) и не меня его положения, исследовать зависимость, скорости прецессии  от скорости вращения гироскопа
от скорости вращения гироскопа  вокруг своей оси. Результаты измерений занести в табл. 8.2. Построить график зависимости
вокруг своей оси. Результаты измерений занести в табл. 8.2. Построить график зависимости .
. с
с
 , 1/с
, 1/с
 ,1/с
,1/с

 . (9.1)
. (9.1) (иначе удара не произойдет), а после удара будет
(иначе удара не произойдет), а после удара будет 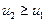 , в силу непроницаемости тел. Решая систему неравенств:
, в силу непроницаемости тел. Решая систему неравенств: ,
, ,
, . (9.2)
. (9.2) . (9.3)
. (9.3)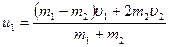 , и
, и  (9.4)
(9.4) . (9.5)
. (9.5)


