Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание установки и методика измеренияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Маятник Максвелла представляет собой ролик (маховичок), который закреплен на оси и бифилярным способом горизонтально подвешен на неподвижной балке. На ролик маятника могут накладываться сменные металлические кольца, позволяющие изменить момент инерции системы (рис.4.1)
Рис.4.1 Маятник Максвелла является основной частью лабораторной установки, содержащей электромагнит, фотодатчики и электронный измеритель времени. Если сначала поднять маятник до некоторой высоты, наматывая нити подвеса виток к витку на валик путем его поворота, а затем отпустить, то он достаточно длительное время будет совершать периодические движения вниз-вверх. Отсюда, собственно, и название системы «маятник». В момент достижения маятником нижнего положения происходит упругий удар, в результате которого скорость поступательного движения получает противоположное направление, практически не меняя своей величины. Направление же вращательного движения остается прежним. В результате этого нити подвеса будут навиваться на ось в противоположном направлении, и маятник будет подниматься вверх. Процесс перемещения маятника вниз-вверх будет многократным. Если пренебрегать силами сопротивления, то маятник Максвелла в целом можно рассматривать как консервативную систему, а его движение – соответствующее закону сохранения механической энергии. Пусть m – масса маятника, I – его момент инерции. Положение маятника в текущий момент времени будем определять координатой x центра масс относительно его начального положения x = 0 в момент t = 0. На рис.4.2 указаны основные силы, действующие на тело маятника, и направления его движений. Считаем, что нити подвески маятника практически вертикальны. Заменяем действие двух нитей на тело их суммарной реакцией N. На основании законов динамики плоско-параллельного движения тела имеем два уравнения:
Здесь a –ускорение вертикального перемещения тела вниз, Из данной системы уравнений определяем
и координату При начальных условиях
Для консервативной системы полная механическая энергия Е = Т + U = const. Отсюда следует, что приращение кинетической энергии системы равно убыли её потенциальной энергии, т.е. Применительно к маятнику
Следовательно,
Высоте h задается определенное значение, которое в процессе всех опытов остается неизменным. Варьируя величиной момента инерции маятниковой системы при помощи сменных колец, будем путем измерений получать соответствующие промежутки времени t. Из равенства (4.7) для квадрата времени получим
где D = 2 R - диаметр навивки нитей подвеса, а для момента инерции получим следующее соотношение
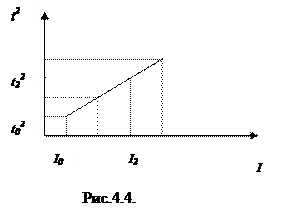
Отсюда следует, что выполнение данной лабораторной работы будет состоять из двух пунктов: а) убедиться в справедливости соотношения (4.8), т.е. в действии закона сохранения механической энергии. При этом для заданных значений момента инерции системы измеряется время опускания как нагруженного, так и ненагруженного маятника до крайнего нижнего положения. В результате этих измерений получим последовательность точек (Iк, t2к). Нанося эти точки на плоскость t2 (I), мы увидим линейную зависимость t2 от I, примерно изображенную на рис.4.4. Заметим, что погрешность полученных результатов не должна превышать 2 - 4%.
б) убедившись в непосредственном действии закона сохранения энергии, в этом пункте предстоит определить момент инерции нескольких металлических колец, накладываемых на ролик маятника. По данным измерений времени и известным значениям других величин по формуле
найдем момент инерции кольца. Здесь m0 и I0 - собственные значения массы и момента инерции маятника соответственно, а m -масса кольца. Порядок выполнения работы 1. Изучить лабораторную установку и её действие. 2. Согласовать с преподавателем величину h (h - расстояние между исходным верхним и нижним положениями маятника при его опускании). Записать значения характери- стик маятника. 3. Включить прибор в сеть и нажать клавишу «Пуск». При этом произойдет обнуление измерителя времени и включение электромагнита, а также начнут светиться фотоэлектрические датчики. 4. Аккуратно навить нити подвеса на валик маятника до его прилипания к электромагниту. Навивка нитей должна быть симметричной относительно ролика и осуществляется за концы валика. 5. Нажатием клавиши «Сброс» маятник освобождается от электромагнита и запускается индикатор времени, а маятник начинает опускаться. В момент, когда маятник достигает крайнего нижнего положения, измеритель времени прекращает свою работу. При этом индикатор измерителя будет показывать время опускания маятника. 6. Усредненные результаты нескольких измерений и соответствующих расчетов занести в таблицы 4.1 и 4.2. В табл. 4.1 по пункту а) Таблица 4.1
по пункту б) в табл.4.2. Таблица 4.2
Значения массы представить в граммах, момента инерции в г ·см2. Контрольные вопросы
1. Динамические уравнения поступательного и вращательного движения твердого тела. 2. Понятия момента инерции и момента импульса тела относительно точки и оси. 3. Сущность метода измерения момента инерции металлических колец при помощи маятника Максвелла. 4. Закон сохранения момента импульса.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 542; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.011 с.) |



 , (4.1)
, (4.1) . (4.2)
. (4.2)
 - угловое ускорение вращательного движения тела вокруг центральной оси О.
- угловое ускорение вращательного движения тела вокруг центральной оси О.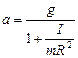 , (4.3)
, (4.3) . (4.4)
. (4.4)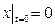 и
и 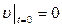 , при этом скорость поступательного движения и кинетическая энергия тела к моменту времени t соответственно будут равны
, при этом скорость поступательного движения и кинетическая энергия тела к моменту времени t соответственно будут равны , (4.5)
, (4.5) . (4.6)
. (4.6) .
. (Т1=0, Т2=Т), -
(Т1=0, Т2=Т), -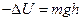 , где h – высота на которую опустился маятник за время t.
, где h – высота на которую опустился маятник за время t.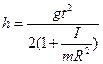 . (4.7)
. (4.7) , (4.8)
, (4.8) . (4.9)
. (4.9)