
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К лабораторному практикуму по механикеСодержание книги
Поиск на нашем сайте
К лабораторному практикуму по механике для студентов первого курса всех специальностей
Воронеж 2005 Составители: канд. физ.-мат. наук Евсюков В. А., канд. физ.-мат. наук А.Г. Москаленко, канд. физ.-мат. наук Н.В. Матовых, канд. физ.-мат. наук И. А. Сафонов, канд. физ.-мат. наук А.Ф. Татаренков, канд. пед. наук О. С.Хабарова.
УДК 531 (07) Методические указанияк выполнению лабораторного практикума по механике для студентов первого курса всех специальностей/ Воронеж. гос. техн. ун-т; Воронеж, 2005, 58 с.
Методические указания содержат описание методик измерения, приборов и порядок выполнения лабораторных работ № 1.1 - 1.10, поставленных и выполняемых в учебных лабораториях ВГТУ. Предназначено для студентов всех специальностей и всех форм обучения.
Ил. 20. Библиогр. 6 назв.
Рецензент канд. физ.- мат.наук А.А. Долгачёв
Ответственный за выпуск зав. кафедрой общей физики механико-технологического профиля, профессор В.С.Железный
Печатается по решению редакционно–издательского совета Воронежского государственного технического университета
© Воронежский государственный
1. ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ НА МАШИНЕ АТВУДА
Лабораторная работа 1.1. Приборы и принадлежности: машина Атвуда, миллисекундомер, набор грузов и перегрузков. Цель работы: ознакомление с методикой измерения ускорения свободного падения и проверка законов динамики. 1.1. Описание прибора и методика измерений
Рис 1.1 Машина Атвуда предназначена для исследования движения тел в поле земного тяготения. Устройство машины изображено на рис.1.1. Блок
где угловое ускорение блока; Решение данной системы уравнений даёт следующее выражение для g:
Для определения ускорения
где В конце пути S 1 перегрузок Измеряя путь S2 и время t равномерного движения правого груза на этом пути, можно определить скорость u, а затем по формуле (1.5) ускорение. При этом:
Теперь легко получить формулу для ускорения свободного падения:
Пути S1 и S2 определяются по шкале прибора. Порядок выполнения работы 1. Убедиться, что прибор установлен строго по вертикали и правый груз М свободно проходит сквозь съемное кольцо 2. Включить прибор клавишей СЕТЬ, при этом клавиша СБРОС должна быть отжата, а клавиша ПУСК нажата. 3. Положить на правый груз перегрузок и поднять груз вверх, совместив нижнюю грань груза с чертой, нанесенной на верхнем кронштейне. 4. Отжать клавишу ПУСК, зафиксировав тем самым груз в верхнем положении. 5. Измерить по миллиметровой шкале на стойке прибора пути равноускоренного S 1 и равномерного S2 движений груза. 6. Нажать клавишу ПУСК. 7.Записать измеренное миллисекундомером время движения груза на пути S2. 8. Нажать клавишу СБРОС и проверить обнуление показаний прибора и выключение электромагнита. 9. Поднять правый груз вверх и повторить опыт. Измерения проводить не менее пяти раз, после чего определить среднее значение времени движения груза на участке S 2 при заданном перегрузке. Данные измерений внести в табл. 1.1. 10. Определить по формуле (6) ускорение системы a, подставив среднее значение времени t, и полученный результат записать в табл. 1.1. 11. Рассчитать по формуле (1.7) значение ускорения свободного падения g и записать в табл. 1.1. 12. Повторить опыт дважды, взяв перегрузки в наборе из 2 колец другой массы. Результаты записать в таблицы, аналогичные табл. 1.1, и рассчитать соответствующие значения g. Таблица 1.1
13. Сделать оценку погрешности полученного результата.
Контрольные вопросы 1. Определения (понятия) кинематических характеристик движущейся точки. 2. Закон движения точки в векторной и координатной формах. 3. Сформулируйте законы динамики материальной точки (поступательного движения твердого тела). 4. Закон всемирного тяготения. Понятие напряженности и потенциала гравитационного поля. 5. Сила тяжести и вес тела. Состояние невесомости. 6. Зависимость ускорения свободного падения от географической широты местности.
Лабораторная работа № 1.2.
Цель работы: исследовать деформацию кручения цилиндрического тела и установить связь между крутящим моментом и углом закручивания. Определить модуль сдвига образца. Оборудование: крутильный маятник, измеритель периода крутильных колебаний системы, набор металлических дисков с известными моментами инерции, стальная проволока, электромагнит. Теоретическое введение Под действием приложенных сил всякое твердое тело деформируется, т.е. изменяет свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, то деформация называется упругой. В противном случае – неупругой (пластической). Упругие деформации имеют место в том случае, если деформирующая сила не превосходит некоторую определенную для каждого конкретного тела предельную силу Fпр. При деформациях происходит смещение частиц, находящихся в узлах кристаллических решеток твердых тел, из первоначальных положений равновесия в новые. Этому препятствуют силы электромагнитного взаимодействия между частицами, вследствие чего в деформированном теле возникают упругие внутренние силы, которые уравновешивают внешние силы, приложенные к телу. Пусть на выделенный элемент поверхности dS некоторого сечения тела действует упругая сила dFупр, а dFn и dFτ – нормальная и касательная составляющие этой силы (рис. 2.1). Величину σ = dFn/dS называют нормальным напряже- нием в окрестности заданной точки, а величину τ = dFτ/dS – касательным напряжением. Согласно определению единицей измерения напряжения в системе СИ является [ σ ] = [ τ ] = = H/м2 = Па.
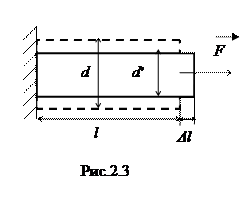
Мерой деформации растяжения-сжатия является относительное удлинение (сжатие) ε = Δ l / l (рис.2.2а).
Мерой деформации сдвига является угол сдвига γ, выраженный в радианах (рис.2.2б). Для малых деформаций γ ≈ tgγ = a/b, где а – абсолютный сдвиг, b - расстояние между параллельными плоскостями слоя. Относительные деформации ε и γ – безразмерные величины. Иногда их представляют в %. Для малых (упругих) деформаций растяжения-сжатия и сдвига, как показывают опыты, существует линейная связь между напряжением и соответствующей относительной деформацией: σ = Еε, (2.1) τ = Gγ (2.2)
Между модулями упругости G и E имеется связь:
Величину μ, равную отношению относитель- ного сужения (расшире- ния) Δd/d к относительному продольному удлинению (сжатию) называют коэффициентом Пуассона:
где Δd= d - d َ ′. Рассмотрим деформации, вызываемые кручением твердого цилиндрического тела. Кручением называется деформация образца с одним закрепленным концом (а может быть условно) под действием пары сил, плоскость которой перпендикулярна оси образца. Кручение состоит в относительном повороте параллельных друг другу сечений, проведенных перпендикулярно к оси образца. Деформация кручения является неоднородной. Она увеличивается при удалении от оси поворотов элементов образца. Закон Гука для деформации кручения записывается в виде
Постоянная кручения показывает, какой момент сил нужно приложить, чтобы закрутить проволоку на угол в 1 рад. В отличие от модулей Юнга и сдвига эта величина зависит не только от материала, но и от геометрических размеров проволоки. Деформацию кручения можно свести к деформации сдвига. Получим выражение для постоянной кручения ¦. Стержень (рис.2.4) можно представить состоящим из множества цилиндрических оболочек (трубок), каждая из которых характеризуется радиусом r, длиной L и толщиной dr. Площадь основания трубки dS = 2p r dr, (2.6) а момент касательных упругих сил, действующих в этом основании,
где Каждый продольный элемент цилиндрической трубки поворачивается на угол
По закону Гука для сдвига получим
Итак, момент сил, действующих на цилиндрическую трубку, равен
C
φ L
O
Полный же момент сил, действующих на проволоку (стержень) радиуса R, найдется интегрированием выражения (2.10):
Имея соотношения (2.5) и (2.11), получим выражение для постоянной кручения образца
Экспериментально модуль кручения можно измерить, наблюдая крутильные колебания маятника. . Порядок выполнения работы 1. Убедиться, что крутильный маятник в исходном состоянии имеет вертикальное положение. В противном случае произвести выравнивание прибора с помощью регулируемых ножек основания. 2. Установить какой-либо инерционный диск в рамку маятника и измерить период колебаний, повторяя данную процедуру 3-5 раз. По данным этих измерений найти среднее значение периода Т1. 3. Установить второй инерционный диск в рамку маятника, не снимая первый. Произвести 3-5 измерений периода и найти его среднее значение Т2. 4. По формуле (2.20) найти модуль сдвига стальной проволоки. Результаты измерений и расчетов записать в таблицу 2.1. Таблица 2.1
Контрольные вопросы
Лабораторная работа № 1.3
Цель работы: изучение законов динамики вращательного движения и экспериментальное определение момента инерции тел вращения с помощью трифилярного подвеса. Принадлежности: трифилярный подвес, секундомер, штангенциркуль, образцы для измерений, линейка.
Порядок выполнения работы 1. Записать для данной установки постоянные величины, указанные в табл. 3.1. Таблица 3.1.
Масса m* диска и число полных колебаний n задаются преподавателем. 2. Привести пустую платформу в состояние крутильных колебаний, измерить время заданного преподавателем числа полных колебаний, рассчитать период колебаний. Полученные результаты занести в табл. 3.2. Аналогичные измерения и расчёты сделать для нагруженной платформы. 3. Вычислить моменты инерции J0 и J1 ненагруженной и нагруженной платформы. Определить момент инерции измеряемого тела по формуле J = J1- J0. Рассчитать погрешности эксперимента и записать окончательный результат.
Таблица 3.2.
4. Рассчитать теоретическое значение момента инерции исследуемого тела, имеющего форму диска с соосным круглым отверстием:
Здесь R 1 и R 2 – внешний и внутренний радиусы диска, m* - его масса. 5. Полученные в п. 4 данные сравнить с результатами опыта. Оценить в процентах отклонение значения момента инерции, полученное в опыте, от теоретически рассчитанной величины.
Контрольные вопросы
ИЗМЕРЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА МАКСВЕЛЛА Лабораторная работа № 1.4.
Цель работы: экспериментально убедиться в справедливости закона сохранения энергии консервативной системы во время движения, а затем на основе этого закона измерить моменты инерции некоторых металлических колец при помощи маятника Максвелла. Оборудование: маятник Максвелла, набор металличе- ских колец с известными и неизвестными моментами инерции.
Порядок выполнения работы 1. Изучить лабораторную установку и её действие. 2. Согласовать с преподавателем величину h (h - расстояние между исходным верхним и нижним положениями маятника при его опускании). Записать значения характери- стик маятника. 3. Включить прибор в сеть и нажать клавишу «Пуск». При этом произойдет обнуление измерителя времени и включение электромагнита, а также начнут светиться фотоэлектрические датчики. 4. Аккуратно навить нити подвеса на валик маятника до его прилипания к электромагниту. Навивка нитей должна быть симметричной относительно ролика и осуществляется за концы валика. 5. Нажатием клавиши «Сброс» маятник освобождается от электромагнита и запускается индикатор времени, а маятник начинает опускаться. В момент, когда маятник достигает крайнего нижнего положения, измеритель времени прекращает свою работу. При этом индикатор измерителя будет показывать время опускания маятника. 6. Усредненные результаты нескольких измерений и соответствующих расчетов занести в таблицы 4.1 и 4.2. В табл. 4.1 по пункту а) Таблица 4.1
по пункту б) в табл.4.2. Таблица 4.2
Значения массы представить в граммах, момента инерции в г ·см2. Контрольные вопросы
1. Динамические уравнения поступательного и вращательного движения твердого тела. 2. Понятия момента инерции и момента импульса тела относительно точки и оси. 3. Сущность метода измерения момента инерции металлических колец при помощи маятника Максвелла. 4. Закон сохранения момента импульса. Порядок выполнения работы
1. Убедиться в вертикальной установке прибора. 2. Установить груз с минимальным значением массы. 3. Измерить штангенциркулем диаметры большего шкива D и меньшего шкива d. 4. Подключить сетевой кабель в розетку и нажать клавишу СЕТЬ. 5. Нажать клавишу ПУСК и намотать нить на малый шкив, вращая маятник против часовой стрелки. При этом рукой держаться только за ось, а не за стержень. Груз поднимать до такой высоты, чтобы нижняя грань груза была на одном уровне с риской на верхнем кронштейне (тело груза не должно перекрывать окошко фотодатчика). 6. Отжать клавишу ПУСК и убедиться, что электромагнит удерживает груз в фиксированном положении, а на секундомере – нули. 7. Нажать клавишу ПУСК. Электромагнит отключится, и груз станет опускаться вниз, вращая маятник. При достижении грузом нижнего фотодатчика происходит автоматическая остановка секундомера и включается электромагнит. 8. После записи времени опускания в табл. 5.1 немедлен- но нажать клавишу СБРОС. При этом отключается электромагнит и обнуляется секундомер. Установка готова к повторению опыта. 9. Измерение времени для каждого груза проводят три раза и вычисляют среднее значение. Опыт проделать не менее чем с пятью грузами. Данные занести в табл. 5.1. Таблица 5.1
10. Подставив среднее значение времени, по формулам (5.1) и (5.2 ) находят М и e для каждого груза. Строят график 11. По тангенсу угла наклона прямой 12. Все опыты повторить с большим шкивом, не забывая вращать маятник против часовой стрелки только за ось, а не за стержни. Заполнить аналогичную таблицу для второго шкива. 13. Построить второй график
15. По формуле (5.3) находят момент инерции ненагруженного маятника I 0: 16. По указанию преподавателя рассчитать погрешности, пользуясь методом наименьших квадратов (для этого можно использовать стандартную прикладную программу для ЭВМ в дисплейном классе).
Контрольные вопросы 1. Утверждение и доказательство теоремы Штейнера. 2. Что есть момент силы относительно неподвижной точки заданной оси? 3. Какая связь между линейным и угловым ускорениями точки тела? 4. Обосновать уравнение динамики вращательного движения твердого тела. 5. Определить моменты инерции однородного сплошного цилиндра высотой h и радиусом R относительно его главных центральных осей. Масса цилиндра М.
Порядок выполнения работы
1. Записать в табл. 6.1. все постоянные для данной установки (прибора) величины. Таблица 6.1
2. Отрегулировать длину нитей так, чтобы направление оси цилиндра было горизонтально и перпендикулярно линии, соединяющей обе точки подвеса. Надо следить за тем, чтобы нити подвеса не перекручивались. Установить шкалу параллельно оси цилиндра и подготовить «пушку» к выстрелу. Убедившись в том, что пуля, вылетевшая из «пушки», может попасть в точку на оси цилиндра, произвести пять выстрелов каждой пулей и полученные результаты записать в табл. 6.2. 3. Вычислить по формуле (6.10) среднее значение скорости каждой пули по среднему значению смещения стрелки из положения равновесия. 4. Рассчитать погрешности и записать окончательный результат. Таблица 6.2
Контрольные вопросы 1. Что называется импульсом и моментом импульса материальной точки и твердого тела? Направления этих величин. 2. Можно ли к системе «пуля-цилиндр» применить закон сохранения количества движения? Закон сохранения механической энергии? 3. Пуля массой m, летящая горизонтально со скоростью v, попадает в баллистический маятник длиной l и массой M и застревает в нем. Определите угол отклонения маятника.
7. ОПРЕДЕЛЕНИЕ СКОРОСТИ СНАРЯДА С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО КРУТИЛЬНОГО МАЯТНИКА
Лабораторная работа 1.7.
Цель работы: экспериментальное изучение законов сохранения. Приборы и принадлежности: крутильный маятник, набор снарядов, измерительная линейка, весы.
Порядок выполнения работы
Определение скорости полета снаряда производится в следующем порядке: 1. Максимально приблизить грузы (11) друг к другу ( R1= = min ). 2. Обнулить маятник, т. е. установить маятник в положение, чтобы черта на чашечке совпадала с нулем шкалы на прозрачном экране. 3. Выстрелить снаряд. 4. Визуально зафиксировать максимальный угол jm отклонения маятника. 5. Включить и обнулить счетчик времени нажатием кнопки СБРОС. 6. Отклонить маятник на угол 7. Измерить время 10 колебаний и вычислить период T1 ( T1 = t /10 ). 8. Максимально отдалить друг от друга грузы (11) ( R 2 = = max ) и повторить действия по п.п. 2, 5 и 6. 9. Измерить время 10 колебаний и вычислить Т2. 10. Скорость снаряда вычислить по формуле (7.15). 11. Измерения скорости снаряда повторить не менее трех раз. По данным этих измерений определить среднее значение скорости и ошибку измерений.
Контрольные вопросы 1. Какое направление имеет момент импульса твердого тела при вращении? 2. Дайте определение момента инерции. Сформулируйте теорему Штейнера 3. Сформулируйте закон сохранения момента импульса и энергии при вращательном движении. 4. Дайте определение углового ускорения и запишите основное уравнение динамики вращательного движения. 5. Вычислить момент инерции однородного сплошного конуса относительно его оси симметрии, если известны его масса и радиус основания.
Описание гироскопа
Гироскоп представляет собой массивное симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии. Эту ось называют осью гироскопа.
              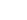                  Рассмотрим гироскоп с одной неподвижной точкой О на его оси. (рис.8.1). Точку 0 называют точкой опоры, или центром подвеса гироскопа. Если центр подвеса гироскопа совпадает с его центром масс, то результирующий момент сил тяжести всех частей гироскопа Рассмотрим гироскоп с одной неподвижной точкой О на его оси. (рис.8.1). Точку 0 называют точкой опоры, или центром подвеса гироскопа. Если центр подвеса гироскопа совпадает с его центром масс, то результирующий момент сил тяжести всех частей гироскопа  относительно 0 равен нулю. Такой гироскоп называется уравновешенным. После приведения уравновешенного гироскопа в быстрое вращение его ось будет сохранять свое направление в пространстве и сопротивляться всяким попыткам изменить это направление. Смещая груз m в ту или иную сторону от положения равновесия, вызываем разбаланс системы, в результате чего возникает вращающий момент относительно 0 равен нулю. Такой гироскоп называется уравновешенным. После приведения уравновешенного гироскопа в быстрое вращение его ось будет сохранять свое направление в пространстве и сопротивляться всяким попыткам изменить это направление. Смещая груз m в ту или иную сторону от положения равновесия, вызываем разбаланс системы, в результате чего возникает вращающий момент  , обусловленный действием силы тяжести mg груза. Величина вращающего момента , обусловленный действием силы тяжести mg груза. Величина вращающего момента  будет равна будет равна
где m – масса уравновешивающего груза; системы маховик – груз; Направление момента В случае вращающегося гироскопа его момент импульса
совпадающее по направленное с вектором
где поворот оси гироскопа
Если учесть, что
Из выражения для
Порядок выполнения работы
1. Внимательно ознакомиться с установкой (рис.8.2). Перемещая уравновешивающий груз 1 вдоль линейки 2, добиться горизонтального положения оси гироскопа. 2.
 Включить прибор нажав клавишу СЕТЬ и убедиться в том, что все индикаторы 3 и 4 высвечивают цифру 0. Плавно вращая ручку 5 – РЕГУЛЯТОР СКОРОСТИ, установить число оборотов двигателя равным n =3000 об/ мин. При достижении заданного числа оборотов убедиться в отсутствии прецессии и заметить положение груза на линейке ( Включить прибор нажав клавишу СЕТЬ и убедиться в том, что все индикаторы 3 и 4 высвечивают цифру 0. Плавно вращая ручку 5 – РЕГУЛЯТОР СКОРОСТИ, установить число оборотов двигателя равным n =3000 об/ мин. При достижении заданного числа оборотов убедиться в отсутствии прецессии и заметить положение груза на линейке ( ). ).
3. Установить груз 1 на максимальное расстояние клавишу СБРОС, включить индикаторы времени и угла поворота. После поворота оси гироскопа на некоторый угол (около 30 – 1000) нажать клавишу СТОП. |


 технический университет, 2005
технический университет, 2005
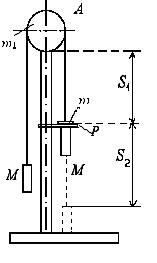
 массой
массой  может свободно вращаться вокруг оси, укрепленной в верхней части стойки. Через блок перекинута нить, к концам которой подвешены два груза равных масс
может свободно вращаться вокруг оси, укрепленной в верхней части стойки. Через блок перекинута нить, к концам которой подвешены два груза равных масс  . Если на правый груз поместить один или несколько перегрузков, то представленная самой себе система грузов начнет двигаться с ускорением. В начале опыта блок
. Если на правый груз поместить один или несколько перегрузков, то представленная самой себе система грузов начнет двигаться с ускорением. В начале опыта блок 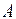 фиксируется с помощью электромагнита. При выключении тока, текущего через электромагнит, блок освобождается и система приходит в движение. На основании законов динамики поступательного и вращательного движений получим следующие уравнения:
фиксируется с помощью электромагнита. При выключении тока, текущего через электромагнит, блок освобождается и система приходит в движение. На основании законов динамики поступательного и вращательного движений получим следующие уравнения: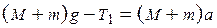 , (1.1)
, (1.1)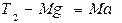 , (1.2)
, (1.2) , (1.3)
, (1.3)
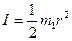 - момент инерции блока
- момент инерции блока  ;
; 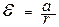 -
- и
и  - силы натяжения правой и левой частей нити; m – масса перегрузка.
- силы натяжения правой и левой частей нити; m – масса перегрузка.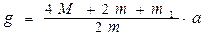 . (1.4)
. (1.4) грузов рассмотрим движение правого груза на участке пути
грузов рассмотрим движение правого груза на участке пути 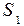 . Так как начальная скорость равна нулю, то
. Так как начальная скорость равна нулю, то , (1.5)
, (1.5) - конечная скорость на участке
- конечная скорость на участке 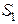 .
.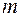 снимается с правого груза
снимается с правого груза 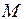 неподвижным кольцом
неподвижным кольцом 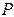 , после чего система грузов начинает двигаться равномерно со скоростью, приобретенной в конце участка S1 .
, после чего система грузов начинает двигаться равномерно со скоростью, приобретенной в конце участка S1 . . (1.6)
. (1.6)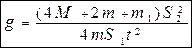 . (1.7)
. (1.7)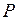 .
. Нормальные напряжения вызываются деформациями растяжения-сжатия тела, а касательные – смещением плоских слоев твердого тела параллельно некоторой плоскости сдвига без их искривления и изменения размеров. В связи с этим выделяют два основных вида деформации твердого тела: – растяжения - сжатия и деформацию сдвига. Изгиб, кручение и более сложные деформации относятся либо к одному из двух основных неоднородных деформаций, либо к их наложению.
Нормальные напряжения вызываются деформациями растяжения-сжатия тела, а касательные – смещением плоских слоев твердого тела параллельно некоторой плоскости сдвига без их искривления и изменения размеров. В связи с этим выделяют два основных вида деформации твердого тела: – растяжения - сжатия и деформацию сдвига. Изгиб, кручение и более сложные деформации относятся либо к одному из двух основных неоднородных деформаций, либо к их наложению.

 Величины Е и G называют модулями упругости материала. Первый модуль Е – нормальным (модулем Юнга), второй G – модулем сдвига. Из (2.1) и(2.2) видно, что размерность модулей упругости та же, что и для напряжения.
Величины Е и G называют модулями упругости материала. Первый модуль Е – нормальным (модулем Юнга), второй G – модулем сдвига. Из (2.1) и(2.2) видно, что размерность модулей упругости та же, что и для напряжения.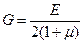 . (2.3)
. (2.3)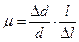 , (2.4)
, (2.4)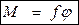 , (2.5) где ƒ - постоянная кручения,
, (2.5) где ƒ - постоянная кручения, 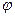 - абсолютный угол кручения образца.
- абсолютный угол кручения образца. , (2.7)
, (2.7) - напряжение сдвига в этом сечении.
- напряжение сдвига в этом сечении. . (2.8)
. (2.8)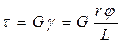 . (2.9)
. (2.9)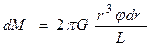 . (2.10)
. (2.10) O
O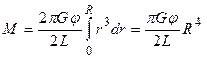 . (2.11)
. (2.11)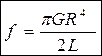 . (2.12)
. (2.12)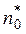
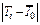 , c
, c
 c2
c2
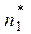
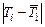 , c
, c
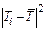 c2
c2
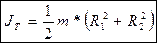 ,
,
 . Это должна быть прямая линия.
. Это должна быть прямая линия. определить среднее значение момента инерции I.
определить среднее значение момента инерции I. и определить I2. 14. Вычислить среднее арифметическое значение момента инерции нагруженного маятника:
и определить I2. 14. Вычислить среднее арифметическое значение момента инерции нагруженного маятника: .
.

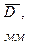
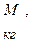
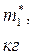
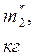
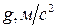
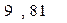

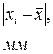
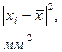
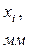
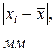
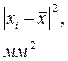
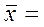
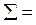

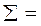
 , нажать кнопку СБРОС и отпустить одновременно с маятником.
, нажать кнопку СБРОС и отпустить одновременно с маятником.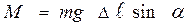 ,
,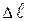 - смещение груза m от положения, соответствующего равновесию
- смещение груза m от положения, соответствующего равновесию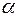 - угол наклона оси гироскопа к вертикали.
- угол наклона оси гироскопа к вертикали.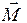 перпендикулярно силе тяжести mg и вектору момента импульса гироскопа L, т.е.
перпендикулярно силе тяжести mg и вектору момента импульса гироскопа L, т.е.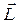 за время
за время 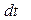 получит приращение
получит приращение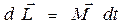 , (8.1)
, (8.1)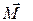 , т.е. перпендикулярно
, т.е. перпендикулярно 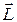 . В результате этого вертикальная плоскость, проходящая через ось гироскопа, повернется на угол
. В результате этого вертикальная плоскость, проходящая через ось гироскопа, повернется на угол 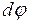 . Поскольку при этом взаимное расположение векторов
. Поскольку при этом взаимное расположение векторов 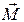 и
и 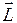 не изменится, то вектор
не изменится, то вектор 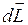 будет все время перпендикулярным к
будет все время перпендикулярным к  . В итоге ось гироскопа будет непрерывно поворачиваться вокруг вертикали, совершая конусообразное движение. Такое движение называется прецессией. Угловая скорость прецессии равна
. В итоге ось гироскопа будет непрерывно поворачиваться вокруг вертикали, совершая конусообразное движение. Такое движение называется прецессией. Угловая скорость прецессии равна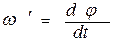 , (8.2)
, (8.2)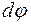 вокруг вертикальной оси может быть представлен как
вокруг вертикальной оси может быть представлен как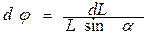 .
.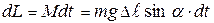 и
и  , то придем к следующей формуле:
, то придем к следующей формуле: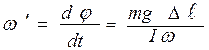 . (8.3)
. (8.3) видно, что скорость прецессии не зависит от угла наклона оси гироскопа по отношению к горизонту.
видно, что скорость прецессии не зависит от угла наклона оси гироскопа по отношению к горизонту. от точки опоры С гироскопа. Убедиться в том, что ось гироскопа сохраняет горизонтальное положение, но появляется её вращение вокруг вертикали, т.е. прецессия. Нажав
от точки опоры С гироскопа. Убедиться в том, что ось гироскопа сохраняет горизонтальное положение, но появляется её вращение вокруг вертикали, т.е. прецессия. Нажав


