Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент импульса и закон его сохранения.Содержание книги
Поиск на нашем сайте
Момент импульса относительно неподвижной точки О - это физическая величина, определя емая векторным произведением L=[r*P], где r – радиус-вектор, P=mυ – импульс материальной точки. Момент импульса относительно неподви жной оси Z - это скалярная величина LZ, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки на данной оси. Значение момента импульса LZ не зависит от положения точки О на оси Z. Закон сохранения импульса: момент импульса твер дого тела относительно произвольной оси есть сумма моментов импульса отдельных частиц. Lя=Σ (от n до i) miυiri; υi=ωri; LZ=Σ (от n до i) miri2ω=ωΣ (от n до i) miri2=ωJя; dLя/dt=Jяdω/dt=MZ; dL/dt=M – это уравнение еще одна форма уравнения динамики вращательного движения. Для зам кнутой системы момент внешних сил =0. М=0 => L=const – закон сохранения момента импульса. Следствие изотропности пространства. Гироскоп – цилиндрическое твердое тело, быстро вращающееся вокруг оси симметрии. Имеет 3 степени свободы, если закреплен в одной непод вижной точке О, принадлежащей его оси, - центр подвеса гироскопа. Если центр подвеса совпада ет с центральной точкой, то такой гироскоп назы вается – уравновешенным, т.е. действие силы тя жести не вызывает изменения его вращения; в про тивном случае, гороскоп называется тяжелым. Прецессия с угловой скоростью. Ω – движение. Пусть момент импульсаL=Jω.dL/dt=M=[mgrC]= [rCmgL/Jω]=[ΩL]. Где Ω=mrCg/Jω. Чем больше угловая скорость собственного вращения гиро скопа, тем медленнее он прецессирует.
28. Деформация твердого тела. Закон Гука. Деформация – изменение формы и размеров тела под действием внешних сил. Классическая деформация – деформация, которая сохраняет ся в теле после прекращения действия внешних сил. Упругая деформация – если после прекра щения действия внешних сил тело принимает пе рвоначальную форму и объем. Закон Гук а (для других деформаций): относительная деформа ция пропорциональна напряжению. σ = Еξ, где Е – модуль Юнга (определяется напряжением, вызы вающим относительное удлинение, равное 1). ξ= σ /E=Δℓ/ℓ=F/ES, где S – поперечное сечение, F=ES Δℓ/ℓ=kΔℓ, ℓ - первоначальная длина, Δℓ - удлинен ие. Закон Гука: абсолютное удлинение (Δℓ) тела при упругой деформации пропорциональны де йствующей на тело силе. Все эти деформации могут быть сведены к одновременно происходя щим деформациям сжатия, растяжения и сдви га. Относительная деформация ξ – количествен ная мера, характеризующая степень деформа ции и определяемая: ξ=ℓ/Δℓ.
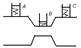
29. Связь между деформацией и напряжением Напряжение –физическая величина, определяе мая силой упругости, действующей на единицу S сечения: σ =Fупр/S. Если сила направлена по нор мали (к поверхности) – напряжение нормальное; по касательной – тангенсальное. Диаграмма на пряжений. Из графика видно, что линейная зави симость σ от ξ, установленная Гуком, выполняется лишь в малых пределах. При дальнейшем увели чении напряжения, деформация еще упругая, хо тя зависимость σ от ξ уже не линейная. До σy оста точные деформации не возникают. За пределом деформации возникают остаточные деформа ции. График возвращения тела в неравных состо яниях описывается прямой CF. Напряжения, при которых появляются заметная деформация (60,2%) называют пределом текучести (точка С на кривой). В области СD деформация возрастает без увеличения напряжения. Тело течет. Эта об ласть называется областью текучести (область пластической деформации). Материалы, для которых область текучести значительна, называются вязкими, для которых область текучес ти незначительна называют хрупкими. При дальне йшем растяжении за точку D приводит к разруше нию тела. Механическое напряжение, которое возникает до разрушения, называется пределом прочности (σβ) Одно и то же тело при кратковре менном действии сил проявит себя как хрупкое, а при длительных, но слабых силах является текучим
30. Закон всемирного тяготения. Между любыми двумя материальными точками действует сила взаимного притяженияпрямо про порциональная произведению масс этих точек и обратно пропорциональная квадрату расстояния между ними.F=γ*m1*m2/r², где γ-гравитационная постоянная.Сила F называется гравитационной или силой всемирного тяготения. В системе отсчета свя занной с Землей на всякое тело массой m действу ет сила тяжести P=mg.(P и g-векторы).Если пренеб речь суточным вращением Земли вокруг своей оси, то P=F=γ*M*m/r² (тело на поверхности земли). Вес тела – это сила, с которой тело вследствие тяготе ния Земли действует на опору или подвес и удержи вает его от свободного падения. Сила тяжести дейс твует всегда, а вес тела проявляется лишь тогда, ког да на тело кроме силы тяжести действуют другие силы.Невесомость – это состояние тела, при кото ром оно движется только под действием силы тяж.
31. Характеристики поля тяготения Напряженность поля тяготения – это физическая ве личина, определяемая силой действующей со сто роны поля на материальную точку единичной мас сы, и совпадает с направлением действия силы. dA=(-γ*m*M/R²)dR (1);A=∫|R2-R1|(γ*m*M/R²)dR=m* (γ*M/R1-γ*M/R2) (2);A=-∆П=-(П2-П1)=П1-П2;R2→∞; П2→0; П=-γ*m*M/R (3);Работа по перемещению тела массой m в поле тяготения на расстояние dR равно (1). При перемещении с расстояния R1 до R2 работа определяется по (2). Работа не зависит от траектории перемещения. Работа консерват ивных сил равняется изменению потенциальной энергии с обратным знаком.Потенциал поля тяготе ния – это физическая величина, определяемая поте нциальной энергией тела единичной массой в дан ной точке поля (3).Эквипотенциальные поверхности – это поверхности равного потенциала.
32. Связь между потенциалом поля тяготения и его напряженностью. Элементраная работа при перемещ точки определ dA=(-γ*m*M/R²)dR; φ=-γ*M/R;dA=-mdφ;dA=F*dl=m* g*dl;m*g*dl=-m*dφ; g=-dφ/dl – характеристика из менения потенциала на единицу длины в направ лении перемещения поля тяготения.g=-grad(φ) (где g-вектор); grad=(∂φ/∂x)*i+(∂φ/∂y)*j+(∂φ/∂x)*k (где i,j,k-векторы);Знак «-» указывает, что вектор напряжен ности g направлен в сторону убывания потенциала φ (φ-вектор).Первая космическая скорость – это минимальная скорость, которую надо сообщить тело, чтобы оно могло двигаться вокруг Земли по круговой орбите.γ*m*M/R²=m*υ²/R, R-радиус Земли; υ1=√γ*(M/R²)*R=√g*R=7,9 км/c;Вторая космическая скорость – это минимальная скорость, которую надо сообщить телу, чтобы оно могло преодолеть притяжение Земли и превратиться в спутник Солн ца.m*υ²/2=∫|R-8|(γ*m*M/R²)dR=γ*m*M/R;υ2=√2*g*R= 11,2 км/с;Третья космическая скорость – это ско рость, которую необходимо сообщить телу на Зем ле, чтобы оно преодолело притяжение Солнца. υ3=16,7 км/с.
Силы инерции. m*ā1=m*ā+Fин, Fин - сила инерции, вектор. Силы инерции при этом должны быть такими, чтобы вместе с силами F, обусловленными воздействием тел друг на друга, они сообщали телу ускорение a1, каким оно обладает в неинерциальных систем ах отсчета. F=m*a, a – ускорение тела в инерциаль ных системах отсчета.Силы инерции – силы, обусл овленные ускоренным движением системы отсче та относительно измеряемой системы отсчета. Си лы инерции вызываются не взаимодействием движу щихся тел, а ускоренным движением системы отс чета, поэтому они не подчиняются 3 закону Ньюто на.Проявления сил инерции:1. Силы инерции, воз никающие при ускоренном поступательном дви жении системы отсчета.Fин=-m*ā;Они проявляются в перегрузках при запуске космического корабля.
34. Давление жидкости. З-н Паскаля, Архимеда. Несжимаемая жидкость. Гидростатическое давление. Давление жидкости – физическая величина, опре деляемая нормальной силой, действующей со сто роны жидкости на единицу площади.P=∆F/∆SЗакон Паскаля:Давление в любом месте покоящейся жид кости одинаково по всем направлениям, причем давление одинаково передается по всему объему. Закон Архимеда:На тело, погруженное в жидкость (газ) действует со стороны этой жидкости (газа) вы талкивающая сила, направленная вверх и равная весу вытесненной телом жидкости. Fa=ρgVНесжи маемая жидкость – это жидкость, зависимость плотности которой от давления в данной задаче можно пренебречь.Гидростатическое давление. Если жидкость несжимаема, тогда при попереч ном сечении S столба жидкости, его высоте h, пло тности ρ вес равен p=ρgSh, а давление на нижнее основание P=p/S=ρgh.
35. Ур-е неразрывности. Течение – движение жидкости.Поток – совокупность частиц, движущейся жидкости. Лиyии тока – линия, в каждой точке которой каса тельная к ней совпадает по направлению с вектор ом скорости в данный момент времени (использу ются для графического изображения жидкости). Линии тока проводятся так, чтобы густота их была больше там, где больше скорость движения жидк ости.Трубка тока – часть жидкости, ограниченная линиями.Стационарное течение это течение жид кости, при котором форма и расположение линии тока, а также знак скоростей в каждой точке не ме няется со временем.Ур-е неразрывности для нес жимаемой жидкости:Рассмотрим трубку тока, выб рав два сечения S1, S2 перпендикулярные направле нию скоростей. За время ∆t через сечение S проходит объем жидкости V=ρυ∆t. Если жидкость несжимаема, то через площадь S1 за единицу времени пройдет такой же объем жидкости, как и через S2, тогда S1*υ1=S2*υ2 или S*υ=const – уравнение неразрывности.
Ур-е Бернулли. Ур-е Бернулли: В стационарно-текущей идеальной жидкости (отсутствует сила внутреннего трения) выбираем трубку тока, ограниченную сечениями S1, S2. По закону сохранения энергии: изменение полной энергии жидкости массой m в местах сечений S1, S2 равно работе внешних сил по перемещению этой массы жидкости, т.е. E2-E1=A, где E1=m*υ1²/2 +m*g*h1, E2= m*υ2²/2 +m*g*h2;A=F1*L1+F2*L2, где F – внешние си лы, F1=P1*S1, L1=υ1*∆t; Согласно ур-ю неразрыв ности для несжимаемой жидкости: ∆V=S1*υ1*∆t= S2*υ2*∆t;ρ*υ1²/2+ρ*g*h1+P1= ρ*υ2²/2+ρ*g*h2+P2, где ρ – плотность жидкости.ρ*υ²/2+ρ*g*h+P=const – Ур-е Бернулли, где P – статическое давление.
Применение ур Бернулли.
Монометры: Из ур-я Бернулли для горизонтальной трубки тока можно записать ρ*υ²/2+P=const и уравнение неразрывности S*υ=const => что при течении жидкости по гори зонтальной трубе имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление бол-е в более шир-х местах. Скорость истечения жидкости через малое отверстие в стенке сосуда: Ур-е Бернулли для двух сечений, одно из которых на уровне h1 свободной поверхности жидкости, h2 – свободное отверстие из сосуда. ρ*υ1²/2+ρ*g*h1+P1= ρ*υ2²/2+ρ*g*h2+P2; υ1²/2+ g*h1 = υ2²/2+ g*h2;S1*υ1=S2*υ2; S1>>S2; υ2²=2*g*(h1-h2)=2*g*h; υ=√2*g*h – ф-ла Ториччели. Скорость υ2 совпадает со скоростью, которую приобретает тело падая с высоты h, этот результат справедлив для идеальной жидкости.
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.166.45 (0.007 с.) |

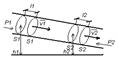
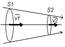 2. Силы инерции, действующие на тело, которое покоится во вращающейся системе отсчета.Fц=-m*ω²*R, Fц – центробежная сила инерции.Их дейс твию подвергаются пассажиры в движущемся тра нспорте на повороте.3. Силы инерции, действующ ие на тела движущиеся во вращающейся системе отсчета.Fк=2*m*[υ²×ω] – кориолисова сила инерции, где Fк,υ,ω – векторы.Кориолисова сила перпенди кулярна скорости тела и угловой скорости систе мы отсчета в соответствии с правилом правого винта.m*ā’=F+Fин+Fц+Fк, где F,Fин,Fц,Fк – векторы.
2. Силы инерции, действующие на тело, которое покоится во вращающейся системе отсчета.Fц=-m*ω²*R, Fц – центробежная сила инерции.Их дейс твию подвергаются пассажиры в движущемся тра нспорте на повороте.3. Силы инерции, действующ ие на тела движущиеся во вращающейся системе отсчета.Fк=2*m*[υ²×ω] – кориолисова сила инерции, где Fк,υ,ω – векторы.Кориолисова сила перпенди кулярна скорости тела и угловой скорости систе мы отсчета в соответствии с правилом правого винта.m*ā’=F+Fин+Fц+Fк, где F,Fин,Fц,Fк – векторы.