
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аксиомы статики твердого телаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В основе статики твердого тела лежат аксиомы, установленные из опытов и наблюдений. Всё содержание статики может быть получено дедуктивно (т.е. посредством логических умозаключений с использованием соответствующего математического аппарата) как следствие этих аксиом. Аксиома 1 (о равновесии двух сил). Две силы, приложенные к абсолютно твердому телу, уравновешиваются тогда и только тогда, когда они равны по величине, противонаправлены и имеют общую линию действия (рис. 1.4). Аксиома 2 (о присоединении и исключении уравновешенных сил). Действие данной системы сил на твердое тело не изменяется, если к ней присоединить или исключить из нее уравновешенную систему. Из аксиом 1 и 2 логически получаем следствие: не изменяя действия силы на твердое тело, можно переносить точку приложения силы вдоль линии действия. Иногда этот факт выражают словами: сила, приложенная к абсолютно твердому телу, есть вектор скользящий. В самом деле (рис. 1.5), При формулировании этой аксиомы полагают, что сила при переносе точки ее приложения работы не совершает.
Величину равнодействующей силы можно определить по теореме косинусов
или по теореме синусов
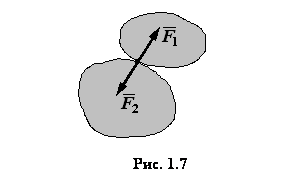
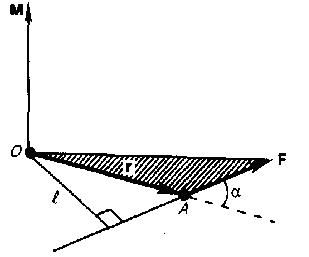
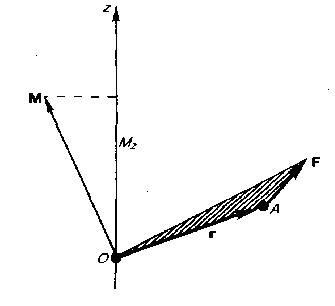
Аксиома 4 (о действии и противодействии). Два тела действуют друг на друга с силами, равными по величине и направленными по одной прямой в противоположные стороны (рис. 1.7). Заметим, что эти силы приложены к разным телам. Аксиома 5 (аксиома отвердевания). Равновесие нетвердого тела не нарушится, если при тех же действующих на него силах оно затвердеет и станет абсолютно твердым. На основании этой аксиомы результаты, полученные в статике абсолютно твердого тела, можно применять к деформируемым телам. Утверждение, обратное аксиоме 5, неверно (если тело перестает быть твердым, то его равновесие может нарушиться). Аксиома 6 (аксиома освобождаемости от связей). Не изменяя состояния несвободного тела, можно отбросить наложенные на него связи, приложив их реакции, после чего рассматривать тело как свободное. Момент силы Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F (рис. 1):
Рис.1
Здесь М - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы
где α - угол между r и F; rsinα= l - наименьшее расстояние между линией действия силы и точкой О - плечо силы. Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис. 2).
Рис.2
Значение момента Мz не зависит от выбора положения точки О на оси z.
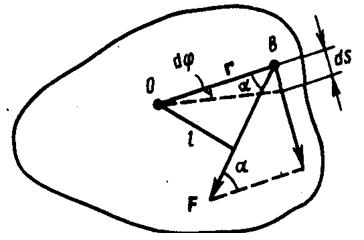
Найдем выражение для работы при вращении тела (рис.3).
Рис.3
Пусть сила F приложена в точке В, находящейся от оси z на расстоянии r, α - угол между радиусом-вектором r и направлением силы. Так как тело абсолютно твердое, то работа этой силы равна работе, которую необходимо затратить на поворот всего тела. При повороте тела на бесконечно малый угол dφ точка приложения В проходит путь ds=rdφ и работа равна произведению проекции силы на направление с мещения на величину смещения:
Учитывая (1), можем записать
где Frsinα=F l =Mz - момент силы относительно оси z. Значит, работа при вращении тела равна произведению момента действующей силы на угол поворота.
Уравнение (3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
где J - главный момент инерции тела (момент инерции относительно главной оси). БИЛЕТ Момент инерции: Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м². Теорема Штейнера Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
Кинетическая энергия тела, вращающегося вокруг неподвижной оси:
Момент силы, действующей в плоскости, перпендикулярной оси вращения
Момент импульса твердого тела
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1040; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.37.40 (0.009 с.) |


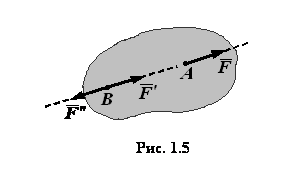 пусть на твердое тело действует сила
пусть на твердое тело действует сила 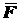 , приложенная в точке
, приложенная в точке 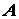 . Приложим в произвольной точке
. Приложим в произвольной точке 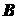 , лежащей на линии действия силы
, лежащей на линии действия силы 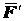 и
и 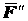 , причем
, причем 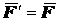 ,
, 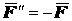 . Согласно аксиоме 2 полученная система из трех сил эквивалентна силе
. Согласно аксиоме 2 полученная система из трех сил эквивалентна силе 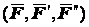 , а потому и данной силе
, а потому и данной силе 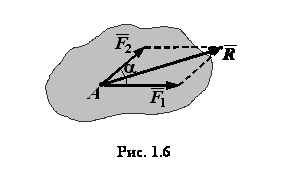 Аксиома 3 (закон параллелограмма). Равнодействующая двух сил, приложенных к одной точке тела под углом друг к другу, выражается по величине и по направлению диагональю параллелограмма, построенного на заданных силах (рис.1.6):
Аксиома 3 (закон параллелограмма). Равнодействующая двух сил, приложенных к одной точке тела под углом друг к другу, выражается по величине и по направлению диагональю параллелограмма, построенного на заданных силах (рис.1.6):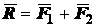 .
.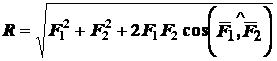
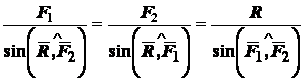 .
.
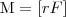
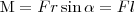 (1)
(1)
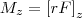
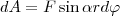 (2)
(2)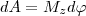
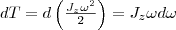 поэтому
поэтому 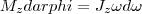 , или
, или 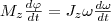
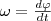 получаем
получаем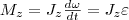 (3)
(3)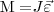
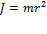
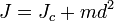 ,
,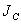 - момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси;
- момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси; - расстояние между осями;
- расстояние между осями;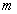 - масса тела.
- масса тела.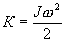 , где
, где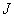 - момент инерции;
- момент инерции;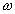 - угловая скорость.
- угловая скорость.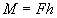 , где
, где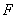 - сила,
- сила,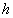 - плечо силы (кратчайшее расстояние от оси вращения до линии действия силы).
- плечо силы (кратчайшее расстояние от оси вращения до линии действия силы).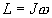 .
.


