
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения динамики вращательного движения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку
Основной закон динамики вращательного движения – аналог второго закона Ньютона для поступательного движения.
БИЛЕТ Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях). Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр. Момент импульса замкнутой системы сохраняется. Закон сохранения момента импульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем. Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
БИЛЕТ Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением. Основные кинематические характеристики вращательного движения тела — его угловая скорость (
и кинетическая энергия
где Iz — момент инерции тела относительно оси вращения. Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I1, I2 и I3. Вращательная энергия такой молекулы задана выражением
где ω1, ω2, и ω3 — главные компоненты угловой скорости. В общем случае, энергия при вращении с угловой скоростью
БИЛЕТ Степени свободы. Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы. Примеры
Степени свободы молекулы: Формула внутренней энергии газа:
и прямо связанная с ней формула для средней энергии молекулы газа
где
— включают количество степеней свободы молекулы. Степени свободы молекулы вымораживаются, как это описано в параграфе выше, что означает, что эффективное i в формуле зависит от температуры и, вообще говоря, не может быть просто вычислено классическим механическим способом. Все вращательные степени свободы у одноатомных молекул и вращательная степень свободы, соответствующая вращению вокруг продольной оси у линейных (в реальном геометрическом смысле) молекул, выморожены (то есть не должны учитываться в i) всегда, поскольку их температуры вымораживания настолько высоки, что диссоциация молекул происходит гораздо раньше, чем эти температуры достигаются.
МОЛЕКУЛЯРНАЯ
Вопрос Молекулярно-кинетическая теория (сокращённо МКТ) — теория XIX века, рассматривавшая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:
Основными доказательствами этих положений считались:
В современной (теоретической) физике термин молекулярно-кинетическая теория уже не используется, хотя он встречается в учебниках по курсу общей физики. В современной физике МКТ заменила кинетическая теория, в русскоязычной литературе — физическая кинетика, и статистическая механика. В этих разделах физики изучаются не только молекулярные (атомные или ионные) системы, находящиеся не только в «тепловом» движении, и взаимодействующие не только через абсолютно упругие столкновения. Абсолютная температура. Понятие абсолютной температуры было введено У. Томсоном (Кельвином), в связи с чем шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры — кельвин (К). Абсолютная шкала температуры называется так, потому что мера основного состояния нижнего предела температуры — абсолютный ноль, то есть наиболее низкая возможная температура, при которой в принципе невозможно извлечь из вещества тепловую энергию. Абсолютный ноль определён как 0 K, что равно −273.15 °C. Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона. Законы Дальтона Законы Дальтона — два физических закона, определяющих суммарное давление и растворимость смеси газов. Сформулированы Джоном Дальтоном в начале XIX века
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 605; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.49.23 (0.009 с.) |




 ) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:
) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:


 находится по формуле:
находится по формуле: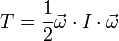 , где
, где  — тензор инерции.
— тензор инерции. ,
, ,
, — количество степеней свободы молекулы газа,
— количество степеней свободы молекулы газа, — количество газа (
— количество газа ( — масса,
— масса,  — молярная масса газа),
— молярная масса газа), — универсальная газовая постоянная,
— универсальная газовая постоянная,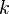 — константа Больцмана,
— константа Больцмана, — абсолютная температура газа,
— абсолютная температура газа,
 — давление,
— давление, — универсальная газовая постоянная
— универсальная газовая постоянная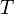 — абсолютная температура,К.
— абсолютная температура,К.


