Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа. Исследование законов вращательного движенияСодержание книги
Поиск на нашем сайте
Цель работы: изучение законов динамики вращательного движения и их экспериментальная проверка.
Основные понятия и закономерности
Вращательным движением тела называется такое движение, при котором все точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. При вращательном движении тела изменение его кинематических и динамических характеристик зависит от вращающего момента, действующего на тело, и момента инерции тела. Основными кинематическими характеристиками вращательного движения являются угловая скорость ω и угловое ускорение ε:
где φ – угловое перемещение тела или угол поворота. Связь между линейной υ и угловой ω скоростями вращающегося тела и линейным аτ и угловым ε ускорениями можно установить, если выразить длину дуги окружности, по которой происходит вращение, через угол поворота φ: S= φ·r
Тогда:
где r – расстояние от точки до оси вращения (модуль радиуса – вектора точки). Угловая скорость ω и угловое ускорение ε – векторные величины. Вектор Направление вектора При вращательном движении тела изменение его кинематических и динамических характеристик от момента инерции тела и действующего на тело вращающего момента.
Вращающим моментом или моментом вращающей силы называется векторная величина
где Модуль момента силы равен
где r sinα = l – плечо силы F (рисунок 2.2,б) l =OC= r sinα – кратчайшее расстояние от оси вращения до прямой, вдоль которой действует сила Твердое тело представляет собой совокупность материальных точек массой mi. Момент сил, действующих на материальную точку, равен
где
Момент сил, действующих на материальные точки:
По второму закону Ньютона
следовательно,
где Соотношение (2.7) можно записать в виде:
где Поэтому момент внешних сил, действующих на тело, – вращающий момент
Следовательно, учитывая соотношения (2.9) и (2.11), имеем
где
Момент внешних сил, действующих на тело, равен произведению момента инерции тела на угловое ускорение
Полученное соотношение (2.13) – основной закон динамики вращательного движения. Из закона динамики вращательного движения следует, что момент силы Для тела плотностью ρ момент инерции вычисляется суммированием моментов инерции всех его материальных точек:
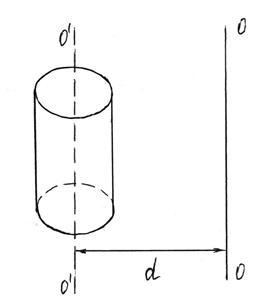
где Момент инерции является физической величиной, характеризующей инертность тела при вращательном движении под действием вращающего момента (аналогично массе тела при поступательном движении, но m = const). Момент инерции тела зависит от формы тела, его размеров и расположения тела относительно оси вращения. Момент инерции тела относительно произвольной оси вращения определяется по теореме Штейнера. Момент инерции тела I относительно произвольной оси вращения ОО равен сумме момента инерции тела I0 относительно оси О/О/, проходящей через центр массы тела параллельно оси ОО, и произведения массы тела m на квадрат расстояния d между параллельными осями (рисунок 2.4).
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.011 с.) |

 ,
, 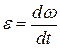 или
или  , (2.1)
, (2.1)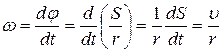 ;
; 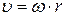 , (2.2)
, (2.2) ;
; 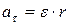 , (2.3)
, (2.3) направлен по оси вращения так, что из его конца вращение видно происходящим против часовой стрелки (правый винт, рисунок 2.1,а).
направлен по оси вращения так, что из его конца вращение видно происходящим против часовой стрелки (правый винт, рисунок 2.1,а). совпадает с направлением вектора
совпадает с направлением вектора  , если
, если 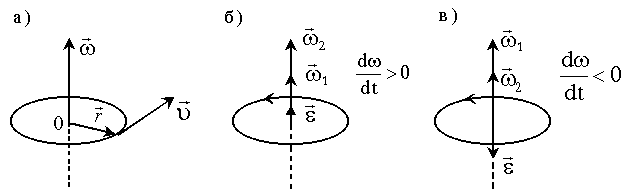
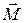 , равная векторному произведению радиуса-вектора
, равная векторному произведению радиуса-вектора  (проводится от центра вращения точки О в точку приложения силы, точку А) на вектор силы
(проводится от центра вращения точки О в точку приложения силы, точку А) на вектор силы  (рисунок 2.2)
(рисунок 2.2)
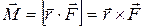 , (2.4)
, (2.4)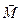 – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от
– псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 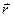 к
к  (рисунок 2.2). Векторы
(рисунок 2.2). Векторы 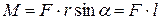 , (2.5)
, (2.5)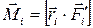 , (2.6)
, (2.6)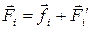 – сумма внутренних
– сумма внутренних 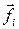 и внешних
и внешних 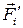 сил, действующих на отдельную точку i (рисунок 2.3).
сил, действующих на отдельную точку i (рисунок 2.3).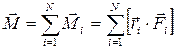 (2.7)
(2.7)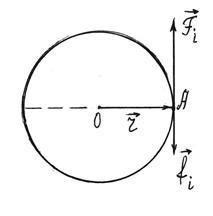
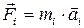 , где
, где  – линейное ускорение материальной точки, связанное с угловым ускорением
– линейное ускорение материальной точки, связанное с угловым ускорением  , (2.8)
, (2.8)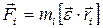 , а момент силы
, а момент силы  равен
равен , (2.9)
, (2.9)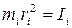 – момент инерции материальной точки равен произведению массы точки mi на квадрат расстояния ri от оси вращения в точке О до точки А.
– момент инерции материальной точки равен произведению массы точки mi на квадрат расстояния ri от оси вращения в точке О до точки А.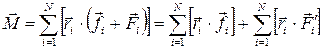 , (2.10)
, (2.10)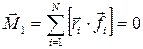 – вращающий момент внутренних сил равен нулю (по третьему закону Ньютона).
– вращающий момент внутренних сил равен нулю (по третьему закону Ньютона). , (2.11)
, (2.11)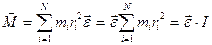 , (2.12)
, (2.12) – момент инерции твердого тела относительно данной оси вращения.
– момент инерции твердого тела относительно данной оси вращения.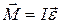 . (2.13)
. (2.13)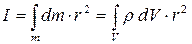 , (2.14)
, (2.14) – бесконечно малая масса тела.
– бесконечно малая масса тела.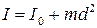 (2.15)
(2.15)