
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика работы и описание установкиСодержание книги
Поиск на нашем сайте
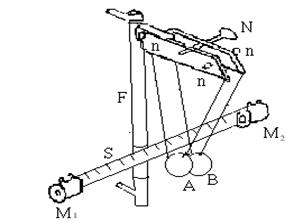
Установка состоит из двух шаров А и B на бифилярных подвесах, укрепленных на кронштейне F (рисунок 4.1) Длину нитей можно изменять с помощью винтов и тем самым осуществлять центровку шаров. Установка снабжена шкалой S для измерения углов отклонения шаров и магнитами М1 и М2, при помощи которых шары удерживаются в отклоненном положении. Если шар отклонить от положения равновесия, он приобретет скорость V. Ее можно найти, использовав закон сохранения энергии.
Рисунок 4.1
В отклоненном положении (рисунок 4.2) шар обладает запасом потенциальной энергии Wп = mgh.
Высоту h можно определить из треугольника ОАС: ОС = l – h = l cos a, откуда h = l (1 – cos a) = 2 l sin2 При прохождении положения равновесия шар обладает кинетической энергией
где I – момент инерции шара, w – его угловая скорость в момент прохождения положения равновесия. Если радиус шара R значительно меньше длины нити l, то шар можно считать материальной точкой, момент инерции которой равен I = ml2, а угловая скорость Подставив I и w в формулу кинетической энергии, получим:
По закону сохранения энергии:
откуда
Подставив в (4.21) h (4.16), получим:
Для определения отношения масс шаров воспользуемся законом сохранения импульса, если один из шаров неподвижен (например, второй шар): m 1 V 1 = m 1 U 1_+ m 2 U 2, (4.23) где m1V1 – импульс первого шара до удара, m1U1 – импульс первого шара после удара, m2U2 – импульс второго шара после удара.
Из формулы (4.23) имеем:
или, учитывая соотношение (4.22), получим:
где aо – угол отклонения первого шара до удара, a1 – угол отклонения первого шара после удара, j – угол отклонения второго шара после удара. При определении коэффициента восстановления шаров их отклоняют перед ударом на одинаковый угол aо. Если шары имеют равные массы, то скорости до и после удара будут равными, т.е. V1 = V2 =V и U1 = U2 = U. Поэтому для коэффициента восстановления шаров будет иметь:
Откуда: U = КV. Следовательно, можно записать систему уравнений: После первого удара: U 1 = КV. После второго удара: U 2 = КU 1. и.т.д. После n- го удара: U n = КU n-1. Перемножив равенства и произведя сокращения, получим:
где V – скорость любого из шаров до удара, Un – скорость этого же шара после n –го удара. Подставив в (4.27) V и Un с учетом (4.22), получим:
где aо – угол отклонения шара до удара, an – угол отклонения шара после n –го удара.
Порядок выполнения работы
4.3.1 Определение отношения масс соударяющихся шаров
1. Проверить центровку шаров. Установить шары в положение равновесия и заметить положение нитей обоих шаров на шкале, т.е. те точки, в которых плоскости нитей пересекают шкалу. 2. Шар А вывести из положения равновесия, закрепив с помощью магнита или рукой, и отметить по шкале угол отклонения 3. Выключить магнит (или отпустить шар) и заметить углы отклонения шара В – φ и шара А – α1 после удара. Повторить измерения не менее трех раз при разных углах 4. Произвести такие же измерения, вначале отклоняя шар В на угол 5. По формуле (4.25) найти отношение масс шаров. 6. Вывести формулы относительной и абсолютной погрешности и вычислить их. 7. Результаты опытов занести в таблицу 4.1.
Таблица 4.1
4.3.2 Определение коэффициента восстановления шаров
1. Установить шары в положение равновесия и заметить положение нитей по шкале. 2. Отклонить оба шара на одинаковые углы 3. Отпустив (отключив магниты) шары, привести их в соударение. Измерить угол отклонения одного из шаров после n – го удара – αn. 4. Опыт повторить не менее трех раз, изменяя угол отклонения 5. По формуле (4.28) рассчитать коэффициент восстановления К. 6. Определить среднее значение < К >, абсолютную и относительную погрешности: <ΔК>, < ΔК>/<К>. 7. Результаты занести в таблицу 4.2.
Таблица 4.2
4.3.3 Определение скорости шаров после неупругого удара
1. Установить шары в положение равновесия и заметить положение нитей по шкале. 2. На один из шаров укрепить небольшой кусочек пластилина такой массы, чтобы масса шара почти не изменилась. 3. Отвести один из шаров от положения равновесия на угол α0. 4. Отпустить шар и заметить угол отклонения шаров α1 после удара. 5. Повторить опыт не менее трех раз при одном значении угла α0 .6. По формуле где l – длина нитей. 7. Определить среднее значение <U> и вычислить абсолютную и относительную погрешности. 8. Вычислить скорость шаров после удара по формуле (4.22) и сравнить со скоростью, полученной в пункте 6.
4.4 Контрольные вопросы
1. Сформулировать и записать закон сохранения импульса. 2. Сформулировать и записать закон сохранения энергии в механике. 3. Вывести формулу скоростей шаров после упругого и неупругого ударов. 4. Вывести рабочие формулы для отношения масс шаров, скорости шаров перед и после удара, коэффициент восстановления шаров. 5. Каков физический смысл коэффициента восстановления шаров К? 6. Вывести формулу для вычисления погрешностей.
Техника безопасности
1. Перед выполнением работы проверить прочность закрепления всех частей установки. 2. Не включать электрическую схему без проверки преподавателем или лаборантом.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.009 с.) |


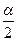 . (4.16)
. (4.16)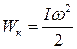 , (4.17)
, (4.17) .
.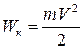 . (4.19)
. (4.19)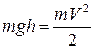 , (4.20)
, (4.20) . (4.21)
. (4.21) . (4.22)
. (4.22)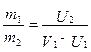 (4.24)
(4.24)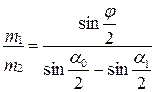 , (4.25)
, (4.25)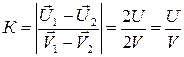 . (4.26)
. (4.26)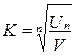 , (4.27)
, (4.27)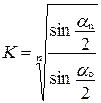 , (4.28)
, (4.28)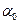 (в градусах) – рисунок 4.1.
(в градусах) – рисунок 4.1.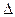 К
К
 вычислить скорость шаров после неупругого удара, учитывая, что
вычислить скорость шаров после неупругого удара, учитывая, что 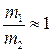 и
и 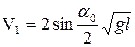 ,
,


