
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Погрешность косвенных измеренийСодержание книги
Поиск на нашем сайте
Многие физические величины сложно или невозможно измерить прямыми методами. Например, сложно с помощью мер длины измерить размеры атома или расстояние от Земли до Марса. Поэтому прибегают к косвенным измерениям. Косвенное измерение – измерение, при котором искомое значение физической величины получают вычислением на основании зависимости ее от величин, измеряемых прямыми методами. Например, скорость тела можно определить, если измерить S – расстояние, пройденное телом и t – время, за которое этот путь пройден:
В данном случае необходимо прямым методом измерить длину маятника – Погрешность косвенно измеряемой величины зависит от погрешностей входящих в нее непосредственно (прямо) измеряемых величин и табличных значений, от вида расчетной формулы. В наиболее часто встречающихся случаях пользуются формулами для вычисления абсолютных и относительных погрешностей. Если расчетная формула имеет сложный вид, то следует вывести формулу для вычисления погрешности, исходя из рабочей формулы. Если формула удобна для логарифмирования, то сначала вычисляют относительную погрешность. Для вывода формулы относительной погрешности используют метод логарифмическогодифференцирования. Рассмотрим этот метод на примере. Пусть косвенно измеряемая величина X вычисляется по формуле:
где p, a, b, c, k – величины, измеряемые прямо, либо табличные величины. 1. Выражение следует прологарифмировать.
2. Полученное выражение следует продифференцировать, считая табличные величины и величины измеряемые прямо переменными.
3. Заменить дифференциалы величин на их приращения. 4. Для того, чтобы получить выражение относительной погрешности
Для расчета в полученную формулу необходимо подставить значения абсолютных погрешностей прямо измеренных и табличных величин (Dp, D a, D b, D c, D k). В случае многократных измерений для вычисления
Существует еще один способ вывода формулы для вычисления погрешности. Пусть функция f является функцией одной переменной x, тогда d f = f ¢х × dх. Если f является функцией нескольких переменных f (x, y, z,...), то
df = f ¢х × dх + f ¢y × dy + f ¢z × dz + … (1.15)
где f ¢х, f ¢y, f ¢z – частные производные функции f соответственно по x, y, z,... Если в формуле 1.15 дифференциалы заменить приращениями и учесть, то, что погрешности только складываются, получим формулу абсолютной погрешности:
D f = f ¢х × Dх + f ¢y × Dy + f ¢z × Dz + … (1.16)
Относительная погрешность Следовательно:
Для примера рассмотрим функцию X, заданную формулой 1.12
Находим полный дифференциал функции X, считая переменными все входящие в нее величины, включая p:
Заменяем “ d ” на “D” и (–) на (+), получаем:
Разделив (1.18) на выражение для X (1.12), получим:
Формула (1.19) совпадает с формулой (1.13). Сравнивая формулы (1.18) и (1.19), видим, что формула для вычисления относительной погрешности значительно проще. В большинстве случаев и считают сначала относительную погрешность, а потом абсолютную: D X = e × X.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 480; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.009 с.) |

 . Ускорение свободного радения можно определить из соотношения для периода математического маятника:
. Ускорение свободного радения можно определить из соотношения для периода математического маятника: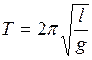 . (1.11)
. (1.11) , Т– период, длительность одного полного колебания, и воспользоваться табличной величиной – p. Все величины, измеренные прямо, обладают погрешностью, табличные величины тоже имеет погрешность. Следовательно, результат вычислений, основанный на математических операциях с величинами, обладающими погрешностью, также будет характеризоваться какой-то погрешностью. Физическая величина, найденная косвенным способом, характеризуется абсолютной и относительной погрешностью, которые определяются различными способами.
, Т– период, длительность одного полного колебания, и воспользоваться табличной величиной – p. Все величины, измеренные прямо, обладают погрешностью, табличные величины тоже имеет погрешность. Следовательно, результат вычислений, основанный на математических операциях с величинами, обладающими погрешностью, также будет характеризоваться какой-то погрешностью. Физическая величина, найденная косвенным способом, характеризуется абсолютной и относительной погрешностью, которые определяются различными способами. , (1.12)
, (1.12)

 , необходимо взять все относительные погрешности со знаком плюс (заменить знак «–» на «+»).
, необходимо взять все относительные погрешности со знаком плюс (заменить знак «–» на «+»). (1.13)
(1.13) используют средние значения величин. Определив относительную погрешность, можно вычислить абсолютную погрешность косвенно измеряемой величины:
используют средние значения величин. Определив относительную погрешность, можно вычислить абсолютную погрешность косвенно измеряемой величины: (1.14)
(1.14) .
. (1.17)
(1.17) .
.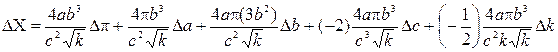 (1.18)
(1.18) (1.19)
(1.19)


