
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные кинематические величиныСодержание книги Поиск на нашем сайте
Перемещение — векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени:
Иными словами, перемещение — это приращение радиус-вектора за выбранный промежуток времени. Мгновенная скорость — векторная физическая величина, равная первой производной от радиус-вектора по времени:
Характеризует быстроту перемещения материальной точки. Мгновенную скорость можно определить как предел средней скорости при устремлении к нулю промежутка времени, на котором она вычисляется:
Мгновенное ускорение — векторная физическая величина, равная второй производной от радиус-вектора по времени и, соответственно, первой производной от мгновенной скорости по времени:
Характеризует быстроту изменения скорости. Единица ускорения в системе СИ— м/с², в системе СГС — см/с². В случае движения в плоскости вектор ускорения можно разложить по сопутствующему базису: на вектор нормального и тангенциального ускорения:
Здесь
В случае движения по окружности нормальное ускорение называется центростремительным. Как видно из предыдущей формулы, при движении по окружности с постоянной скоростью нормальное ускорение постоянно по модулю и направлено к центру окружности. Величина
Путь — Путь м.т. расстояние измеряемое по траектории (линии, описываемой точкой при ее движении) вдоль движения м.т
Графическое представление График скорости (проекции скорости)
Для того чтобы построить этот график, на оси абсцисс откладывают время движения, а на оси ординат - скорость (проекцию скорости) тела. График скорости показывает, как изменяется скорость тела с течением времени. В прямолинейном равномерном движении скорость с течением времени не изменяется. Поэтому график скорости такого движения представляет собой прямую, параллельную оси абсцисс (оси времени). 2. График зависимости координаты тела от времени
Для построения этого графика (который иначе называют графиком движения) на оси абсцисс откладывают время движения, а на оси ординат - координату движущегося тела. 3. График пути
Для выражения зависимости пути, проходимого телом, от времени его движения строят график пути. Для этого на оси абсцисс откладывают время, а на оси ординат - пройденный телом путь. Зависимость пути от времени линейная, следовательно, график этой зависимости является прямой линией Графическое представление 1.
Для построения этого графика на оси абсцисс откладывают время движения, а на оси ординат - скорость (проекцию скорости) тела. В равноускоренном движении скорость тела с течением времени изменяется 2. График зависимости координаты от времени (график движения)
Для построения этого графика на оси абсцисс откладывают время движения, а на оси ординат - координату движущегося тела. 3. График пути
Для того чтобы построить этот график, на оси абсцисс откладывают время, а на оси ординат - длину пути, пройденного телом.
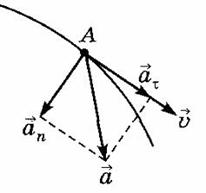
ВОПРОС Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек. Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции vx и vy ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времени t определяется по формулам Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости. При криволинейном движении ускорение можно представить как сумму нормальной v – мгновенное значение скорости, r – радиус кривизна траектории в данной точке. Полное ускорение, с которым движется материальная точка, равно:
Кроме центростремительного ускорения, важнейшими характеристиками равномерного движения по окружности являются период и частота обращения. Период обращения — это время, за которое тело совершается один оборот. Обозначается период буквой Т (с) и определяется по формуле: где t — время обращения, п — число оборотов, совершенных за это время. Частота обращения — это величина, численно равная числу оборотов, совершенных за единицу времени. Обозначается частота греческой буквой Измеряется частота в 1/с. Период и частота — величины взаимно обратные: Если тело, двигаясь по окружности со скоростью v, делает один оборот, то пройденный этим телом путь можно найти, умножив скорость v на время одного оборота: l = vT. С другой стороны, этот путь равен длине окружности 2π r. Поэтому vT = 2π r, где w (с-1) - угловая скорость. При неизменной частоте обращения центростремительное ускорение прямо пропорционально расстоянию от движущейся частицы до центра вращения. Угловая скорость (w) – величина, равная отношению угла поворота радиуса, на котором находится вращающаяся точка, к промежутку времени, за который произошел этот поворот:
Связь между линейной и угловой скоростями: v= wr. Движение тела можно считать известным лишь тогда, когда известно, как движется каждая его точка. Самое простое движение твердых тел – поступательное. Поступательным называется движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается параллельно самой себе. БИЛЕТ Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени Динамика — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия. Силы в природе: Закон всемирного тяготения. Подобно тому как Луна движется вокруг Земли, Земля в свою очередь обращается вокруг Солнца. Вокруг Солнца обращаются Меркурий, Венера, Марс, Юпитер и другие планеты Солнечной системы. Ньютон доказал, что движение планет вокруг Солнца происходит под действием силы притяжения, направленной к Солнцу и убывающей обратно пропорционально квадрату расстояния от него. Земля притягивает Луну, а Солнце — Землю, Солнце притягивает Юпитер, а Юпитер — свои спутники и т. д. Отсюда Ньютон сделал вывод, что все тела во Вселенной взаимно притягивают друг друга. Силу взаимного притяжения, действующую между Солнцем, планетами, кометами, звездами и другими телами во Вселенной, Ньютон назвал силой всемирного тяготения. Сила всемирного тяготения, действующая на Луну со стороны Земли, пропорциональна массе Луны (см. формулу 9.1). Очевидно, что сила всемирного тяготения, действующая со стороны Луны на Землю, пропорциональна массе Земли. Эти силы по третьему закону Ньютона равны между собой. Следовательно, сила всемирного тяготения, действующая между Луной и Землей, пропорциональна массе Земли и массе Луны, т. е. пропорциональна произведению их масс. Распространив установленные закономерности — зависимость силы тяжести от расстояния и от масс взаимодействующих тел — на взаимодействие всех тел во Вселенной, Ньютон открыл в 1682 г. закон всемирного тяготения: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними:
Векторы сил всемирного тяготения направлены вдоль прямой, соединяющей тела. Закон всемирного тяготения в такой форме может быть использован для вычисления сил взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними. Ньютон доказал, что для однородных шарообразных тел закон всемирного тяготения в данной форме применим при любых расстояниях между телами. За расстояние R между телами в этом случае принимается расстояние между центрами шаров. Силы всемирного тяготения называют гравитационными силами, а коэффициент пропорциональности G в законе всемирного тяготения называют гравитационной постоянной. Вес и невесомость Вес тела. В технике и быту широко используется понятие веса тела. Весом тела называют силу, с которой тело вследствие его притяжения к Земле действует на горизонтальную опору или подвес. Вес тела
Если тело находится в покое на горизонтальной поверхности или равномерно движется и на него действуют только сила тяжести
Сопоставив выражения (10.1) и (10.2), получим
т. е. вес При ускоренном движении тела и опоры вес По второму закону Ньютона при движении тела массой
Из уравнений (10.1) и (10.4) для веса
или
Рассмотрим случай движения лифта, когда ускорение
Так как проекции положительны и параллельны координатной оси, их можно заменить модулями векторов:
Вес тела, направление ускорения которого совпадает с направлением ускорения свободного падения, меньше веса покоящегося тела. Невесомость. Если тело вместе с опорой свободно падает, то a = g, и из формулы (10.7) следует, что P = 0. Исчезновение веса при движении опоры с ускорением свободного падения называется невесомостью. Состояние невесомости наблюдается в самолете или космическом корабле при движении с ускорением свободного падения независимо от направления и значения модуля скорости их движения. За пределами земной атмосферы при выключении реактивных двигателей на космический корабль действует только сила всемирного тяготения. Под действием этой силы космический корабль и все тела, находящиеся в нем, движутся с одинаковым ускорением; поэтому в корабле наблюдается явление невесомости. Сила упругости. Закон Гука. При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости. Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше. Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах.
Упругую силу N действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба. В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала
Сила трения. Сила трения покоя не может превышать некоторого максимального значения (Fтр)max. Если внешняя сила больше (Fтр)max, возникает относительное проскальзывание. Силу трения в этом случае называют силой трения скольжения. Она всегда направлена в сторону, противоположную направлению движения и, вообще говоря, зависит от относительной скорости тел. Однако, во многих случаях приближенно силу трения скольжения можно считать независящей от величины относительной скорости тел и равной максимальной силе трения покоя. Эта модель силы сухого трения применяется при решении многих простых физических задач Опыт показывает, что сила трения скольжения пропорциональна силе нормального давления тела на опору, а следовательно, и силе реакции опоры
Коэффициент пропорциональности μ называют коэффициентом трения скольжения. Коэффициент трения μ – величина безразмерная. Обычно коэффициент трения меньше единицы. Он зависит от материалов соприкасающихся тел и от качества обработки поверхностей. При скольжении сила трения направлена по касательной к соприкасающимся поверхностям в сторону, противоположную относительной скорости N– сила реакции опоры, P= - N – вес тела, При движении твердого тела в жидкости или газе возникает силa вязкого трения. Сила вязкого трения значительно меньше силы сухого трения. Она также направлена в сторону, противоположную относительной скорости тела. При вязком трении нет трения покоя. Сила вязкого трения сильно зависит от скорости тела. При достаточно малых скоростях Fтр ~ υ, при больших скоростях Fтр ~ υ2. При этом коэффициенты пропорциональности в этих соотношениях зависят от формы тела. Силы трения возникают и при качении тела. Однако силы трения качения обычно достаточно малы. При решении простых задач этими силами пренебрегают. Законы Ньютона. Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела. Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО). В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
где Или в более известном виде:
Третий закон Ньютона. Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.
БИЛЕТ Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы.
Энергия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется во времени. Это утверждение носит название закона сохранения энергии Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением. Потенциальная энергия Единицей измерения энергии в СИ является Джоуль. Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии. Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.
БИЛЕТ Импульс силы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени (в поступательном движении).
Импульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:
Закон сохранения импульса (Закон сохранения количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. Как и любой из фундаментальных законов сохранения, закон сохранения импульса описывает одну из фундаментальных симметрий, — однородность пространства.
БИЛЕТ Закон сохранения импульса лежит в основе реактивного движения. Реактивное движение — это такое движение тела, которое возникает после отделения от тела его части. Закон сохранения энергии Сумма кинетической и потенциальной энергий тел называется полной механической энергией. Поэтому закон сохранения энергии можно сформулировать так: полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения и упругости, остается постоянной. Основное содержание закона сохранения энергии заключается не только в установлении факта сохранения полной механической энергии, но и в установлении возможности взаимных превращений кинетической и потенциальной энергий в равной количественной мере при взаимодействии тел. Закон сохранения полной механической энергии в процессах с участием сил упругости и гравитационных сил является одним из основных законов механики. Знание этого закона упрощает решение многих задач, имеющих большое значение в практической жизни. Например, для получения электроэнергии широко используется энергия рек. С этой целью строят плотины, перегораживают реки. Под действием сил тяжести вода из водохранилища за плотиной движется вниз по колодцу ускоренно и приобретает некоторую кинетическую энергию. При столкновении быстро движущегося потока воды с лопатками гидравлической турбины происходит преобразование кинетической энергии поступательного движения воды в кинетическую энергию вращательного движения роторов турбины, а затем с помощью электрического генератора — в электрическую энергию. Механическая энергия не сохраняется, если между телами действуют силы трения. Автомобиль, двигавшийся по горизонтальному участку дороги после выключения двигателя, проходит некоторый путь и под действием сил трения останавливается. Во время торможения автомобиля произошло нагревание тормозных колодок, шин автомобиля и асфальта. В результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул. Таким образом, при любых физических взаимодействиях энергия не возникает, а только превращается из одной формы в другую. Этот экспериментально установленный факт называется законом сохранения и превращения энергии. Источники энергии на земле велики и разнообразны. Когда-то в древности люди знали только один источник энергии — мускульную силу и силу домашних животных. Энергия возобновлялась за счет пищи. Теперь большую часть работы делают машины, источником энергии для них служат различные виды ископаемого топлива: каменный уголь, торф, нефть, а также энергия воды и ветра. Если проследить «родословную» всех этих разнообразных видов энергии, то окажется, что все они являются энергией солнечных лучей. Энергия окружающего нас космического пространства аккумулируется Солнцем в виде энергии атомных ядер, химических элементов, электромагнитных и гравитационных полей. Солнце, в свою очередь, обеспечивает Землю энергией, проявляющейся в виде энергии ветра и волн, приливов и отливов, в форме геомагнетизма, различного вида излучений (в том числе и радиоактивности недр и т.д.), мускульной энергии животного мира. Геофизическая энергия высвобождается в виде природных стихийных явлений (вулканизм, землетрясения, грозы, цунами и т.д.), обмена веществ в живых организмах (составляющих основу жизни), полезной работы по перемещению тел, изменению их структуры, качества, передачи информации, запасания энергии в различного рода аккумуляторах, конденсаторах, в упругой деформации пружин, мембран. Любые формы энергии, превращаясь друг в друга посредством механического движения, химических реакций и электромагнитных излучений, в конце концов, переходят в тепло и рассеиваются в окружающее пространство. Это явление проявляется в виде взрывных процессов, горения, гниения, плавления, испарения, деформации, радиоактивного распада. Происходит круговорот энергии в природе, характеризующийся тем, что в космическом пространстве реализуется не только хаотизация, но и обратный ей процесс — упорядочивание структуры, которые наглядно прослеживаются, прежде всего, в звездообразовании, трансформации и возникновении новых электромагнитных и гравитационных полей. Центральный удар шаров. Упругий удар. Абсолютно упругим называется такой удар, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии. При таком ударе кинетическая энергия переходит полностью в потенциальную энергию упругой деформации. Затем тела отталкивают друг друга. В итоге потенциальная энергия снова переходит в кинетическую и тела разлетаются с определенными скоростями. Для вычисления скоростей после соударения используем два закона: закон сохранения импульса и закон сохранения энергии (рис. 1.11).
Рис. 1.11. Центральный удар шаров Массы шаров Закон сохранения импульса:
Закон сохранения энергии:
В (1.35) и (1.36) группируем члены с
Делим (1.36') на (1.35'):
Решим (1.35') и (1.37) совместно
Выводы. 1. Если
Рис. 1.12. Положение шаров до удара (а) и после удара (б) 2. Если 3. Удар первого шара о массивную стенку (
4. Удар второго шара о массивную стенку
Если стенка неподвижна, то скорость после удара у шара остается той же самой (по величине) и направлена в противоположную сторону. Абсолют |
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.240.101 (0.02 с.) |

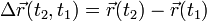 .
.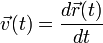 .
.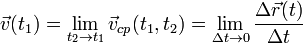 .
.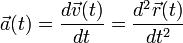 .
. .
.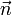 — единичный вектор нормали,
— единичный вектор нормали,  — единичный вектор касательной. Величина
— единичный вектор касательной. Величина 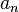 называется нормальным ускорением и характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость и радиус кривизны траектории:
называется нормальным ускорением и характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость и радиус кривизны траектории: .
. называется тангенциальным ускорением и характеризует величину изменения модуля скорости:
называется тангенциальным ускорением и характеризует величину изменения модуля скорости: .
. общая формула пути
общая формула пути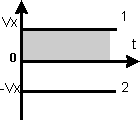

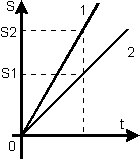







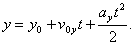
 где r – радиус окружности.
где r – радиус окружности. и тангенциальной
и тангенциальной  составляющих:
составляющих: ,
,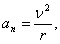
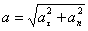 .
.

 (ню) и находится по формуле:
(ню) и находится по формуле:



 .
. . (9.3)
. (9.3) , т. е. сила, с которой тело действует на опору, и сила упругости
, т. е. сила, с которой тело действует на опору, и сила упругости  , с которой опора действует на тело в соответствии с третьим законом Ньютона равны по модулю и противоположны по направлению:
, с которой опора действует на тело в соответствии с третьим законом Ньютона равны по модулю и противоположны по направлению: . (10.1)
. (10.1) и сила упругости
и сила упругости  . (10.2)
. (10.2) , (10.3)
, (10.3) под действием силы тяжести
под действием силы тяжести  выполняется равенство
выполняется равенство . (10.4)
. (10.4) , (10.5)
, (10.5) . (10.6)
. (10.6) и
и  .
. . (10.7)
. (10.7)


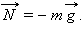 Сила
Сила  с которой тело действует на стол, называется весом тела.
с которой тело действует на стол, называется весом тела.

 — ускорение материальной точки;
— ускорение материальной точки; — сила, приложенная к материальной точке;
— сила, приложенная к материальной точке; — масса материальной точки.
— масса материальной точки.
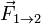 , а второе — на первое с силой
, а второе — на первое с силой  . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются
. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются .
.
 — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил.
— скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил.

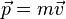 .
.

 и
и  , скорости шаров до удара
, скорости шаров до удара  ,
,  , после удара –
, после удара –  ,
, 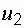 .
. . (1.35)
. (1.35)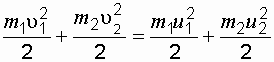 . (1.36)
. (1.36) . (1.35')
. (1.35')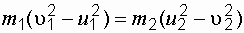 . (1.36')
. (1.36')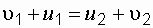 . (1.37)
. (1.37)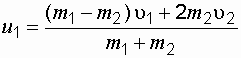 , (1.38)
, (1.38) . (1.39)
. (1.39)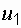 =
=  ,
, 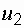 =
=  , т.е. шары обмениваются скоростями после соударения (рис. 1.12).
, т.е. шары обмениваются скоростями после соударения (рис. 1.12).
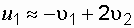 , (1.40)
, (1.40)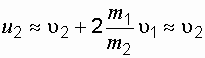 . (1.41)
. (1.41)


