
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равновесие твердого тела при действии плоской системы сил
С.А. Еленев В.Г. Новиков Методические указания по выполнению домашнего индивидуального задания по статике Москва 2006
Данные методические указания является приложением к учебному пособию «СТАТИКА», разработанному С.А. Еленевым, В.Г. Новиковым, Г.И. Шевелевой и выпущенному Издательским Центром МГТУ «Станкин» в 2001 году. В пособии «СТАТИКА» содержится теоретический материал, примеры решения задач и 30 индивидуальных заданий. Каждое индивидуальное задание представляет собой комплект из 7-ми задач по следующим темам: 1. Равновесие твердого тела при действии плоской системы сил. 2. Равновесие плоской механической системы, состоящей из нескольких тел. 3. Степень статической неопределимости плоских механических систем. 4. Равновесие механической системы под действием пространственной системы сил. 5. Приведение пространственной системы сил к центру. 6. Центр тяжести материальной линии. 7. Центр тяжести плоской материальной пластины.
Студент должен получить от преподавателя номер индивидуального задания и решить 7 задач (по одной задаче на каждую из перечисленных тем), условия которых приведены в пособии «СТАТИКА». Ниже приведен пример выполнения индивидуального задания № 30.
Равновесие твердого тела при действии плоской системы сил Задача 1.30. Считая указанную на Рис. 1 к задаче 1.30 нагрузку известной, составить уравнения равновесия для определения реакций. Длины отрезков AB,AC,CD заданы.
Решение. Рассмотрим равновесие тела ABCD. Распределенную по длине BC нагрузку заменим равнодействующей
Выбираем систему координат X,Y и заменяем наложенные на тело связи их реакциями: в неподвижном шарнире A- силами Эти реакции ( Система сил, приложенных к данному телу, эквивалентна нулю, т.е. ( Так как число неизвестных ( Составляем уравнения равновесия:
Равновесие плоской механической системы, Состоящей из нескольких тел
Задача 2.30. Составить уравнения равновесия для определения опорных реакций и давления во внутренних шарнирах A,B,C. (Рис.1 к заданию 2.30) Нагрузка и размеры указанны на рисунке.
Решение. Система, изображенная на Рис.1 к задаче 2.30, находится в равновесии и состоит из четырех тел AD, DC, CE и BE, соединенных внутренними шарнирами D, C, E. Заменим заделки их реакциями: силами По третьей аксиоме механики (действие равно противодействию) реакции
Распределенную нагрузку, приложенную к телу DC заменим одной силой Для каждого из четырех тел системы составим по три уравнения.
Условие равновесия тела AD (Рис.2 к задаче 2.30)
Условие равновесия тела DC (Рис.3 к задаче 2.30)
Условие равновесия тела CE (Рис.4 к задаче 2.30)
Условие равновесия тела BE (Рис.5 к задаче 2.30)
Полученная система двенадцати уравнений позволяет определить все двенадцать неизвестных реакций.
Равновесие механической системы Приведение пространственной системы сил к центру
Задача 5.30. На куб с длиной ребра, равной
Решение. Привести заданную систему сил к центру О - это значит заменить заданную систему одной силой, равной главному вектору, и одной парой сил, момент которой равен главному моменту заданной системы сил, причем главный вектор и главный момент приложены в центре приведения (в точке О). Главный вектор
или в проекциях на декартовы оси координат:
С.А. Еленев В.Г. Новиков Методические указания по выполнению домашнего индивидуального задания по статике Москва 2006
Данные методические указания является приложением к учебному пособию «СТАТИКА», разработанному С.А. Еленевым, В.Г. Новиковым, Г.И. Шевелевой и выпущенному Издательским Центром МГТУ «Станкин» в 2001 году. В пособии «СТАТИКА» содержится теоретический материал, примеры решения задач и 30 индивидуальных заданий. Каждое индивидуальное задание представляет собой комплект из 7-ми задач по следующим темам: 1. Равновесие твердого тела при действии плоской системы сил. 2. Равновесие плоской механической системы, состоящей из нескольких тел. 3. Степень статической неопределимости плоских механических систем. 4. Равновесие механической системы под действием пространственной системы сил. 5. Приведение пространственной системы сил к центру. 6. Центр тяжести материальной линии. 7. Центр тяжести плоской материальной пластины.
Студент должен получить от преподавателя номер индивидуального задания и решить 7 задач (по одной задаче на каждую из перечисленных тем), условия которых приведены в пособии «СТАТИКА». Ниже приведен пример выполнения индивидуального задания № 30.
Равновесие твердого тела при действии плоской системы сил Задача 1.30. Считая указанную на Рис. 1 к задаче 1.30 нагрузку известной, составить уравнения равновесия для определения реакций. Длины отрезков AB,AC,CD заданы.
Решение. Рассмотрим равновесие тела ABCD. Распределенную по длине BC нагрузку заменим равнодействующей
Выбираем систему координат X,Y и заменяем наложенные на тело связи их реакциями: в неподвижном шарнире A- силами Эти реакции ( Система сил, приложенных к данному телу, эквивалентна нулю, т.е. ( Так как число неизвестных ( Составляем уравнения равновесия:
|
|||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.67.25 (0.009 с.) |

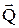 . По величине
. По величине  и приложена на расстояние
и приложена на расстояние  от точки В. (Рис. 2)
от точки В. (Рис. 2)
 в идеальном стержне B - силой
в идеальном стержне B - силой 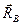 .
. ) предварительно направляем в положительные стороны координатных осей. Если величины реакций окажутся отрицательными, то это будет означать, что их истинные направления противоположны.
) предварительно направляем в положительные стороны координатных осей. Если величины реакций окажутся отрицательными, то это будет означать, что их истинные направления противоположны.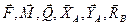 )~0.
)~0. ) равно трем и число уравнений равновесия данной плоской произвольной системы равно трем, то задача статически определима.
) равно трем и число уравнений равновесия данной плоской произвольной системы равно трем, то задача статически определима.

 и реактивными моментами
и реактивными моментами 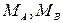 . Расчленим систему в шарнирах D,C,E и заменим их внутренними реактивными силами
. Расчленим систему в шарнирах D,C,E и заменим их внутренними реактивными силами 
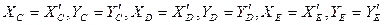 .
. - равнодействующей. Причем сила
- равнодействующей. Причем сила 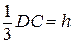 от точки С и равна:
от точки С и равна:  ;
;

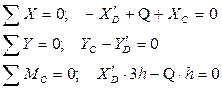





 = 1 м, действует несколько сил, каждая из которых равна 1 Н, и несколько пар сил, моменты которых равны 1 Нм. Привести заданную систему сил к центру О (рис.1 к задаче 5.30).
= 1 м, действует несколько сил, каждая из которых равна 1 Н, и несколько пар сил, моменты которых равны 1 Нм. Привести заданную систему сил к центру О (рис.1 к задаче 5.30). равен геометрической сумме всех сил системы:
равен геометрической сумме всех сил системы: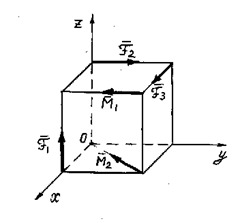 Рис.1
Рис.1
 ,
, ;
; ;
; .
.


