
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциальная энергия - это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Часто взаимодействие тел осуществляется посредством силовых полей (поля гравитации, поля упругих сил и т.д.). Эти поля характеризуются тем, что работа по перемещению тела из одного положения в другое не зависит от траектории перемещения, а зависит только от начального и конечного положений тела. Такие поля называются потенциальными, а силы, действующие на тело - консервативными. Работа консервативных сил по замкнутой траектории равна 0. Если работа, совершаемая силой, зависит от формы траектории тела, то такая сила называется диссипативной (например, сила трения). Работа, совершаемая против диссипативных сил, превращает механическую энергию в тепловую. Работа консервативной силы равна убыли потенциальной энергии Еп. А12 = Еп1 – Еп2 - работа по перемещению материальной точки из точки 1 в точку 2. Потенциальная энергия тела у поверхности Земли: ЕП = mgh + const Потенциальная энергия в поле тяготения: Потенциальная энергия деформированной пружины: Как следует из приведенных формул, потенциальная энергия Еп оказывается определенной с точностью до некоторой неизвестной постоянной (const). При вычислениях это обстоятельство не имеет большого значения, т.к. во все физические формулы входит либо разность значений Еп, либо производная от функции Еп по координатам. Значения постоянных зависит от выбора нулевого уровня потенциальной энергии. Обычно значения постоянных принимаются равными 0. Это означает, что для силы тяжести Еп=0 при h=0, для поля тяготения ЕПТ =0 при г = ¥, а ЕПу =0 при х=0, т.е. когда пружина не растянута. Полная механическая энергия системы - это энергия механического движения и взаимодействия тел Контрольные вопросы: 1. Что такое потенциальная энергия и потенциальные поля? 2. Что такое консервативные и диссипативные силы? 3. Приведите формулу потенциальной энергии сил тяжести у поверхности Земли. 4. Приведите формулу потенциальной энергии в поле тяготения. 5. Приведите формулу потенциальной энергии деформированной пружины.
6. Чему равна полная механическая энергия системы?
Выберите правильные ответы на поставленные вопросы
Динамика вращения АТТ При изучении вращения АТТ часто пользуются понятием момента инерции. Момент инерции тела – мера инерции твердых тел при вращательном движении. Термин момент всегда связан с вращением, при этом обязательно нужно указывать относительно чего вращается тело.
Момент инерции материальной точки массой Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс "n" материальных точек системы на квадраты их расстояний до рассматриваемой оси.
В случае непрерывного распределения масс эта сумма сводится к интегралу Моменты инерции относительно оси вращения наиболее часто встречающихся тел сведены в таблицу. Таблица моментов инерции некоторых тел относительно оси вращения
Если известен момент инерции тела массой
Моментом силы
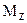 , равная проекции на эту ось вектора момента силы , равная проекции на эту ось вектора момента силы  , определенного относительно произвольной точки О данной оси z. Значение , определенного относительно произвольной точки О данной оси z. Значение  не зависит от выбора положения точки О на оси z. не зависит от выбора положения точки О на оси z.
Моментом импульса тела
 относительно точки О: относительно точки О:  , где , где  - плечо. - плечо.
 Моментом импульса относительно оси z называется скалярная величина Моментом импульса относительно оси z называется скалярная величина  , равная проекции на эту ось вектора момента импульса , равная проекции на эту ось вектора момента импульса 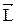 , определенного относительно произвольной точки О данной оси. , определенного относительно произвольной точки О данной оси.
Момент импульса АТТ относительно оси z:

Основной закон динамики вращательного движения АТТ:
Кинетическая энергия вращения тела находится как сумма кинетических энергий его элементарных объемов:
 . Поскольку угловая скорость всех элементарных объемов одна и та же . Поскольку угловая скорость всех элементарных объемов одна и та же  , то: Евр= , то: Евр=  . Таким образом: . Таким образом:
Работа, совершаемая при вращении АТТ, идет на увеличение его кинетической энергии:
В случае плоского движения АТТ его кинетическая энергия складывается из энергии поступательного движения и энергия вращательного движения Ic - момент инерции относительно оси, проходящей через центр масс.
Центром масс системы называется точка С, положение которой задает радиус-вектор
Декартовы координаты центра масс:
В заключении сопоставим в виде таблицы основные величины и уравнения поступательного и вращательного движения тела. В приведенной таблице прослеживается аналогия конфигурации формул для расчета физических величин поступательного и вращательного движений.
Контрольные вопросы: 1. Что такое момент инерции тела? 2. Изложите теорему Штейнера. 3. Расскажите, что Вы знаете о моменте силы? 4. Что Вы знаете о моменте импульса АТТ? 5. Изложите закон динамики вращательного движения АТТ. 6. Как вычислить кинетическую энергию вращения АТТ? 7. Как вычислить кинетическую энергию плоского движения АТТ?
Выберите правильные ответы на поставленные вопросы
Статика
Статикой называется раздел механики, в котором изучаются условия равновесия АТТ. Состоянием равновесия называется такое состояние тела, когда оно покоится, движется прямолинейно и равномерно или равномерно вращается вокруг неподвижной оси, проходящей через центр масс тела. Знание условий равновесия АТТ важно для расчетов машин и механизмов, транспортных средств и различных сооружений. Первое условие равновесия является следствием 2-го закона Ньютона Первое условие равновесия АТТ необходимое, но недостаточное, т.к. АТТ может не только двигаться поступательно, но и вращаться. Второе условие равновесия АТТ получается из основного уравнения динамики вращательного движения АТТ:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.135.237 (0.008 с.) |

 , где m и M – массы тел; r – расстояние между центрами тел; G - гравитационная постоянная. G=6,67 × 10-11 н × м2 × кг -2,
, где m и M – массы тел; r – расстояние между центрами тел; G - гравитационная постоянная. G=6,67 × 10-11 н × м2 × кг -2, , где k - жесткость пружины [ k ] = н/м, х – деформация пружины.
, где k - жесткость пружины [ k ] = н/м, х – деформация пружины.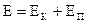 , т.е. равна сумме кинетической и потенциальной энергий.
, т.е. равна сумме кинетической и потенциальной энергий.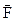 при перемещении
при перемещении  равна…
○ 1. …нулю.
○ 2.
равна…
○ 1. …нулю.
○ 2.  …
…  .
○ 3. …
.
○ 3. …  .
○ 4. …
.
○ 4. …  .
○ 5. …|
.
○ 5. …|  …FdS/cosα.
…FdS/cosα.
 ○ 3.
○ 3.  ○ 4.
○ 4.  ○ 5.
○ 5. 
 V2<V1 t1<t2
○ 2. V2=V1 t1<t2
○ 3. V2>V1 t1=t2
○ 4. V2=V1 t1=t2
V2<V1 t1<t2
○ 2. V2=V1 t1<t2
○ 3. V2>V1 t1=t2
○ 4. V2=V1 t1=t2
 ○ 2.
○ 2.  ○ 3.
○ 3.  ○ 4. необходимо знать другие параметры
○ 4. необходимо знать другие параметры
 относительно оси вращения:
относительно оси вращения:  , где
, где  - кратчайшее расстояние от МТ до оси.
- кратчайшее расстояние от МТ до оси.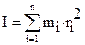
 .
.





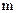 относительно оси, проходящей через его центр масс
относительно оси, проходящей через его центр масс 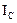 , то момент инерции этого тела
, то момент инерции этого тела  относительно любой другой параллельной оси определяется теоремой Штейнера:
относительно любой другой параллельной оси определяется теоремой Штейнера: , где
, где  - расстояние между осями.
- расстояние между осями.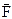 относительно неподвижной точки О (Рисунок 18)называется векторная физическая величина, определяемая векторным произведением радиуса-вектора
относительно неподвижной точки О (Рисунок 18)называется векторная физическая величина, определяемая векторным произведением радиуса-вектора  , проведенного из точки О в точку приложения силы на вектор силы.
, проведенного из точки О в точку приложения силы на вектор силы.  . Вектор
. Вектор 

 Модуль момента силы
Модуль момента силы  , где
, где  - плечо - кратчайшее расстояние между линией действия силы
- плечо - кратчайшее расстояние между линией действия силы  и точкой O.
и точкой O.

 Момент силы относительно оси z равен произведению момента инерции тела относительно этой оси на угловое ускорение - основной закон динамики вращательного движения.
Момент силы относительно оси z равен произведению момента инерции тела относительно этой оси на угловое ускорение - основной закон динамики вращательного движения. При одновременном действии на тело нескольких моментов сил основной закон динамики вращательного движения примет вид:
При одновременном действии на тело нескольких моментов сил основной закон динамики вращательного движения примет вид: .
. относительно неподвижной точки О (Рисунок 20)называется векторная физическая величина, определяемая векторным произведением
относительно неподвижной точки О (Рисунок 20)называется векторная физическая величина, определяемая векторным произведением  .
.
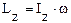



 , где uс - скорость центра масс,
, где uс - скорость центра масс, .
. , где m – масса системы
, где m – масса системы  , mi – масса i-той частицы,
, mi – масса i-той частицы, 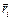 - радиус - вектор i-той частицы.
- радиус - вектор i-той частицы. ;
; 
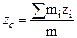

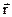 и импульс
и импульс  .
○ 2. …
.
○ 2. …  .
○ 3. …|
.
○ 3. …|  .
○ 4. …
.
○ 4. …  Точка 4.
Точка 4.
 …F^R.
○ 5. …Fh.
…F^R.
○ 5. …Fh.
 Сплошной диск 1 и тонкое кольцо 2 одинаковых масс и радиусов исходно неподвижны. Их начинают синхронно (с одинаковыми угловыми ускорениями) раскручивать вокруг осей симметрии моментами сил M1 и M2 соответственно. Чему равно отношение величин этих моментов M1/M2?
Сплошной диск 1 и тонкое кольцо 2 одинаковых масс и радиусов исходно неподвижны. Их начинают синхронно (с одинаковыми угловыми ускорениями) раскручивать вокруг осей симметрии моментами сил M1 и M2 соответственно. Чему равно отношение величин этих моментов M1/M2?
 Запишите значение
Запишите значение
 - векторная (геометрическая) сумма всех сил равна 0. При решении задачэто условие обычно записывается в виде проекций на координатные оси х и у:
- векторная (геометрическая) сумма всех сил равна 0. При решении задачэто условие обычно записывается в виде проекций на координатные оси х и у: 
 .
.
 где
где  - векторная сумма моментов сил, действующих на АТТ. Из этого уравнения следует второе условие равновесия АТТ:
- векторная сумма моментов сил, действующих на АТТ. Из этого уравнения следует второе условие равновесия АТТ:  - векторная сумма моментов сил относительно любой оси должна быть равна 0. Для плоской системы сил
- векторная сумма моментов сил относительно любой оси должна быть равна 0. Для плоской системы сил  . Моменту сил, стремящихся повернуть тело относительно оси z по часовой стрелке присваивается знак "+", против - знак "–".
. Моменту сил, стремящихся повернуть тело относительно оси z по часовой стрелке присваивается знак "+", против - знак "–".


