
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тепловое излучение. Закон кирхгофаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Глава I Фотоэффект
Схема экспериментальной установки для исследования фотоэффекта изображена на рис. 1.
 очищена. К электродам прикладывалось некоторое напряжение U, полярность которого можно было изменять с помощью двойного ключа. Один из электродов (катод K) через кварцевое окошко освещался монохроматическим светом некоторой длины волны λ. При неизменном световом потоке снималась зависимость силы фототока I от приложенного напряжения. На рис. 2 изображены типичные кривые такой зависимости, полученные при двух значениях интенсивности светового потока, падающего на катод. очищена. К электродам прикладывалось некоторое напряжение U, полярность которого можно было изменять с помощью двойного ключа. Один из электродов (катод K) через кварцевое окошко освещался монохроматическим светом некоторой длины волны λ. При неизменном световом потоке снималась зависимость силы фототока I от приложенного напряжения. На рис. 2 изображены типичные кривые такой зависимости, полученные при двух значениях интенсивности светового потока, падающего на катод.
Кривые показывают, что при достаточно больших положительных напряжениях на аноде A фототок достигает насыщения, так как все электроны, вырванные светом из катода, достигают анода. Тщательные измерения показали, что ток насыщения I н прямо пропорционален интенсивности падающего света. Когда напряжение на аноде отрицательно, электрическое поле между катодом и анодом тормозит электроны. Анода могут достичь только те электроны, кинетическая энергия которых превышает | eU |. Если напряжение на аноде меньше, чем – U з, фототок прекращается. Измеряя U з, можно определить максимальную кинетическую энергию фотоэлектронов: (mυ 2 / 2) max = eU з
 К удивлению ученых, величина U з оказалась независящей от интенсивности падающего светового потока. Тщательные измерения показали, что запирающий потенциал линейно возрастает с увеличением частоты ν света (рис. 3). К удивлению ученых, величина U з оказалась независящей от интенсивности падающего светового потока. Тщательные измерения показали, что запирающий потенциал линейно возрастает с увеличением частоты ν света (рис. 3).
Многочисленными экспериментаторами были установлены следующие основные закономерности фотоэффекта: 1. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с увеличением частоты света ν и не зависит от его интенсивности. 2. Для каждого вещества существует так называемая красная граница фотоэффекта, т. е. наименьшая частота νmin, при которой еще возможен внешний фотоэффект. 3. Число фотоэлектронов, вырываемых светом из катода за 1 с, прямо пропорционально интенсивности света. 4. Фотоэффект практически безынерционен, фототок возникает мгновенно после начала освещения катода при условии, что частота света ν > νmin. Все эти закономерности фотоэффекта в корне противоречили представлениям классической физики о взаимодействии света с веществом. Согласно волновым представлениям при взаимодействии с электромагнитной световой волной электрон должен был бы постепенно накапливать энергию, и потребовалось бы значительное время, зависящее от интенсивности света, чтобы электрон накопил достаточно энергии для того, чтобы вылететь из катода. Как показывают расчеты, это время должно было бы исчисляться минутами или часами. Однако, опыт показывает, что фотоэлектроны появляются немедленно после начала освещения катода. В этой модели также было невозможно понять существование красной границы фотоэффекта. Волновая теория света не могла объяснить независимость энергии фотоэлектронов от интенсивности светового потока и пропорциональность максимальной кинетической энергии частоте света. Таким образом, электромагнитная теория света оказалась неспособной объяснить эти закономерности. Выход был найден А. Эйнштейном в 1905 г. Теоретическое объяснение наблюдаемых закономерностей фотоэффекта было дано Эйнштейном на основе гипотезы М. Планка о том, что свет излучается и поглощается определенными порциями, причем энергия каждой такой порции определяется формулой E = h ν, где h – постоянная Планка. Эйнштейн сделал следующий шаг в развитии квантовых представлений. Он пришел к выводу, что свет имеет прерывистую (дискретную) структуру. Электромагнитная волна состоит из отдельных порций – квантов, впоследствии названных фотонами. При взаимодействии с веществом фотон целиком передает всю свою энергию h ν одному электрону. Часть этой энергии электрон может рассеять при столкновениях с атомами вещества. Кроме того, часть энергии электрона затрачивается на преодоление потенциального барьера на границе металл–вакуум. Для этого электрон должен совершить работу выхода Aвых, зависящую от свойств материала катода. Наибольшая кинетическая энергия, которую может иметь вылетевший из катода фотоэлектрон, определяется законом сохранения энергии:
Эту формулу принято называть уравнением Эйнштейна для фотоэффекта. С помощью уравнения Эйнштейна можно объяснить все закономерности внешнего фотоэффекта. Из уравнения Эйнштейна следуют линейная зависимость максимальной кинетической энергии от частоты и независимость от интенсивности света, существование красной границы, безынерционность фотоэффекта. Общее число фотоэлектронов, покидающих за 1 с поверхность катода, должно быть пропорционально числу фотонов, падающих за то же время на поверхность. Из этого следует, что ток насыщения должен быть прямо пропорционален интенсивности светового потока. Это утверждение носит название закона Столетова. Как следует из уравнения Эйнштейна, тангенс угла наклона прямой, выражающей зависимость запирающего потенциала U з от частоты ν (рис. 3), равен отношению постоянной Планка h к заряду электрона e: Это позволяет экспериментально определить значение постоянной Планка. Такие измерения были выполнены в 1914 г. Р. Милликеном и дали хорошее согласие со значением, найденным Планком. Эти измерения позволили также определить работу выхода A:
где c – скорость света, λкр – длина волны, соответствующая красной границе фотоэффекта. У большинства металлов работа выхода A составляет несколько электрон-вольт (1 эВ = 1,602·10-19 Дж). В квантовой физике электрон-вольт часто используется в качестве энергетической единицы измерения. Значение постоянной Планка, выраженное в электрон–вольтах в секунду, равно h =4.136·10-15 эВ·с. Среди металлов наименьшей работой выхода обладают щелочные элементы. Например, у натрия A = 1,9 эВ, что соответствует красной границе фотоэффекта λкр ≈ 680 нм. Поэтому соединения щелочных металлов используют для создания катодов в фотоэлементах, предназначенных для регистрации видимого света. Итак, законы фотоэффекта свидетельствуют, что свет при испускании и поглощении ведет себя подобно потоку частиц, получивших название фотонов или световых квантов. Таким образом, учение о свете, совершив виток длительностью в два столетия, вновь возвратилось к представлениям о световых частицах – корпускулах. Но это не был механический возврат к корпускулярной теории Ньютона. В начале XX века стало ясно, что свет обладает двойственной природой. При распространении света проявляются его волновые свойства (интерференция, дифракция, поляризация), а при взаимодействии с веществом – корпускулярные (фотоэффект). Эта двойственная природа света получила название корпускулярно-волнового дуализма. Позже двойственная природа была открыта у электронов и других элементарных частиц. Классическая физика не может дать наглядной модели сочетания волновых и корпускулярных свойств у микрообъектов. Движением микрообъектов управляют не законы классической механики Ньютона, а законы квантовой механики. Теория излучения абсолютно черного тела, развитая М. Планком, и квантовая теория фотоэлектрического эффекта Эйнштейна лежат в основании этой современной науки. Кроме рассмотренного нами внешнего фотоэффекта (называемого обычно просто фотоэффектом), существует также внутренний фотоэффект, наблюдаемый в диэлектриках и полупроводниках. Он заключается в обусловленном действием света перераспределении электронов по энергетическим уровням. В этом случае электроны выделяются во всем объеме.
В области р-n перехода или на грани металла с полупроводником может наблюдаться вентильный фотоэффект. Он заключается в возникновении под действием света электродвижущей силы (фото-э.д.с). На рис. 173 показан ход потенциальной энергии электронов (сплошная кривая) и дырок (пунктирная кривая) в области р-n перехода. Неосновные для данной области носители (электроны в р -области и дырки в n -области), возникшие под действием света, проходят через переход. В результате в p -области накапливается избыточный положительный заряд, в n -области — избыточный отрицательный заряд. Это приводит к возникновению приложенного к переходу напряжения, которое и представляет собой фотоэлектродвижущую силу. В частности этот эффект используется при создании солнечных батарей.
Эффект Комптона
 Особенно отчетливо проявляются корпускулярные свойства света в явлении, которое получило название эффекта Комптона. В 1923 г. А. Комптон, исследуя рассеяние рентгеновских лучен различными веществами, обнаружил, что в рассеянных лучах, наряду с излучением первоначальной длины волны λ содержатся также лучи большей длины волны λ '. Разность Δλ = λ – λ ' оказалась зависящей только от угла θ, образуемого направлением рассеянного излучения с направлением первичного пучка. От длины волны λи от природы рассеивающего вещества Δλ не зависит. Особенно отчетливо проявляются корпускулярные свойства света в явлении, которое получило название эффекта Комптона. В 1923 г. А. Комптон, исследуя рассеяние рентгеновских лучен различными веществами, обнаружил, что в рассеянных лучах, наряду с излучением первоначальной длины волны λ содержатся также лучи большей длины волны λ '. Разность Δλ = λ – λ ' оказалась зависящей только от угла θ, образуемого направлением рассеянного излучения с направлением первичного пучка. От длины волны λи от природы рассеивающего вещества Δλ не зависит.
Схема опыта Комптона показана на рис. 11.1. Выделяемый диафрагмами D узкий пучок монохроматического (характеристического) рентгеновского излучения направлялся на рассеивающее вещество Р. Спектральный состав рассеянного излучения исследовался с помощью рентгеновского спектрографа, состоящего из кристалла К и ионизационной камеры. На рис. 11.2 приведены результаты исследования рассеяния монохроматических рентгеновских лучей (линия Кα молибдена) на графите. Кривая θ = 0характеризует первичное излучение. Остальные кривые относятся к разным углам рассеяния, значения которых указаны на рисунке. По оси ординат отложена интенсивность излучения, по оси абсцисс — длина волны.
 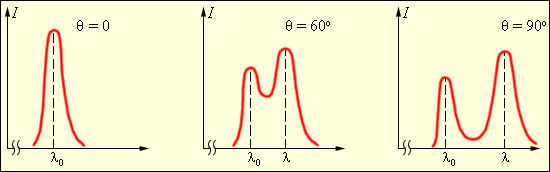
Все особенности эффекта Комптона можно объяснить, рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов с практически свободными электронами. Свободными можно считать слабее всего связанные с атомами электроны, энергия связи которых значительно меньше той энергии, которую фотон может передать электрону при соударении. Поскольку рассеянный электрон летит со скоростью близкой к скорости света, мы должны законы сохранения энергии и импульса применять в релятивистском виде. Пусть на первоначально покоящийся свободный электрон падает фотон с энергией ħω и импульсом p0 (рис.3). Энергия электрона до столкновения равна т0с2 (m0 — масса покоя электрона), импульс равен нулю. После столкновения электрон будет обладать импульсом рe и энергией, равной тс2. Энергия и импульс фотона также изменятся и станут равными ħω ' и p. Из законов сохранения энергии и импульса вытекают два равенства:
ħω + т0с2 = ħω ' + тс2 (1) p0 = рe + p (2)
Для импульса фотона:
p0 = ħ k, p = ħ k', кроме того:
Разделим равенство (1) на с и напишем его в виде
(ω/c=k). Возведение в квадрат дает
Из (2) следует, что
(θ — угол между векторами p 0и p; см. рис. 3). Из сравнения выражений (3) и (4) получаем
Умножим это равенство на 2π и разделим на mckk':
Наконец, учтя, что 2π /k =λ, придем к формуле
Δλ = λ’ – λ = λC(1 – cos θ), (5) где
Определяемая выражением (6) величина λC называется комптоновской длиной волны той частицы, масса т которой имеется в виду. В рассматриваемом нами случае λC — комптоновская длина волны электрона. Подстановка в (6) значений ħ, m 0и с дает для λC электрона значение λC = 0,0243
Результаты измерений Комптона и последующих измерений находятся в полном согласии с формулой (5), если подставить в нее значение (7) для λC. При рассеянии фотонов на электронах, связь которых с атомом велика, обмен энергией и импульсом происходит с атомом как целым. Поскольку масса атома намного превосходит массу электрона, комптоновское смещение в этом случае ничтожно и λ ' практически совпадает с λ.
§ 13. Модель атома Томсона Согласно классическим представлениям атом мог бы испускать монохроматическую волну (т.е. спектральную линию) в том случае, когда электрон в излучающем атоме совершает гармонические колебания и, следовательно, удерживается около положения равновесия квазиупругой силой вида F = – kr, где r — отклонение электрона от положения равновесия. В 1903 г. Томсон предложил модель атома, согласно которой атом представляет собой равномерно заполненный положительным электричеством шар, внутри которого находится электрон (рис. 1). Суммарный положительный заряд шара равен заряду электрона, так что атом в целом нейтрален. Напряженность поля внутри равномерно заряженного шара определяется выражением

В таких условиях электрон, выведенный каким-либо образом из положения равновесия, будет совершать колебания с частотой
(е —заряд электрона, m — масса электрона, R —радиус атома). Этим соотношением можно воспользоваться для оценки размеров атома. Согласно (1)
Длине волны λ = 6000 Å (видимая область спектра) соответствует ω = 3·1015 рад/с. Следовательно,
Полученное значение совпадает по порядку величины с газокинетическими размерами атомов, что можно было бы рассматривать как подтверждение модели Томсона. Однако в дальнейшем выяснилась несостоятельность этой модели, так что в настоящее время она имеет лишь исторический интерес как одно из звеньев в цепи развития представлений о строении атомов. § 14. Опыты по рассеянию α-частиц. Ядерная модель атома
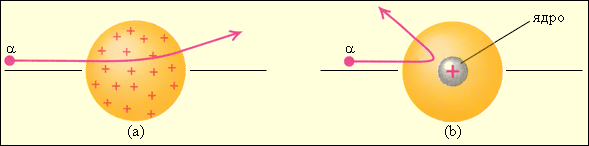
Существовала также и другая модель атома – планетарная. Согласно этой модели в центре атома располагалось положительно заряженное ядро, вокруг которого вращались отрицательно заряженные электроны, подобно планетам, вращающимся вокруг Солнца. Распределение положительных и отрицательных зарядов в атоме можно выяснить, произведя непосредственное опытное «зондирование» внутренних областей атома. Такое зондирование осуществили Резерфорд и его сотрудники с помощью α -частиц, наблюдая изменение направления их полета (рассеяние) при прохождении через тонкие слои вещества.
Рисунок 7 Напомним, что α -частицами называют частицы, испускаемые некоторыми веществами при радиоактивном распаде. Скорости α -частиц бывают порядка 109 см/с. В то время, когда Резерфорд приступал к своим опытам, было известно, что α -частицы имеют положительный заряд, равный удвоенному элементарному заряду, и что при потере этого заряда (при присоединении двух электронов) α –частица превращается в атом гелия. По характеру рассеяния α –частицы можно отдать предпочтение той или иной модели строения атома (рис.2).
Оказалось, что некоторое количество α-частиц рассеивается на очень большие углы (почти до 180°). Проанализировав результаты опыта, Резерфорд пришел к выводу, что столь сильное отклонение α-частиц возможно только в том случае, если внутри атома имеется чрезвычайно сильное электрическое поле, которое создается зарядом, связанным с большой массой и сконцентрированным в очень малом объеме. Основываясь на этом выводе, Резерфорд предложил в 1911 г. ядерную модель атома. Согласно Резерфорду атом представляет собой систему зарядов, в центре которой расположено тяжелое положительное ядро с зарядом Zе, имеющее размеры, не превышающие 10-12 см, а вокруг ядра расположены Z электронов, распределенных по всему объему, занимаемому атомом. Почти вся масса атома сосредоточена в ядре.
В этом случае траектория частицы представляет собой гиперболу. Угол между асимптотами гиперболы обозначим буквой θ (рис. 14.2). Этот угол характеризует отклонение частицы от первоначального направления. Расстояние b от ядра до первоначального направления полета α-частицы называется прицельным параметром. Чем ближе пролетает частица от ядра (чем меньше b), тем, естественно, сильнее она отклоняется (тем больше θ). Между величинами b и θ имеется простое соотношение, которое легко установить решая задачу о движении частицы в центральном поле:
 Рассмотрим слой рассеивающего вещества настолько тонкий, чтобы каждая частица при прохождении через него пролетала вблизи только одного ядра, т. е. чтобы каждая частица претерпевала лишь однократное рассеяние. Для того чтобы испытать рассеяние на угол, лежащий в пределах от θ до θ + dθ, частица должна пролететь вблизи одного из ядер по траектории, прицельный параметр которой заключен в пределах от b до b+db (рис. 4), причем dθ и db, как следует из (1), связаны соотношением Рассмотрим слой рассеивающего вещества настолько тонкий, чтобы каждая частица при прохождении через него пролетала вблизи только одного ядра, т. е. чтобы каждая частица претерпевала лишь однократное рассеяние. Для того чтобы испытать рассеяние на угол, лежащий в пределах от θ до θ + dθ, частица должна пролететь вблизи одного из ядер по траектории, прицельный параметр которой заключен в пределах от b до b+db (рис. 4), причем dθ и db, как следует из (1), связаны соотношением
Знак минус в этом выражении обусловлен тем, что с увеличением b (т.е. при db > 0) угол отклонения убывает (dθ < 0). В дальнейшем нас будет интересовать лишь абсолютное значение db в функции от θ и dθ, поэтому знак минус мы не будем учитывать.
 Обозначим площадь поперечного сечения пучка α-частнц буквой S. Тогда количество атомов рассеивающей фольги на пути пучка можно представить в виде пSа, где п — число атомов в единице объема, а – толщина фольги. Если α-частицы распределены равномерно по сечению пучка и число их очень велико (что имеет место на самом деле), то относительное количество α-частиц, пролетающих вблизи одного из ядер по траектории с прицельным параметром от b до b+db (и, следовательно, отклоняющихся в пределах углов от θ до θ+dθ), будет равно (см. рис. 5): Обозначим площадь поперечного сечения пучка α-частнц буквой S. Тогда количество атомов рассеивающей фольги на пути пучка можно представить в виде пSа, где п — число атомов в единице объема, а – толщина фольги. Если α-частицы распределены равномерно по сечению пучка и число их очень велико (что имеет место на самом деле), то относительное количество α-частиц, пролетающих вблизи одного из ядер по траектории с прицельным параметром от b до b+db (и, следовательно, отклоняющихся в пределах углов от θ до θ+dθ), будет равно (см. рис. 5):
В этом выражении dNθ — поток частиц, рассеиваемых в пределах углов от θ до θ+dθ, N — полный поток частиц в пучке. Заменив в формуле (2) b и db через θ и dθ в соответствии с (1) и (2), получим
Преобразуем множители, содержащие угол θ:
С учетом этого преобразования
Выражение
Справедливость теории, исходящей из кулоновского взаимодействия между α-частицей и ядром атома, свидетельствует о том, что даже отбрасываемая в обратном направлении α-частица не проникает в область положительного заряда атома. Вместе с тем, летящая точно по направлению к ядру α-частица подошла бы кего центру на расстояние, которое можно определить, приравняв кинетическую энергию α-частицы потенциальной энергии взаимодействия α-частицы с ядром в момент полной остановки частицы:
Итак, результаты опытов по рассеянию α-частиц свидетельствуют в пользу ядерной модели атома, предложенной Резерфордом рис.7.
Лазеры
Лазеры или оптические квантовые генераторы – это современные когерентные источники излучения, обладающие целым рядом уникальных свойств. Создание лазеров явилось одним из самых замечательных достижений физики второй половины XX века, которое привело к революционным изменениям во многих областях науки и техники. К настоящему времени создано большое количество лазеров с различными характеристиками – газовых, твердотельных, полупроводниковых, излучающих свет в различных оптических диапазонах. Лазеры могут работать в импульсном и непрерывном режимах. Мощность излучения лазеров может изменяться в пределах от долей милливатта до 1012–1013 Вт (в импульсном режиме). Лазеры находят широкое применение в военной технике, в технологии обработки материалов, в медицине, в оптических системах навигации, связи и локации, в прецизионных интерференционных экспериментах, в химии, просто в быту и т. д. Хотя первый лазер был построен сравнительно недавно (1960 г.), современную жизнь уже невозможно представить без лазеров. Одним из важнейших свойств лазерного излучения является чрезвычайно высокая степень его монохроматичности, недостижимая в излучении нелазерных источников. Это и все другие уникальные свойства лазерного излучения возникают в результате согласованного, кооперативного испускания световых квантов многими атомами рабочего вещества. Чтобы понять принцип работы лазера, нужно более внимательно изучить процессы поглощения и излучения атомами квантов света. Атом может находиться в различных энергетических состояниях с энергиями E 1, E 2 и т. д. В теории Бора эти состояния называются стабильными. На самом деле стабильным состоянием, в котором атом может находиться бесконечно долго в отсутствие внешних возмущений, является только состояние с наименьшей энергией. Это состояние называют основным. Все другие состояния нестабильны. Возбужденный атом может пребывать в этих состояниях лишь очень короткое время, порядка 10–8 с, после этого он самопроизвольно переходит в одно из низших состояний, испуская квант света, частоту которого можно определить из второго постулата Бора. Излучение, испускаемое при самопроизвольном переходе атома из одного состояния в другое, называют спонтанным. На некоторых энергетических уровнях атом может пребывать значительно большее время, порядка 10–3 с. Такие уровни называются метастабильными. Переход атома в более высокое энергетическое состояние может происходить при резонансном поглощении фотона, энергия которого равна разности энергий атома в конечном и начальном состояниях. Переходы между энергетическими уровнями атома не обязательно связаны с поглощением или испусканием фотонов. Атом может приобрести или отдать часть своей энергии и перейти в другое квантовое состояние в результате взаимодействия с другими атомами или столкновений с электронами. Такие переходы называются безизлучательными. Теперь самое главное. В 1916 году А. Эйнштейн предсказал, что переход электрона в атоме с верхнего энергетического уровня на нижний может происходить под влиянием внешнего электромагнитного поля, частота которого равна собственной частоте перехода. Возникающее при этом излучение называют вынужденным или индуцированным. Вынужденное излучение обладает удивительным свойством. Оно резко отличается от спонтанного излучения. В результате взаимодействия возбужденного атома с фотоном атом испускает еще один фотон той же самой частоты, распространяющийся в том же направлении. На языке волновой теории это означает, что атом излучает электромагнитную волну, у которой частота, фаза, поляризация и направление распространения точно такие же, как и у первоначальной волны. В результате вынужденного испускания фотонов амплитуда волны, распространяющейся в среде, возрастает. С точки зрения квантовой теории, в результате взаимодействия возбужденного атома с фотоном, частота которого равна частоте перехода, появляются два совершенно одинаковых фотона-близнеца. Именно индуцированное излучение является физической основой работы лазеров. На рис. 9.4.1 схематически представлены возможные механизмы переходов между двумя энергетическими состояниями атома с поглощением или испусканием кванта.
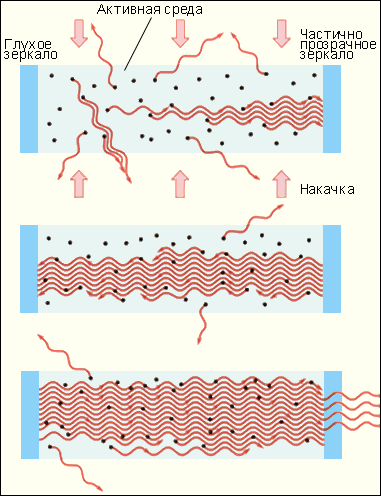
Рассмотрим слой прозрачного вещества, атомы которого могут находиться в состояниях с энергиями E 1 и E 2 > E 1. Пусть в этом слое распространяется излучение резонансной частоты перехода ν = ΔE / h. Согласно распределению Больцмана, при термодинамическом равновесии большее количество атомов вещества будет находиться в нижнем энергетическом состоянии. Некоторая часть атомов будет находиться и в верхнем энергетическом состоянии, получая необходимую энергию при столкновениях с другими атомами. Обозначим населенности нижнего и верхнего уровней соответственно через n 1 и n 2 < n 1. При распространении резонансного излучения в такой среде будут происходить все три процесса, изображенные на рис. 1. Эйнштейн показал, что процесс (a) поглощения фотона невозбужденным атомом и процесс (c) индуцированного испускания кванта возбужденным атомом имеют одинаковые вероятности. Так как n 2 < n 1 поглощение фотонов будет происходить чаще, чем индуцированное испускание. В результате прошедшее через слой вещества излучение будет ослабляться. Это явление напоминает появление темных фраунгоферовских линий в спектре солнечного излучения. Излучение, возникающее в результате спонтанных переходов, некогерентно и распространяется во всевозможных направлениях и не дает вклада в проходящую волну. Чтобы проходящая через слой вещества волна усиливалась, нужно искусственно создать условия, при которых n 2 > n 1, то есть создать инверсную населенность уровней. Такая среда является термодинамически неравновесной. Идея использования неравновесных сред для получения оптического усиления впервые была высказана В. А. Фабрикантом в 1940 году. В 1954 году советские физики Н. Г. Басов и А. М. Прохоров и независимо от них американский ученый Ч. Таунс использовали явление индуцированного испускания для создания микроволнового генератора радиоволн с длиной волны λ = 1,27 см. За разработку нового принципа усиления и генерации радиоволн в 1964 году все трое были удостоены Нобелевской премии. Среда, в которой создана инверсная населенность уровней, называется активной. Она может служить резонансным усилителем светового сигнала. Для того, чтобы возникала генерация света, необходимо использовать обратную связь. Для этого активную среду нужно расположить между двумя высококачественными зеркалами, отражающими свет строго назад, чтобы он многократно прошел через активную среду, вызывая лавинообразный процесс индуцированной эмиссии когерентных фотонов. При этом в среде должна поддерживаться инверсная населенность уровней. Этот процесс в лазерной физике принято называть накачкой. Начало лавинообразному процессу в такой системе при определенных условиях может положить случайный спонтанный акт, при котором возникает излучение, направленное вдоль оси системы. Через некоторое время в такой системе возникает стационарный режим генерации. Это и есть лазер. Лазерное излучение выводится наружу через одно (или оба) из зеркал, обладающее частичной прозрачностью. На рис. 2 схематически представлено развитие лавинообразного процесса в лазере.
Существуют различные способы получения среды с инверсной населенностью уровней. В рубиновом лазере используется оптическая накачка. Атомы возбуждаются за счет поглощения света. Но для этого недостаточно только двух уровней. Каким бы мощным не был свет лампы–накачки, число возбужденных атомов не будет больше числа невозбужденных. В рубиновом лазере накачка производится через третий выше расположенный уровень (рис. 3).
После вспышки мощной лампы, расположенной рядом с рубиновым стержнем, многие атомы хрома, входящего в виде примеси в кристалл рубина (около 0,05 %), переходят в состояние с энергией E 3, а через промежуток τ ≈ 10–8 с они переходят в состояние с энергией E 2. Перенаселенность возбужденного уровня E 2 по сравнению с невозбужденным уровнем E 1 возникает из-за относительно большого времени жизни уровня E 2. Лазер на рубине работает в импульсном режиме на длине волны 694 мм (темно-вишневый свет), мощность излучения может достигать в импульсе 106–109 Вт. Исторически это был первый действующий лазер (американский физик Т. Майман, 1960 г.). Одним из самых распространенных лазеров в настоящее время является газовый лазер на смеси гелия и неона. Общее давление в смеси составляет порядка 102 Па при соотношении компонент He и Ne примерно 10: 1. Активным газом, на котором возникает генерация на длине волны 632,8 нм (ярко-красный свет) в непрерывном режиме, является неон. Гелий является буферным газом, он участвует в механизме создания инверсной населенности одного из верхних уровней неона. Излучение He–Ne лазера обладает исключительной, непревзойденной монохроматичностью. Расчеты показывают, что спектральная ширина линии генерации He–Ne лазера со
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 922; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.014 с.) |

 Фотоэлектрический эффект был открыт в 1887 году немецким физиком Г. Герцем и в 1888–1890 годах экспериментально исследован А. Г. Столетовым. Наиболее полное исследование явления фотоэффекта было выполнено Ф. Ленардом в 1900 г. К этому времени уже был открыт электрон (1897 г., Дж. Томсон), и стало ясно, что фотоэффект (или точнее – внешний фотоэффект) состоит в вырывании электронов из вещества под действием падающего на него света.
Фотоэлектрический эффект был открыт в 1887 году немецким физиком Г. Герцем и в 1888–1890 годах экспериментально исследован А. Г. Столетовым. Наиболее полное исследование явления фотоэффекта было выполнено Ф. Ленардом в 1900 г. К этому времени уже был открыт электрон (1897 г., Дж. Томсон), и стало ясно, что фотоэффект (или точнее – внешний фотоэффект) состоит в вырывании электронов из вещества под действием падающего на него света.

 На внутреннем фотоэффекте основано действие так называемых фотосопротивлений. Количество образующихся носителей тока пропорционально падающему световому потоку. Поэтому фотосопротивления применяются для целей фотометрии. Первым полупроводником, нашедшим применение для этих целей, был селен.
На внутреннем фотоэффекте основано действие так называемых фотосопротивлений. Количество образующихся носителей тока пропорционально падающему световому потоку. Поэтому фотосопротивления применяются для целей фотометрии. Первым полупроводником, нашедшим применение для этих целей, был селен. 

 (3)
(3)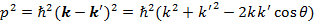 (4)
(4)
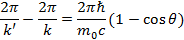

 (7)
(7)
 где е— заряд шара, R — его радиус. Следовательно, на электрон, находящийся на расстоянии r от положения равновесия (от центра шара), будет действовать сила:
где е— заряд шара, R — его радиус. Следовательно, на электрон, находящийся на расстоянии r от положения равновесия (от центра шара), будет действовать сила:







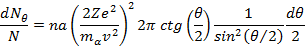


 дает телесный угол dΩ, в пределах которого заключены направления, соответствующие углам рассеяния от θ до θ+dθ. Поэтому можно написать:
дает телесный угол dΩ, в пределах которого заключены направления, соответствующие углам рассеяния от θ до θ+dθ. Поэтому можно написать:
 Мы получили формулу Резерфорда для рассеяния α-частиц. В 1913 г. сотрудники Резерфорда произвели проверку этой формулы путем подсчета сцинтилляций, наблюдавшихся под разными углами θ за одинаковые промежутки времени. В условиях опыта (см. рис. 3) счету подвергались α-частицы, заключенные в пределах одного и того же телесного угла (определявшегося площадью экрана Э и расстоянием его от фольги), поэтому число сцинтилляций, наблюдавшихся под разными углами, должно было быть, в соответствии с формулой Резерфорда, пропорционально
Мы получили формулу Резерфорда для рассеяния α-частиц. В 1913 г. сотрудники Резерфорда произвели проверку этой формулы путем подсчета сцинтилляций, наблюдавшихся под разными углами θ за одинаковые промежутки времени. В условиях опыта (см. рис. 3) счету подвергались α-частицы, заключенные в пределах одного и того же телесного угла (определявшегося площадью экрана Э и расстоянием его от фольги), поэтому число сцинтилляций, наблюдавшихся под разными углами, должно было быть, в соответствии с формулой Резерфорда, пропорционально 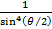 . Этот результат теории хорошо подтвердился на опыте. Зависимость рассеяния от толщины фольги и скорости α-частиц также оказалась -в соответствии с формулой (4).
. Этот результат теории хорошо подтвердился на опыте. Зависимость рассеяния от толщины фольги и скорости α-частиц также оказалась -в соответствии с формулой (4).

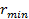 - минимальное расстояние между центрами α-частицы и ядра,
- минимальное расстояние между центрами α-частицы и ядра,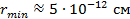 .
. 1
1
 2
2
 3
3



