
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механика теории относительности.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Рассуждения, приведенные выше, показывают, что оптические (и электромагнитные) явления подтверждают кинематику теории относительности, вытекающую из преобразований Лоренца. Естественно ожидать, что эти кинематические законы, дающие пространственно-временную характеристику явлений, должны быть одинаковыми для всех явлений природы. Поскольку преобразования Галилея, относительно которых инвариантны законы ньютоновской механики, являются предельными выражениями преобразований Лоренца, при стремлении отношения υ/'с к нулю, можно думать, что уравнения механики Ньютона также являются предельными уравнениями некоторых более общих уравнений, инвариантных по отношению к преобразованиям Лоренца, как того требует теория относительности. Найти вид уравнений механики теории относительности можно, внеся в уравнения Ньютона такие изменения, которые делают их инвариантными по отношению к преобразованиям Лоренца. Напишем уравнение механики Ньютона в векторной форме:
В механике Ньютона масса т считается величиной постоянной, независящей от состояния движения. Как можно показать, это предположение не совместимо с требованием инвариантности уравнений по отношению к преобразованию Лоренца. Требование, чтобы в механике теории относительности, как и в механике Ньютона, для изолированной системы тел выполнялся в любой системе закон сохранения количества движения и учет законов преобразования скоростей при переходе из одной системы в другую, приводит к выводу, что масса тела должна иметь разные значения в разных системах, находящихся в относительном движении. Закон преобразования масс при этом окажется следующим: m = m0 / Здесь т0 есть значение массы, измеренной в системе, в которой она покоится, а т — значение той же массы, измеренной в системе, движущейся относительно первой с постоянной скоростью υ. Уравнения механики окажутся инвариантными по отношению к преобразованиям Лоренца, если в формуле (1) под массой т подразумевать величину, преобразующуюся по закону (2). Таким образом, уравнения механики теории относительности принимают форму:
Очевидно, что эти уравнения, отличающиеся от уравнений Ньютона, должны приводить к иным следствиям, чем уравнения классической механики. Проверка этих следствий на опыте является проверкой и самих уравнений. Как известно, в классической механике уравнение движения может быть записано в виде: p = m0 v / Исключительно важным следствием механики теории относительности является вытекающая из нее связь между энергией и массой. Установим это соотношение, основываясь на формуле (3). В классической механике изменение кинетической энергии материальной точки определяется по работе, совершенной силами, приложенными к точке. Проведем соответственное рассмотрение для уравнения (3). Элементарная работа dА силы f равна скалярному произведению силы на перемещение d r точки: dA= f · d r. Эта величина должна давать приращение кинетической энергии точки: dA =dEk. На основании формулы (3) имеем: dEk = dA = Выполняя дифференцирование, получим:
или, так как d r / dt равно скорости v, то
Следовательно:
С другой стороны, по формуле (2) находим:
Из сопоставления двух последних формул получаем следующую связь между dEk и dт: dEk = c 2 dm (5) Изменение энергии пропорционально изменению массы, причем коэффициентом пропорциональности является квадрат скорости света. Это положение естественно обобщить, считая что между энергией Е и массой т имеется общая связь, выражаемая соотношением: Е = тс 2(5а) Масса и энергия являются характеристиками качественно различных свойств тех видов материи, которые рассматривает физика. Масса характеризует инерционные свойства материи (второй закон Ньютона) и свойства, проявляющиеся в явлениях всемирного тяготения. Энергия является величиной, изменение которой определяет совершаемые системой работы. Вытекающие из теории относительности соотношения (5) и (5а) указывают, что между этими двумя характеристиками имеет место связь: изменение одной из них ведет к эквивалентному изменению другой. Изменение массы системы может произойти не только за счет обмена с внешними телами веществом (атомами, молекулами), но и за счет передачи системе энергии. Например, если системе передается количество тепла Δ Q, в результате чего ее энергия возрастает на величину Δ Е, то в соответствии с соотношением (5) одновременно возрастает и масса системы на величину Δ m=ΔE/c 2. Другой пример: если в результате излучения света энергия системы убывает на Δ Е, то одновременно уменьшается ее масса на величину Δ m=ΔE/c 2. Для замкнутой системы сохраняется ее масса и сохраняется ее полная энергия. Ввиду большого численного значения скорости света с в пустоте, определенному численному изменению энергии Δ Е соответствует малое изменение массы Δ m. При увеличении энергии системы Е на 1 дж ее масса увеличивается лишь на Δ m ≈ 1,1 • 10-14 г. Поэтому при обычных изменениях энергии тел изменение их массы настолько мало, что оно не может быть непосредственно замечено. Однако современная физика имеет возможность проверить соотношение между энергией и массой, благодаря огромным количествам энергии, освобождаемым при ядерных превращениях. Из соотношения между энергией и массой вытекает релятивистская форма связи между энергией и количеством движения. Подставив в (5а) вместо т его значение по (2), получим:
возводя это равенство в квадрат и производя алгебраические преобразования, найдем:
или на основании (4):
Эффект Комптона
 Особенно отчетливо проявляются корпускулярные свойства света в явлении, которое получило название эффекта Комптона. В 1923 г. А. Комптон, исследуя рассеяние рентгеновских лучен различными веществами, обнаружил, что в рассеянных лучах, наряду с излучением первоначальной длины волны λ содержатся также лучи большей длины волны λ '. Разность Δλ = λ – λ ' оказалась зависящей только от угла θ, образуемого направлением рассеянного излучения с направлением первичного пучка. От длины волны λи от природы рассеивающего вещества Δλ не зависит. Особенно отчетливо проявляются корпускулярные свойства света в явлении, которое получило название эффекта Комптона. В 1923 г. А. Комптон, исследуя рассеяние рентгеновских лучен различными веществами, обнаружил, что в рассеянных лучах, наряду с излучением первоначальной длины волны λ содержатся также лучи большей длины волны λ '. Разность Δλ = λ – λ ' оказалась зависящей только от угла θ, образуемого направлением рассеянного излучения с направлением первичного пучка. От длины волны λи от природы рассеивающего вещества Δλ не зависит.
Схема опыта Комптона показана на рис. 11.1. Выделяемый диафрагмами D узкий пучок монохроматического (характеристического) рентгеновского излучения направлялся на рассеивающее вещество Р. Спектральный состав рассеянного излучения исследовался с помощью рентгеновского спектрографа, состоящего из кристалла К и ионизационной камеры. На рис. 11.2 приведены результаты исследования рассеяния монохроматических рентгеновских лучей (линия Кα молибдена) на графите. Кривая θ = 0характеризует первичное излучение. Остальные кривые относятся к разным углам рассеяния, значения которых указаны на рисунке. По оси ординат отложена интенсивность излучения, по оси абсцисс — длина волны.
 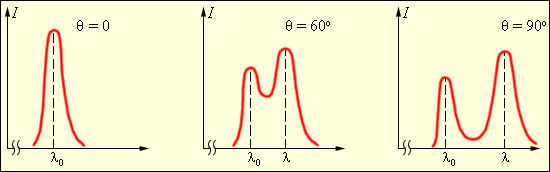
Все особенности эффекта Комптона можно объяснить, рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов с практически свободными электронами. Свободными можно считать слабее всего связанные с атомами электроны, энергия связи которых значительно меньше той энергии, которую фотон может передать электрону при соударении. Поскольку рассеянный электрон летит со скоростью близкой к скорости света, мы должны законы сохранения энергии и импульса применять в релятивистском виде. Пусть на первоначально покоящийся свободный электрон падает фотон с энергией ħω и импульсом p0 (рис.3). Энергия электрона до столкновения равна т0с2 (m0 — масса покоя электрона), импульс равен нулю. После столкновения электрон будет обладать импульсом рe и энергией, равной тс2. Энергия и импульс фотона также изменятся и станут равными ħω ' и p. Из законов сохранения энергии и импульса вытекают два равенства:
ħω + т0с2 = ħω ' + тс2 (1) p0 = рe + p (2)
Для импульса фотона:
p0 = ħ k, p = ħ k', кроме того:
Разделим равенство (1) на с и напишем его в виде
(ω/c=k). Возведение в квадрат дает
Из (2) следует, что
(θ — угол между векторами p 0и p; см. рис. 3). Из сравнения выражений (3) и (4) получаем
Умножим это равенство на 2π и разделим на mckk':
Наконец, учтя, что 2π /k =λ, придем к формуле
Δλ = λ’ – λ = λC(1 – cos θ), (5) где
Определяемая выражением (6) величина λC называется комптоновской длиной волны той частицы, масса т которой имеется в виду. В рассматриваемом нами случае λC — комптоновская длина волны электрона. Подстановка в (6) значений ħ, m 0и с дает для λC электрона значение λC = 0,0243
Результаты измерений Комптона и последующих измерений находятся в полном согласии с формулой (5), если подставить в нее значение (7) для λC. При рассеянии фотонов на электронах, связь которых с атомом велика, обмен энергией и импульсом происходит с атомом как целым. Поскольку масса атома намного превосходит массу электрона, комптоновское смещение в этом случае ничтожно и λ ' практически совпадает с λ.
§ 13. Модель атома Томсона Согласно классическим представлениям атом мог бы испускать монохроматическую волну (т.е. спектральную линию) в том случае, когда электрон в излучающем атоме совершает гармонические колебания и, следовательно, удерживается около положения равновесия квазиупругой силой вида F = – kr, где r — отклонение электрона от положения равновесия. В 1903 г. Томсон предложил модель атома, согласно которой атом представляет собой равномерно заполненный положительным электричеством шар, внутри которого находится электрон (рис. 1). Суммарный положительный заряд шара равен заряду электрона, так что атом в целом нейтрален. Напряженность поля внутри равномерно заряженного шара определяется выражением

В таких условиях электрон, выведенный каким-либо образом из положения равновесия, будет совершать колебания с частотой
(е —заряд электрона, m — масса электрона, R —радиус атома). Этим соотношением можно воспользоваться для оценки размеров атома. Согласно (1)
Длине волны λ = 6000 Å (видимая область спектра) соответствует ω = 3·1015 рад/с. Следовательно,
Полученное значение совпадает по порядку величины с газокинетическими размерами атомов, что можно было бы рассматривать как подтверждение модели Томсона. Однако в дальнейшем выяснилась несостоятельность этой модели, так что в настоящее время она имеет лишь исторический интерес как одно из звеньев в цепи развития представлений о строении атомов. § 14. Опыты по рассеянию α-частиц. Ядерная модель атома
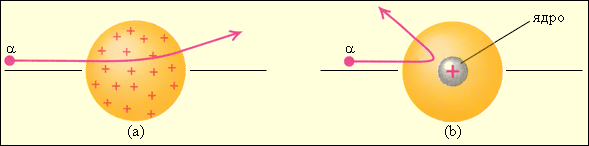
Существовала также и другая модель атома – планетарная. Согласно этой модели в центре атома располагалось положительно заряженное ядро, вокруг которого вращались отрицательно заряженные электроны, подобно планетам, вращающимся вокруг Солнца. Распределение положительных и отрицательных зарядов в атоме можно выяснить, произведя непосредственное опытное «зондирование» внутренних областей атома. Такое зондирование осуществили Резерфорд и его сотрудники с помощью α -частиц, наблюдая изменение направления их полета (рассеяние) при прохождении через тонкие слои вещества.
Рисунок 7 Напомним, что α -частицами называют частицы, испускаемые некоторыми веществами при радиоактивном распаде. Скорости α -частиц бывают порядка 109 см/с. В то время, когда Резерфорд приступал к своим опытам, было известно, что α -частицы имеют положительный заряд, равный удвоенному элементарному заряду, и что при потере этого заряда (при присоединении двух электронов) α –частица превращается в атом гелия. По характеру рассеяния α –частицы можно отдать предпочтение той или иной модели строения атома (рис.2).
Оказалось, что некоторое количество α-частиц рассеивается на очень большие углы (почти до 180°). Проанализировав результаты опыта, Резерфорд пришел к выводу, что столь сильное отклонение α-частиц возможно только в том случае, если внутри атома имеется чрезвычайно сильное электрическое поле, которое создается зарядом, связанным с большой массой и сконцентрированным в очень малом объеме. Основываясь на этом выводе, Резерфорд предложил в 1911 г. ядерную модель атома. Согласно Резерфорду атом представляет собой систему зарядов, в центре которой расположено тяжелое положительное ядро с зарядом Zе, имеющее размеры, не превышающие 10-12 см, а вокруг ядра расположены Z электронов, распределенных по всему объему, занимаемому атомом. Почти вся масса атома сосредоточена в ядре.
В этом случае траектория частицы представляет собой гиперболу. Угол между асимптотами гиперболы обозначим буквой θ (рис. 14.2). Этот угол характеризует отклонение частицы от первоначального направления. Расстояние b от ядра до первоначального направления полета α-частицы называется прицельным параметром. Чем ближе пролетает частица от ядра (чем меньше b), тем, естественно, сильнее она отклоняется (тем больше θ). Между величинами b и θ имеется простое соотношение, которое легко установить решая задачу о движении частицы в центральном поле:
 Рассмотрим слой рассеивающего вещества настолько тонкий, чтобы каждая частица при прохождении через него пролетала вблизи только одного ядра, т. е. чтобы каждая частица претерпевала лишь однократное рассеяние. Для того чтобы испытать рассеяние на угол, лежащий в пределах от θ до θ + dθ, частица должна пролететь вблизи одного из ядер по траектории, прицельный параметр которой заключен в пределах от b до b+db (рис. 4), причем dθ и db, как следует из (1), связаны соотношением Рассмотрим слой рассеивающего вещества настолько тонкий, чтобы каждая частица при прохождении через него пролетала вблизи только одного ядра, т. е. чтобы каждая частица претерпевала лишь однократное рассеяние. Для того чтобы испытать рассеяние на угол, лежащий в пределах от θ до θ + dθ, частица должна пролететь вблизи одного из ядер по траектории, прицельный параметр которой заключен в пределах от b до b+db (рис. 4), причем dθ и db, как следует из (1), связаны соотношением
Знак минус в этом выражении обусловлен тем, что с увеличением b (т.е. при db > 0) угол отклонения убывает (dθ < 0). В дальнейшем нас будет интересовать лишь абсолютное значение db в функции от θ и dθ, поэтому знак минус мы не будем учитывать.
 Обозначим площадь поперечного сечения пучка α-частнц буквой S. Тогда количество атомов рассеивающей фольги на пути пучка можно представить в виде пSа, где п — число атомов в единице объема, а – толщина фольги. Если α-частицы распределены равномерно по сечению пучка и число их очень велико (что имеет место на самом деле), то относительное количество α-частиц, пролетающих вблизи одного из ядер по траектории с прицельным параметром от b до b+db (и, следовательно, отклоняющихся в пределах углов от θ до θ+dθ), будет равно (см. рис. 5): Обозначим площадь поперечного сечения пучка α-частнц буквой S. Тогда количество атомов рассеивающей фольги на пути пучка можно представить в виде пSа, где п — число атомов в единице объема, а – толщина фольги. Если α-частицы распределены равномерно по сечению пучка и число их очень велико (что имеет место на самом деле), то относительное количество α-частиц, пролетающих вблизи одного из ядер по траектории с прицельным параметром от b до b+db (и, следовательно, отклоняющихся в пределах углов от θ до θ+dθ), будет равно (см. рис. 5):
В этом выражении dNθ — поток частиц, рассеиваемых в пределах углов от θ до θ+dθ, N — полный поток частиц в пучке. Заменив в формуле (2) b и db через θ и dθ в соответствии с (1) и (2), получим
Преобразуем множители, содержащие угол θ:
С учетом этого преобразования
Выражение
Справедливость теории, исходящей из кулоновского взаимодействия между α-частицей и ядром атома, свидетельствует о том, что даже отбрасываемая в обратном направлении α-частица не проникает в область положительного заряда атома. Вместе с тем, летящая точно по направлению к ядру α-частица подошла бы кего центру на расстояние, которое можно определить, приравняв кинетическую энергию α-частицы потенциальной энергии взаимодействия α-частицы с ядром в момент полной остановки частицы:
Итак, результаты опытов по рассеянию α-частиц свидетельствуют в пользу ядерной модели атома, предложенной Резерфордом рис.7.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 737; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |

 (m v) = f (1)
(m v) = f (1) (2)
(2) v) = f (3)
v) = f (3) p = f, где, р — количество движения. Сравнивая его с (3), видим, что в механике теории относительности роль количества движения играет величина:
p = f, где, р — количество движения. Сравнивая его с (3), видим, что в механике теории относительности роль количества движения играет величина: v) · d r
v) · d r
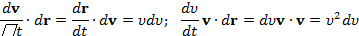







 (3)
(3)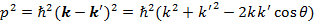 (4)
(4)
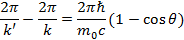

 (7)
(7)
 где е— заряд шара, R — его радиус. Следовательно, на электрон, находящийся на расстоянии r от положения равновесия (от центра шара), будет действовать сила:
где е— заряд шара, R — его радиус. Следовательно, на электрон, находящийся на расстоянии r от положения равновесия (от центра шара), будет действовать сила:







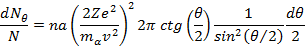


 дает телесный угол dΩ, в пределах которого заключены направления, соответствующие углам рассеяния от θ до θ+dθ. Поэтому можно написать:
дает телесный угол dΩ, в пределах которого заключены направления, соответствующие углам рассеяния от θ до θ+dθ. Поэтому можно написать:
 Мы получили формулу Резерфорда для рассеяния α-частиц. В 1913 г. сотрудники Резерфорда произвели проверку этой формулы путем подсчета сцинтилляций, наблюдавшихся под разными углами θ за одинаковые промежутки времени. В условиях опыта (см. рис. 3) счету подвергались α-частицы, заключенные в пределах одного и того же телесного угла (определявшегося площадью экрана Э и расстоянием его от фольги), поэтому число сцинтилляций, наблюдавшихся под разными углами, должно было быть, в соответствии с формулой Резерфорда, пропорционально
Мы получили формулу Резерфорда для рассеяния α-частиц. В 1913 г. сотрудники Резерфорда произвели проверку этой формулы путем подсчета сцинтилляций, наблюдавшихся под разными углами θ за одинаковые промежутки времени. В условиях опыта (см. рис. 3) счету подвергались α-частицы, заключенные в пределах одного и того же телесного угла (определявшегося площадью экрана Э и расстоянием его от фольги), поэтому число сцинтилляций, наблюдавшихся под разными углами, должно было быть, в соответствии с формулой Резерфорда, пропорционально 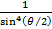 . Этот результат теории хорошо подтвердился на опыте. Зависимость рассеяния от толщины фольги и скорости α-частиц также оказалась -в соответствии с формулой (4).
. Этот результат теории хорошо подтвердился на опыте. Зависимость рассеяния от толщины фольги и скорости α-частиц также оказалась -в соответствии с формулой (4).

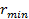 - минимальное расстояние между центрами α-частицы и ядра,
- минимальное расстояние между центрами α-частицы и ядра,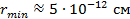 .
.


