
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Физические основы механикиСодержание книги
Поиск на нашем сайте
А.Е. Бурученко Ф И З И К А Часть 1
Красноярск, 2003
УДК 531/534+536 ББК 22.3 Б 91
Рецензенты: А.В. Машуков, канд. физ.-мат. наук, зав.кафедрой физики КГАЦМиЗ, Н.Ф. Шемяков, канд. физ.-мат. наук, доц. КГТУ.
Бурученко А.Е. Б 91. ISBN 5-89628-098-Х
Физика: Учеб. пособие. Ч. 1 / КрасГАСА. Красноярск, 2003.
В предлагаемой работе в соответствии с программой общего курса физики для технических вузов излагаются основы механики, молекулярной физики и термодинамики. Особое внимание уделено раскрытию смысла основных физических закономерностей. Подробно рассмотрены вопросы кинематики и динамики поступательного, вращательного и колебательного движений. Учебное пособие может быть использовано студентами дневной и заочной форм обучения.
УДК 531/534+536 ББК 22.3 © КрасГАСА, 2003 г. ISBN 5-89628-098-Х © А.Е. Бурученко, 2003 г.
ВВЕДЕНИЕ Слово "физика" греческого происхождения и первоначально означало науку о природе или естествознание. Теперь физика является лишь одной из наук о природе. Она изучает простейшие и вместе с тем наиболее общие свойства движущейся материи. По современным представлениям материя существует в двух основных формах: в форме вещества и в форме поля. Под веществом мы понимаем элементарные частицы, атомы, молекулы и все тела, состоящие из атомов и молекул. В физике известны такие поля, как гравитационное, электромагнитное (свет, радиоволны) и ядерное. Эти две формы материи не изолированы друг от друга, они могут превращаться друг в друга. Например, гамма-квант при определенных условиях превращается в пару частиц: электрон и позитрон, которые в свою очередь могут превратиться в квант электромагнитного излучения. Материя может существовать только в движении. Движение представляет собой вечную форму бытия материи. Соответственно многообразию явлений природы существует и множество различных видов движения материи. Но среди этого множества можно выделить несколько основных форм, каждая из которых охватывает более или менее широкий круг явлений, родственных в определенном отношении. Это - механическая форма движения, химическая, биологическая и социальная. Физика изучает наиболее простые формы движения, которые являются и наиболее общими (механические, молекулярные и т.д.), электромагнитные, внутриатомные и ядерные явления. Другие, более высокие, формы движения изучаются другими науками, такими, как химия, биология и т.д. Изучение физических явлений начинается с наблюдения, либо с эксперимента. Наблюдение - это изучение явления в природных условиях, в естественной обстановке. Эксперимент - изучение явления в условиях, специально созданных человеком. На основе накопленного экспериментального материала строится гипотеза - научное предположение о механизме явления и связи его с другими явлениями. Но гипотеза требует проверки и доказательств. Некоторые гипотезы противоречат опыту, оказываются ошибочными и отбрасываются при дальнейшем развитии науки (гипотезы эфира, флогистона и др.). Гипотезы, которые выдерживают проверку на опыте и правильно предсказывают ряд явлений, которые ранее не были известны, входят в науку в качестве теорий. Правильная физическая теория дает качественное и количественное объяснение целой области явлений природы с единой точки зрения. Однако процесс познания не ограничивается таким кругом - от опыта к теории и от теории к опыту. Скоро появляются такие факты, объяснение которых не укладывается в рамки старых теорий, и требуют выдвижения новых гипотез. Примером этого является развитие наших знаний о строении вещества. Молекулярно-кинетическая теория вещества, созданная в XIX в., исходила из того, что все тела состоят из мельчайших частиц - атомов, которые находятся в непрерывном движении. Атом - значит неделимый, что в дальнейшем оказалось не так. Новые теории не всегда отрицают старые, в большинстве случаев они включают старые теории как часть, т.е. являются более широкими и всеобъемлющими. Развитие физики тесно связано с развитием человеческого общества, потребностями практики. Известно, что технические потребности привели в свое время к развитию механики. Задача создания автономных тепловых машин вызвала бурное развитие термодинамики. В то же время физика оказывает огромное влияние на технику. Крупные физические открытия приводят к техническим переворотам. Например, открытие Фарадеем явления электромагнитной индукции создало возможность широкого практического использования электромагнитных явлений. Связь между физикой и техникой двухсторонняя. Развитие техники даст физике более точные приборы и более мощные методы исследования. Так, развитие атомной физики позволило использовать в настоящее время атомную энергию в мирных целях. Широкое использование вычислительных машин оказалось возможным только благодаря достижениям физики твердого тела. Основоположник русской физики и химии М.В. Ломоносов сочетал свою научную работу с требованиями практики. Его многочисленные и разнообразные исследования по природе твердых и жидких тел, оптике, атмосферному электричеству были связаны с теми или иными практическими задачами. А.С. Попов использовал открытие Максвелла- теорию электромагнитных процессов - для осуществления радиотелеграфии. Выдающийся ученый Н.В. Жуковский создал основы воздухоплавания. К.Э. Циолковский и И.В. Мещерский много сделали в области ракетной техники. Среди русских физиков были и теоретики, к ним относится Н.А. Умов, Л.А.Келдыш и.т.д. Советская наука в исключительно короткие сроки добилась огромных успехов в таких решающих направлениях развития естествознания, как освоение космоса, физика элементарных частиц, физика плазмы и др. Во всем мире известны имена наших физиков - теоретиков Л.Д. Ландау, И.Е. Тамма и т. д. И. В. Курчатов известен своими работами в области атомной физики. С. В. Королев осуществил первый космический полет. Известны и другие физики. Физические черты и характеристики свойственны любым явлениям природы, в том числе и тем, которые используются в различных отраслях техники, причем в этом случае приходится иметь дело со сложным комплексом явлений. Таким образом, физика служит естественной основой технических наук. Например, механика является основой таких дисциплин, как теоретическая механика, теория упругости и сопротивление материалов, используемых при проектировании станков, машин, автомобилей. Термодинамика развилась в разделы тепло - и хладотехники. Без знания вопросов электричества и магнетизма невозможно изучение таких наук, как электротехника, радиотехника, электроника, которые играют ведущую роль в развитии автоматики, телемеханики и телеуправления. Возрастающая роль физики в современной технике получила свое выражение в появлении ряда специальных дисциплин таких, как физические основы электротехники, физические основы резания металла и др. Все глубже в технику внедряются физические методы обработки и испытания материалов, физические методы контроля производственных процессов и качества изделий и т. п От современных инженеров требуется не только умело применять существующее оборудование, но и повсеместно развивать и совершенствовать технику. Такая творческая работа возможна только при хорошем знании физики. Вот почему хорошее усвоение физики необходимо инженеру. Большую роль играет физика и в формировании научного мировоззрения специалиста. Учебное пособие написано в соответствии с действующей программой курса физики для инженерно - технических специальностей высших учебных заведений и предназначено для студентов дневной, вечерней и заочной форм обучения с ограниченным числом часов по физике. Пособие состоит из двух частей. В первой части дано изложение физических основ классической механики и рассмотрены элементы специальной теории относительности. Вторая часть посвящена основам молекулярной физики и термодинамики. Сведения о размерностях физических величин и системных единиц вынесены в приложения.
КИНЕМАТИКА 1.1. Модели в механике. Система отсчета. Траектория, длина пути, вектор перемещения Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка - тело, обладающее массой, размером которого в данной задаче можно пренебречь. Понятие материальной точки абстрактное, но его введение облегчает решение практических задач. Например, изучая движение планет по орбитам вокруг Солнца, можно принять их за материальные точки. Произвольное макроскопическое тело или систему тел можно мысленно разбить на целые, взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек. В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек. Под воздействием тел друг на друга тела могут деформироваться, т.е. изменять свою форму и размеры. Поэтому в механике вводится еще одна модель - абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остается постоянным. Любое движение твердого тела можно представить как комбинацию поступательного и вращательного движений. Поступательное движение - это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение - это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение. Положение материальной точки определяется по
отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета. С ним связывается система отсчета - совокупность системы координат и часов, связанных с телом отсчета. В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент времени по Рис. 1 отношению к этой системе характеризуется тремя координатами х, у и z или радиусом-вектором В общем случае ее движение определяется скалярными уравнениями: х = x(t), y = y(t), (1.1) z = z(t), эквивалентными векторному уравнению
Уравнении (1.1), (1.2) называются кинематическими уравнениями движения материальной точки. Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы. Если материальная точка свободно движется в пространстве, то, как уже было сказано, она обладает тремя степенями свободы (координаты х, у, z); если она движется по некоторой поверхности, то - двумя степенями свободы; если вдоль некоторой линии, то - одной. Исключая t в уравнениях (1.1) и (1.2), получим уравнение траектории движения материальной точки. Траектория движения материальной точки - линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.
Вектор При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории, и модуль перемещения Скорость
Для характеристики движения материальной точки вводится векторная величина - скорость, которой определяется как быстрота движения, так и его направление в данный момент времени. Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор Вектором средней скорости
Направление вектора средней скорости совпадает с направлением
Так как секущая в пределе совпадает с касательной, то вектор скорости модуль мгновенной скорости
Таким образом, модуль мгновенной скорости равен первой производной пути по времени:
При неравномерном движении модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной <
Из рис.3 вытекает, что < Если выражение ds =
В случае равномерного движения числовое значение мгновенной скорости постоянно; тогда выражение (1.5) примет вид
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ Второй закон Ньютона Второй закон Ньютона - основной закон динамики поступательного движения - отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил. Если рассмотреть действие различных сил на одно и то же тело, то оказывается, что ускорение, приобретаемое телом, всегда прямо пропорционально равнодействующей приложенных сил: a~F (m=const). (2.1)
При действии одной и той же силы на тела с разными массами их ускорение оказывается различным, а именно: a~ Используя выражения (2.1) и (2.2) и учитывая, что сила и ускорение -величины векторные, можем записать
Соотношение (2.3) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). В СИ коэффициент пропорциональности k = 1. Тогда
или
Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (2.4) ее можно ввести под знак производной:
Векторная величина
Подставляя (2.6) в (2.5), получим
Это выражение – более общая формулировка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе. Выражение (2.7) называется уравнением движения материальной точки. Единица силы в СИ – ньютон (Н): 1 Н - сила, которая массе в 1кг сообщает ускорение 1 м/с2 в направлении действия силы: 1 Н = Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго. Действительно, в случае равенства нулю равнодействующей сил (при отсутствии воздействия на тело со стороны других тел) ускорение (см. (2.3)) также равно нулю. Однако первый закон Ньютона рассматривается как самостоятельный закон (а не как следствие второго закона), т. к. именно он утверждает существование инерциальных систем отсчета, в которых только и выполняется уравнение (2.7). В механике большое значение имеет принцип независимости действия сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. Согласно этому принципу, силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач. Например, на рис.10 действующая сила
Третий закон Ньютона Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:
где При использовании законов динамики иногда допускают следующую ошибку: т. к. действующая сила всегда вызывает равную по модулю и противоположную по направлению силу противодействия, то, следовательно, их равнодействующая должна быть равна нулю и тела вообще не могут приобрести ускорения. Однако надо помнить, что во втором законе Ньютона речь идет об ускорении, приобретаемом телом под действием приложенных к нему сил. Равенство нулю ускорения означает равенство нулю равнодействующей сил, приложенных к одному и тому же телу. Третий же закон Ньютона говорит о равенстве сил, приложенных к различным телам. На каждое из двух взаимодействующих тел действует только одна сила, которая и сообщает данному телу ускорение. Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.
Силы трения Обсуждая до сих пор силы, мы не интересовались их происхождением. Однако в механике мы будем рассматривать различные силы: трения, упругости, тяготения. Из опыта известно, что всякое тело, движущееся по горизонтальной поверхности другого тела, при отсутствии действия на него других сил с течением времени замедляет свое движение и в конце концов останавливается. Это можно объяснить существованием силы трения, которая препятствует скольжению соприкасающихся тел друг относительно друга. Силы трения зависят от относительных скоростей тел. Силы трения могут быть разной природы, но в результате их действия механическая энергия всегда превращается во внутреннюю энергию соприкасающихся тел. Различают внешнее (сухое) и внутреннее (жидкое или вязкое) трение. Внешним трением называется трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении. Обсудим некоторые закономерности внешнего трения. Это трение обусловлено шероховатостью соприкасающихся поверхностей; в случае же очень гладких поверхностей трение обусловлено силами межмолекулярного притяжения. Рассмотрим лежащее на поверхности тело (рис. 11), к которому приложена горизонтальная сила F.
сила трения скольжения F пропорциональна силе N нормального давления, с которой одно тело действует на другое:
где f - коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей.
Закон сохранения импульса. Центр масс
Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой или изолированной. Если мы имеем механическую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направлены, т.е. геометрическая сумма внутренних сил равна нулю. Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны
…………………..
Складывая почленно эти уравнения, получим
Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то
или
где Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему. В случае отсутствия внешних сил (рассматриваем замкнутую систему)
т.е.
Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени. Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т.е. закон сохранения импульса - фундаментальный закон природы. Закон сохранения импульса является следствием определенного свойства симметрии пространства - его однородности. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала координат инерциальной системы отсчета. Отметим, что, согласно (2.9), импульс сохраняется и для незамкнутой системы, если геометрическая сумма всех внешних сил равна нулю. В механике Галилея - Ньютона из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс. Центром масс или центром инерции системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Ее радиус - вектор равен
где mi и Скорость центра масс Учитывая, что
т.е. импульс системы равен произведению массы системы на скорость ее центра масс. Подставив выражение (2.10) в уравнение (2.9), получим
т.е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. Выражение (2.11) представляет собой закон движения центра масс. В соответствии с (2.10) из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным. РАБОТА И ЭНЕРГИЯ Энергия, работа, мощность Энергия - универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других - переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной последним телом. Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Если тело движется прямолинейно и на него действует постоянная сила
В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (3.1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение
где a - угол между векторами Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу
Для вычисления этого интеграла надо знать зависимость силы F от пути s вдоль траектории 1-2. Пусть эта зависимость представлена графически (рис.13), тогда искомая работа А определяется на графике площадью закрашенной фигуры. Если, например, тело движется прямолинейно, сила F=const, a=const, то получим
где s - пройденный телом путь (см. также формулу (3.1)). Из формулы (3.1) следует, что при Если Единица работы - джоуль (Дж): 1 Дж - работа, совершаемая силой в 1 Н на пути в 1 м (1 Дж = 1 Н-м). Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:
За время dt сила
т.е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N - величина скалярная. Единица мощности – ватт (Вт): 1 Вт - мощность, при которой за время 1с совершается работа в 1 Дж (1 Вт = 1 Дж/с).
Закон сохранения энергии Закон сохранения энергии - результат обобщения многих экспериментальных данных. Идея этого закона принадлежит М.В.Ломоносову (1711 - 1765 гг.), изложившему закон сохранения материи и движения, а количественная формулировка закона сохранения энергии дана немецким врачом Ю. Майером (1814 -1878 гг.) и немецким естествоиспытателем Г. Гельмгольцем (1821 - 1894 гг.). Рассмотрим систему материальных точек массами m1, m2, …, mn, движущихся со скоростями Ньютона для этих точек следующие:
……………………..
Двигаясь под действием сил, точки системы за интервал времени dt совершают перемещения, соответственно равные
…………………………………
Сложив эти уравнения, получим
Первый член левой части равенства (3.11)
где dT есть приращение кинетической энергии системы. Второй член Правая часть равенства (3.11) задает работу внешних неконсервативных сил, действующих на систему. Таким образом, имеем d(T+П)=dA. (3.12) При переходе системы из состояния 1 в какое-либо состояние 2
т.е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними нек
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.21.101 (0.011 с.) |

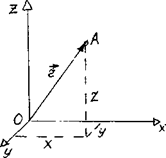
 , проведенным из начала системы координат в данную точку (рис.1) При движении материальной точки ее координаты с течением времени изменяются.
, проведенным из начала системы координат в данную точку (рис.1) При движении материальной точки ее координаты с течением времени изменяются. (1.2)
(1.2) Рис. 2
Рис. 2
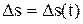 .
.
 ,проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением.
,проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением. равен пройденному пути
равен пройденному пути  s.
s.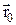 (рис.3). В течение малого промежутка времени Δt точка пройдет путь ΔS получит элементарное (бесконечно малое) перемещение
(рис.3). В течение малого промежутка времени Δt точка пройдет путь ΔS получит элементарное (бесконечно малое) перемещение  .
. называется отношение приращения
называется отношение приращения  . (1.3).
. (1.3). :
: .
. Рис. 3
Рис. 3
 .
. . (1.4)
. (1.4) >- средней скоростью неравномерного движения:
>- средней скоростью неравномерного движения: .
. , так как s>
, так как s> 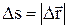 .
. (1.5)
(1.5)
 (F=const). (2.2)
(F=const). (2.2)
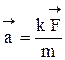 (2.3)
(2.3)
 . (2.4)
. (2.4) . (2.5)
. (2.5) , (2.6)
, (2.6) . (2.7)
. (2.7) .
. разложена на два компонента: тангенциальную силу
разложена на два компонента: тангенциальную силу  (направлена по касательной к траектории) и нормальную силу
(направлена по касательной к траектории) и нормальную силу  (направлена по нормали к центру кривизны). Используя выражения
(направлена по нормали к центру кривизны). Используя выражения  и
и  , а также
, а также 


 (2.8)
(2.8) - сила, действующая на первую материальную точку со стороны второй;
- сила, действующая на первую материальную точку со стороны второй;  - сила, действующая на вторую материальную точку со
- сила, действующая на вторую материальную точку со Рис. 11
Рис. 11
 ,
, и
и  ,
,  ,…,
,…,  . Пусть
. Пусть  - равнодействующие внутренних сил, действующих на каждое из этих тел, а
- равнодействующие внутренних сил, действующих на каждое из этих тел, а  - равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:
- равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:




 (2.9)
(2.9) - импульс системы.
- импульс системы.


 - соответственно масса и радиус-вектор i -и материальной точки; n - число материальных точек в системе;
- соответственно масса и радиус-вектор i -и материальной точки; n - число материальных точек в системе;  - масса системы.
- масса системы.
 , a
, a  есть импульс
есть импульс  системы, можно
системы, можно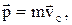 (2.10)
(2.10) (2.11)
(2.11) , которая составляет некоторый угол a с направлением перемещения, то работа этой силы равна произведению проекции силы
, которая составляет некоторый угол a с направлением перемещения, то работа этой силы равна произведению проекции силы  на направление перемещения
на направление перемещения  умноженной на перемещение точки приложения силы:
умноженной на перемещение точки приложения силы: . (3.1)
. (3.1) , то силу
, то силу 
 - элементарный путь; Fs - проекция вектора
- элементарный путь; Fs - проекция вектора  (3.2)
(3.2)

 <
<  работа силы положительна, в этом случае составляющая Fs совпадает по направлению с вектором скорости движения v (рис.12).
работа силы положительна, в этом случае составляющая Fs совпадает по направлению с вектором скорости движения v (рис.12). (3.3)
(3.3) , и мощность, развиваемая
, и мощность, развиваемая ,
, . Пусть
. Пусть  – равнодействующие внутренних консервативных сил, действующих на каждую из этих точек, а
– равнодействующие внутренних консервативных сил, действующих на каждую из этих точек, а  – равнодействующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначим
– равнодействующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначим  . При
. При


 . Умножим каждое из уравнений скалярно на соответствующее перемещение и, учитывая, что
. Умножим каждое из уравнений скалярно на соответствующее перемещение и, учитывая, что  , получим:
, получим:

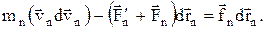
 (3.11)
(3.11)
 равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т.е. равен элементарному приращению потенциальной энергии dП системы (3.5).
равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т.е. равен элементарному приращению потенциальной энергии dП системы (3.5). ,
,


