
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И одинаковой частоты. БиенияСодержание книги
Поиск на нашем сайте
Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты
воспользовавшись методом вращающегося вектора амплитуды. Построим векторные диаграммы этих колебаний (рис. 29). Так как векторы A1 и A2 вращаются с одинаковой угловой скоростью wо, то разность фаз (j2-j1)
между ними остается постоянной. Очевидно, что уравнение результирующего колебания будет:
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармонические колебания в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз Проанализируем выражение (5.22) в зависимости от разности фаз 1) 2) Для практики особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. В результате сложения этих двух колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебаний, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями. Пусть амплитуды складываемых колебаний равны А, а частоты равны w и w+Dw причем Dw<w. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:
Складывая эти выражения и учитывая, что во втором сомножителе
Получившееся выражение есть произведение двух колебаний. Так как
Частота изменения Аб в два раза больше частоты изменения косинуса
Определение частоты тона биений между эталонным и измеряемым колебаниями - наиболее широко применяемый на практике метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т. д.
|
||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.20.205 (0.009 с.) |

 ,
,
 . (5.21)
. (5.21) Рис. 29
Рис. 29
 ,
,
 . (5.22)
. (5.22)
 складываемых колебаний.
складываемых колебаний. , тогда А=А1+А2, т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;
, тогда А=А1+А2, т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний; , тогда
, тогда  , т.е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
, т.е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
 , найдем
, найдем . (5.23)
. (5.23)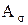 которого изменяется по следующему периодическому закону:
которого изменяется по следующему периодическому закону: . (5.24)
. (5.24) . Характер зависимости (5.23) показан на рис. 30, где сплошные жирные линии дают график результирующего колебания (5.23), а огибающие их - график медленно меняющейся по уравнению (5.24) амплитуды.
. Характер зависимости (5.23) показан на рис. 30, где сплошные жирные линии дают график результирующего колебания (5.23), а огибающие их - график медленно меняющейся по уравнению (5.24) амплитуды.



