
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Амплитуда и фаза вынужденных колебаний. РезонансСодержание книги
Поиск на нашем сайте
Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты w. Чтобы определить резонансную частоту
Это равенство выполняется при
Явление резкого возрастания амплитуды вынужденных колебаний при Подставляя (5.44) в формулу (5.42), получим
На рис. 36 приведена зависимость амплитуды колебаний от частоты при различных δ. Из (5.44) и (5.45) вытекает что, чем меньше δ, тем выше и правее лежит максимум данной кривой. Если w®0, то все кривые приходят к одному и тому же, отличному от нуля, предельному значению
Из формулы (5.46) вытекает, что при малом затухании
где Q - добротность колебательной системы (5.35), Зависимость
При дальнейшем увеличении w сдвиг фаз возрастает и при Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы их собственная частота колебаний не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора. Так, радиотехника, прикладная акустика, электротехника используют явление резонанса.
ЭЛЕМЕНТЫ МЕХАНИКИ ЖИДКОСТЕЙ
Давление в жидкости и газе
Молекулы газа, совершая беспорядочное, хаотическое движение, не связаны или весьма слабо связаны силами взаимодействия, поэтому они движутся свободно и в результате соударения стремятся разлететься во все стороны, заполняя весь предоставленный им объем. Как и газ, жидкость принимает форму того сосуда, в который она заключена. Но в жидкостях в отличие от газов среднее расстояние между молекулами остается практически постоянным, поэтому жидкость обладает практически неизменным объемом. Хотя свойства жидкостей и газов во многом отличаются, в ряде механических явлений их поведение определяется одинаковыми параметрами и идентичными уравнениями. Поэтому гидроаэромеханика - раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и обтекаемыми ими твердыми телами, - использует единый подход к изучению жидкостей и газов. В механике с большой степенью точности жидкости и газы рассматри-ваются как сплошные, непрерывно распределенные в занятой ими части пространства. Плотность жидкости мало зависит от давления. Плотность же газов от давления зависит существенно. Из опыта известно, что сжимаемостью жидкости и газа во многих задачах можно пренебречь и пользоваться единым понятием несжимаемой жидкости - жидкости, плотность которой всюду одинакова и не изменяется со временем. Если в покоящуюся жидкость поместить тонкую пластинку, то части жидкости, находящиеся по разные стороны от нее, будут действовать на каждый ее элемент DS с силами DF, которые, независимо от того как пластинка ориентирована, будут равны по модулю и направлены перпендикулярно площадке DS, т.к. наличие касательных сил привело бы частицы жидкости в движение. Физическая величина, определяемая нормальной силой, действующей со стороны жидкости на единицу площади, называется давлением р жидкости:
Единица давления – паскаль (Па): 1 Па равен давлению, создаваемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1м2 (1 Па=1 Н/м2). Давление при равновесии жидкостей (газов) подчиняется закону Паскаля: давление в любом месте покоящейся жидкости одинаково по всем направлениям, причем давление одинаково передается по всему объему, занятому покоящейся жидкостью. Рассмотрим, как влияет вес жидкости на распределение давления внутри покоящейся несжимаемой жидкости. При равновесии жидкости давление по горизонтали всегда одинаково, иначе не было бы равновесия. Поэтому свободная поверхность покоящейся жидкости всегда горизонтальна вдали от стенок сосуда. Если жидкость несжимаема, то ее плотность не зависит от давления. Тогда при поперечном сечении S столба жидкости, его высоте h и плотности rвес Р=rgSh, а давление на нижнее основание Сила давления на нижние слои жидкости будет больше, чем на верхние, поэтому на тело, погруженное в жидкость, действует выталкивающая сила, определяемая законом Архимеда: на тело, погруженное в жидкость (газ), действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости (газа):
Уравнение неразрывности
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости – потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводят так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 38). Линии тока проводят так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т.е. можно определить состояние движения жидкости. Линии тока в жидкости можно "проявить", например, подмешав в нее какое-либо заметные взвешенные частицы.
Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются. Рассмотрим какую-либо трубку тока. Выберем два ее сечения S1 и S2, перпендикулярные направлению скорости (рис. 39). За время Dt через сечение S проходит объем жидкости S
Следовательно, произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение (6.1) называется уравнением неразрывности для несжимаемой жидкости.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.145.41 (0.007 с.) |

 - частоту, при которой амплитуда А смещения достигает максимума, - нужно найти максимум функции или, что то же самое, минимум подкоренного выражения. Продифференцировав подкоренное выражение по w и приравняв к нулю, получим условие, определяющее
- частоту, при которой амплитуда А смещения достигает максимума, - нужно найти максимум функции или, что то же самое, минимум подкоренного выражения. Продифференцировав подкоренное выражение по w и приравняв к нулю, получим условие, определяющее  .
. , у которого только
, у которого только . (5.44)
. (5.44) <<
<<  значение
значение  . (5.45)
. (5.45) так называемому статическому отклонению.
так называемому статическому отклонению. Рис. 36
Рис. 36
 . Если w®¥, то все кривые асимптотически стремятся к нулю. Приведенные на рис. 36 кривые называются резонансными кривыми.
. Если w®¥, то все кривые асимптотически стремятся к нулю. Приведенные на рис. 36 кривые называются резонансными кривыми.
 , (5.46)
, (5.46) - статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше
- статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше  .
. от w при разных коэффициентах d графически представлена на рис.37, из которого следует, что при изменении w изменяется и сдвиг фаз j.
от w при разных коэффициентах d графически представлена на рис.37, из которого следует, что при изменении w изменяется и сдвиг фаз j.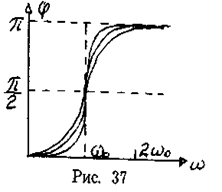
 вытекает, что при w=0 j=0, а при w=w0 независимо от значения коэффициента затухания
вытекает, что при w=0 j=0, а при w=w0 независимо от значения коэффициента затухания 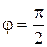 , т.е. вынуждающая сила опережает вынуждающие по фазе колебания на
, т.е. вынуждающая сила опережает вынуждающие по фазе колебания на  .
.
 >>w0
>>w0  , т.е. фаза колебаний почти противоположна фазе внешней силы. Семейство кривых, изображенных на рис. 37, называется фазовыми резонансными кривыми.
, т.е. фаза колебаний почти противоположна фазе внешней силы. Семейство кривых, изображенных на рис. 37, называется фазовыми резонансными кривыми. .
.
 , т.е. давление изменяется линейно с высотой. Давление
, т.е. давление изменяется линейно с высотой. Давление 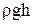 называется гидростатичес-ким давлением.
называется гидростатичес-ким давлением. , где r - плотность жид-кости, V - объем погруженного в жидкость тела.
, где r - плотность жид-кости, V - объем погруженного в жидкость тела.
 t; следовательно, за 1 с через S1 пройдет объем жидкости S1
t; следовательно, за 1 с через S1 пройдет объем жидкости S1  , где
, где  , где
, где  - скорость течения жидкости в месте сечения S2. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема, то через сечение S1пройдет такой же объем жидкости, как и через сечение S2) т.е.
- скорость течения жидкости в месте сечения S2. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема, то через сечение S1пройдет такой же объем жидкости, как и через сечение S2) т.е. . (6.1)
. (6.1)


