
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подставляя (7.10) в (7.9), получимСодержание книги
Поиск на нашем сайте
или Из соотношения (7.10) вытекает, что t<t', т.е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Этот результат может быть еще истолкован следующим образом: интервал времени t', отсчитанный по часам в системе К', с точки зрения наблюдателя в системе К, продолжительнее интервала t, отсчитанного по его часам. Следовательно, часы, движущиеся относительно инерциальной системы отсчета идут медленнее покоящихся часов. На основании относительности понятий "неподвижная" и "движущаяся" системы соотношения для t и t' обратимы. Из (7.11) следует, что замедление хода часов становится заметным лишь при скоростях, близких к скорости света в вакууме. Релятивистский эффект замедления хода часов является совершенно реальным и получил экспериментальное подтверждение при изучении нестабильных, самопроизвольно распадающихся элементарных частиц в опытах с p-мезонами. Среднее время жизни покоящихся p-мезонов (по часам, движущимся вместе с ними) t»2,2×10-8 с. Следовательно, p-мезоны, образующиеся в верхних слояхатмосферы(на высоте» 30 км) и движущиеся со скоростью, близкой кскорости света, должны были бы проходить расстояние ст=6,6 м, т.е. не могли бы достигать земной поверхности, что противоречит действительности.
3. Длина тел в разных системах отсчета. Рассмотрим стержень, расположенный вдоль оси х' и покоящийся относительно системы К'. Длина стержня в системе К' будет Используя преобразования Лоренца (7.8), получим
т.е. Таким образом, длина стержня, измеренная в системе, относительно которой он движется, оказывается меньше длины, измеренной в системе, относительно которой стержень покоится. Если стержень покоится в системе К, то, определяя ее длину в системе К, опять-таки придем к выражению (7.12). Из выражения (7.12) следует, что линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения в
4. Релятивистский закон сложения скоростей. Рассмотрим движение материальной точки в системе К', в свою очередь движущейся относительно системы К со скоростью
и представляет собой соответственно проекции на оси х, у, zи х', у', z' вектора скорости рассматриваемой точки относительно систем К и К'. Согласно преобразованиям Лоренца (7.8), произведя соответствующие преобразования, получаем релятивистский закон сложения скоростей специальной теории относительности:
Если материальная точка движется параллельно относительно осих, то скорость и относительно системы К совпадает с ux, а скорость u' относительно К'- сu'x. Тогда закон сложения скоростей примет вид
Легко убедиться в том, что, если скорости Релятивистский закон сложения скоростей подчиняется второму постулату Эйнштейна. Действительно, если u'=с, то формула (7.14) примет вид Докажем также, что если складываемые скорости сколь угодно близки к скорости света с, тоих результирующая скорость будет всегда меньше или равна с. В качестве примера рассмотрим предельный случай u'=
Интервал между событиями Преобразования Лоренца и следствия из них приводят к выводуоботносительности длин и промежутков времени, значение которых вразличных системах отсчета разное. В то же время относительный характер длин и промежутков времени в теории Эйнштейна означает относительность отдельных компонентов какой-то реальной физической величины, не зависящей от системы отсчета, т.е. являющейся инвариантной по отношению к преобразованиям координат. В четырехмерном пространстве Эйнштейна, в котором каждое событие характеризуется четырьмя координатами (х,у, z, t), такой физической величиной является интервал между двумя событиями:
где,
Покажем, что интервал между двумя событиями одинаков вовсех инерциальных системах отсчета. Обозначив Dt=t2 –t1, выражение (7.15) можно записать в виде
Интервал между теми же событиями в системе К' равен
Согласно преобразованиям Лоренца (7.8),
Подставив эти значения в (7.16), после элементарных преобразований получим, что Обобщая полученные результаты, можно сделать вывод, что интервал, определяя пространственно-временные соотношения между событиями, является инвариантом при переходе от одной инерциальной системы отсчета к другой. Инвариантность интервала означает, что, несмотря на относительность длин и промежутков времени, течение событий носит объективный характер и не зависит от системы отсчета. Теория относительности, таким образом, сформулировала новое представление о пространстве и времени, обобщенное далее в диалектическом материализме. Пространственно-временные отношения являются не абсолютными величинами, как утверждала механика Галилея-Ньютона, а относительными. Следовательно, представления об абсолютном пространстве и времени являются несостоятельными. Кроме того, инвариантность интервала между двумя событиями свидетельствует о том, что пространство и время органически связаны между собой и образуют единую форму существования материи – пространство – время. Пространство и время не существуют вне материи и независимо от нее. Дальнейшее развитие относительности (общая теория относительности) показало, что свойства пространства-времени в данной области определяются действующими в ней полями тяготения.
|
||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.111 (0.007 с.) |


 . (7.11)
. (7.11) =x2'-x1', где x1' и x2' - не изменяющиеся со временем t' координаты начала и конца стержня, а индекс 0 показывает, что в системе отсчета К' стержень покоится. Определим длину этого стержня в системе К, относительно которой он движется со скоростью
=x2'-x1', где x1' и x2' - не изменяющиеся со временем t' координаты начала и конца стержня, а индекс 0 показывает, что в системе отсчета К' стержень покоится. Определим длину этого стержня в системе К, относительно которой он движется со скоростью  . Для этого необходимо измерить координаты его концов х1 и х2 в системе К в один и тот же момент времени t. Их разность
. Для этого необходимо измерить координаты его концов х1 и х2 в системе К в один и тот же момент времени t. Их разность  =х2 - х1 и даст длину стержня в системе К.
=х2 - х1 и даст длину стержня в системе К. ,
, . (7.12)
. (7.12) раз, т.е. так называемое лоренцово сокращение длины тем больше, чем больше скорость движения. Из второго и третьего уравнений преобразования Лоренца (7.8) следует, что y'2-y’1=y2-y1 и z¢2 -z¢1=z2-z1, т.е. поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета. Таким образом, линейные размеры тела наибольшие в той инерциальной системе отсчета, относительно которой тело покоится.
раз, т.е. так называемое лоренцово сокращение длины тем больше, чем больше скорость движения. Из второго и третьего уравнений преобразования Лоренца (7.8) следует, что y'2-y’1=y2-y1 и z¢2 -z¢1=z2-z1, т.е. поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета. Таким образом, линейные размеры тела наибольшие в той инерциальной системе отсчета, относительно которой тело покоится.




 .
.


 (7.13)
(7.13)
 (7.14)
(7.14) =с (аналогично можно показать, что при u=с скорость u' также равна с). Этот результат свидетельствует в том, что релятивистский закон сложения скоростей находится в согласии с постулатами Эйнштейна.
=с (аналогично можно показать, что при u=с скорость u' также равна с). Этот результат свидетельствует в том, что релятивистский закон сложения скоростей находится в согласии с постулатами Эйнштейна.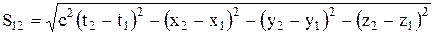 , (7.15)
, (7.15) - расстояние между точками обычного трехмерного пространства, в которомэти события произошли. Введя обозначение t12 =t2 –t1, получим
- расстояние между точками обычного трехмерного пространства, в которомэти события произошли. Введя обозначение t12 =t2 –t1, получим .
.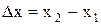 ,
, 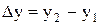 ,
,  ,
, .
. . (7.16)
. (7.16)
 , т.е. (S'12)=S12
, т.е. (S'12)=S12


