Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности вращательного движения.Содержание книги Поиск на нашем сайте Вопрос 14. Особенности вращательного движения.
Рассмотрим движение твердого тела, имеющею ось вращения O1O2 под действием произвольно направленной силы F, приложенной к телу в некоторой точке А, которую можно разложить на две составляющие: вертикальную и горизонтальную (рис.5.1). Вертикальная составляющая может вызывать перемещение тела в направлении оси вращения поэтому при рассмотрении вращательного движения ее можно исключить, как.Горизонтальная составляющая Fr, если она не пересекается с осью O1O2 вызывает вращение тела. Действие этой силы зависит от ее числового значения и расстояния линии действия от оси вращения. Момент силы. Пусть на тело, в плоскости перпендикулярной оси вращения O1O2 действует сила F (рис.5.2). Разложим эту силу на две составляющие: Fn и Fe
Сила Fn пересекает ось вращения и, следовательно, не влияет на вращение тела. Под действием составляющей Fe тело будет совершать вращательное движение вокруг оси O1O2. Расстояние r от оси вращения до линии, вдоль которой действует сила Fe, называется плечом силы Fe. Моментом силы относительно точки О называется произведение модуля силы Fx на плечо r: M=Fer. С учетом, что Fx=Fsina, => момент силы M=rFsina. С точки зрения векторной алгебры это выражение представляет векторное произведение радиуса-вектора r, проведенного в точку приложения силы F на эту силу. Таким образом, момент силы относительно точки О является векторной величиной и равен M=[r,F]. Вектор момента силы направлен перпендикулярно к плоскости, проведенной через векторы r и F, и образует с ними правую тройку векторов (при наблюдении из вершины вектора М видно, что вращение по кратчайшему расстоянию от r к F происходит против часовой стрелки). Момент инерции. Согласно второму закону Ньютона, для тангенциальной составляющей силы Fix, действующей на материальную точку массой m, и ускорения aix можем записать: Fix=miaix. С учетом, что Fix=Fisina и aix=riƐ, Имеем Fisina=miriƐ. Домножим левую и правую части на ri и получим: riFisina= miri2Ɛ, Или Mi== miri2Ɛ. Произведение массы материальной точки m1 тела на квадрат ее расстояния ri2 до оси вращения называется моментом инерции материальной точки относительно оси вращения: Ji=miri2. Теорема Штейнера. Момент инерции тела J любой оси вращения равен моменту его инерции J0 относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы m тела на квадрат расстояния a между ними J=J0+ma2. Закон Ньютона. Вращающий момент тела: M=JƐ. Это выражение представляет собой аналог второго закона Ньютона для вращательного движения, из которого следует, что угловое ускорение Ɛ твердого тела при вращении вокруг неподвижной оси прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции Относительно этой оси. Из этого выражения следует, что момент инерции U является мерой его инертности во вращательном движении вокруг неподвижной оси. В случае поступательного движения мерой инертности, как известно, является масса тела. Вопрос 15. Момент импульса. Векторное произведение радиуса-вектора ri материальной точки на ее импульс: mivi называют моментом импульса Li, этой точки относительно точки О (рис.5.4)
Li=[ri,mi,vi]. Вектор Li иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы ri и mivi и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от ri к mivi происходит против часовой стрелки). Векторную сумму моментов импульсов Li всех материальных точек системы называют моментом импульса (количества движения) L системы относительно точки О:
Векторы ri и mivi взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому Li= rimivisina= rimivi. С учетом связи линейных и угловых величин Li=miri2ω, и направлен вдоль оси вращения тела в ту же сторону, что и вектор ω. Таким образом. Li=miri2ω=Ji ω. Момент импульса тела относительно оси вращения
Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси. Закон сохранения импульса. Выясним, как изменяются импульсы двух тел при их взаимодействии. Обозначим скорости тел массами m1 и m2 до взаимодействия через V1 и V2, а после взаимодействия — через V1’ и V2’. По третьему закону Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению; поэтому их можно обозначить F и -F. Для изменений импульсов тел при их взаимодействии на основании равенства (16.2) можно записать: Ft=m1v1’- m1v1 и –Ft=m2v2’-m2v2, где t — время взаимодействия тел. Из этих выражений получаем: m1v1+m2v2=m1v1’+m2v2’ Таким образом, векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия.
Вопрос 16. Вопрос 17. Относительное движение
Относительное движение, движение точки (или тела) по отношению к подвижной системе отсчёта перемещающейся определённым образом относительно некоторой другой, основной системы отсчёта, условно наз. неподвижной. Вопрос 18. Вопрос 19. Преобразования Галлилея.
Дифференцируя эти уравнения по времени и учитывая, что u=const, найдем соотношения между скоростями и ускорениями: vx=vx’+u; ax=ax’; vz=vz’; ay=ay’; ay=ay’; vy=vy’; az=az’. Таким образом, если в системе К тело имеет ускорение а, то такое же ускорение оно имеет и в системе К’. Согласно второму закону Ньютона: F=ma, т.е. второй закон Ньютона одинаков в обоих случаях. При a=a’=0 движение по инерции, т.о., справедлив и первый закон Ньютона, т.е. рассматриваемая нами подвижная система является инерциальной. Следовательно, уравнения Ньютона для материальной точки, а также для произвольной системы материальных точек одинаковы во всех инерциальных системах отсчета - инвариантны по отношению к преобразованиям Галилея. Этот результат называется механическим принципом относительности (принцип относительности Галилея), и формулируется следующим образом: равномерное и прямолинейное движение (относительно какой-либо инерциальной системы отсчета) замкнутой системы не влияет на закономерности протекания в ней механических процессов. Следовательно, в механике все инерциальные системы отсчета совершенно равноправны. Поэтому никакими механическими опытами внутри системы нельзя обнаружить движется ли система равномерно и прямолинейно или покоится. Вопрос 20. Постулаты Эйнштейна. 1 постулат Эйнштейна или принцип относительности: все законы природы инвариантны по отношению ко всем инерциальным системам отсчета. Все физические, химические, биологические явления протекают во всех инерциальных системах отсчета одинаково. 2 постулат или принцип постоянства скорости света: скорость света в вакууме постоянна и одинакова по отношении» к любым инерциальным системам отсчета. Она не зависит ни от скорости источника света, ни от скорости его приемника. Ни один материальный объект не может двигаться со скоростью, превышающей скорость света в вакууме. Более того, пи одна частица вещества, т.е. частица с массой покоя, отличной от нуля, не может достичь скорости света в вакууме, с такой скоростью могут двигаться лишь полевые частицы, т.е. частицы с массой покоя, равной нулю. Анализируя 1 постулат Эйнштейна, мы видим, что Эйнштейн расширил рамки принципа относительности Галилея, распространив его на любые физические явления, в том числе и на электромагнитные. 1 постулат Эйнштейна непосредственно вытекает из опыта Майкельсона-Морли, доказавшего отсутствие в природе абсолютной системы отсчета. Из результатов этого нее опыта следует и 2 постулат Эйнштейна о постоянстве скорости света в вакууме, который тем не менее вступает в противоречие с 1 постулатом, если распространить на электромагнитные явления не только сам принцип относительности Галилея, но и галилеево правило сложения скоростей, вытекающее из правила Галлилея преобразования координат (см. п. 10). Следовательно, преобразования Галилея для координат и времени, а также его правило сложения скоростей к электромагнитным явлениям неприменимы. Преобразования Лоренца. Исходя из сформулированных выше постулатов теории относительности Эйнштейна, можно найти законы преобразований, связывающие межу собой пространственные координаты и время в двух системах отсчета, движущихся прямолинейно и равномерно относительно друг друга.
Пусть х, у, z, и х’, у’, z’ и t’,- координаты и время в инерциальных систем отсчета K и K’, а v - скорость их относительного движения (рис. 6.1). При этом нет никаких оснований полагать, что время в системе K’ совпадает со временем в системе K, как это безоговорочно принималось в классической физике. Для просторы выкладок выберем направление скорости за направление осей х и x’. Предположим, что в некоторый момент времени t’ в точке скоординатами x’,y’,z’происходит некоторый физический процесс, который назовем событием. Нашей задачей является нахождение «координат» события в системе отсчета K’, т.е. нахождение величин х, y, z, t, характеризующих тот же физический процесс в системе K.
Выберем за начало отсчета времени t=0 тот момент, в который начало координат системы K’ совпадало с началом координат системы K. Пусть в момент времени t=0 из начала координат начала распространяться сферическая электромагнитная волна (рис.6.2). В системе K уравнение волновой поверхности имеет вид. x2+y2+z2=c2t2 или x2+y2+z2-c2t2=0 Поскольку, согласно принципу относительности Эйнштейна, закон и величина скорости распространения волны должны быть одинаковыми во всех инерциальных системах отсчета, наряду с этим уравнением с равным правом можно написать уравнение сферической волны в системе K’.(x’)2+(y’)2+(z’)2-c2(t’)2=0. Так как в начальный момент времени начало координат систем совпадали, то x’2+y’2+z’2-c2t’2=x2+y2+z2-c2t2. Формулы преобразования координат и времени должны, во-первых, не нарушать соотношений (6.1) и (6.2), а, во-вторых, быть линейными. Требования линейности связано с однородностью пространства. Т.к. движение системы K’ происходит только вдоль оси х преобразование координат у и z должно иметь вид y’=y, z’=z. Закон преобразования х’ через х можно написать, исходя из следующегосоображения: если в момент времени t=0 начала систем координат K и K’ совпадали, то координата плоскости х’ в системе K запишется х=νt. Следовательно, в самом общем случае можно написать x’=a(v)(x-vt), где коэффициент a(v) может зависеть лишь от скорости относительного движения. Не делая никаких произвольных допущений о совпадении времени в двух системах отсчета, мы можем представить t’ в виде линейной однородной функции х и t: t’=βt+yx. Kоэффициенты β и y могут, вообще говоря, зависеть от скорости v. Если бы оказалось, что y=0, а β=1, то мы вернулись бы к преобразованиям Галилея. Для определения коэффициентов a, β и y, отвечающих Требованиям принципа относительности Эйнштейна, мы должны подставить (6.3) и (6.5) в (6.2). Это дает a2(x-vt)2+y2+z2-c2(βt+yx)2=x2+y2+z2-c2t2. Для выполнения тождества необходимо приравнять коэффициенты при х2,t2и хt. Раскрыв скобки и проведя соответствующие преобразования получим: a2-c2y2=1; a2v2-c2β2=-c2;; a2v2-c2β2y=0 Из этих трех уравнений находим неизвестные величины a, β и y,:
При этом всюду мы выбрали положительный знак корня. Подставляя значения
Эти формулы носят название преобразований Лоренца. Формулы обратного преобразования от штрихованных к не штрихованным величинам:
Преобразования Лоренца приводят к выводам, коренным образом противоречащим привычным представлениям о свойствах времени и пространства, сложившимся на основе повседневного опыта. Рассмотрим несколько примеров применения преобразований Лоренца.
Вопрос 21. Вопрос 22. Следствия из преобразований Лоренца 1. Если в одной системе отсчета некоторые события происходят в точках x 1 и x 2 в один и тот же момент вр емени t, то в другой системе отсчета эти события происходят в точках x '1 и x '2 в разные моменты времени t '1 и t '2: t1’-t2’=u(x2’-x1’)/c2 Понятие одновременности оказывается зависящим от выбора системы отсчета. 2. Если в одной системе отсчета между двумя событиями, происходящими в одной и той же точке, проходит время t, то в другой системе отсче та между этими же событиями проходит время
Это соотношение выражает релятивистский эффект замедления времени в движущихся объектах. 3. Если в одной системе отсчета покоящаяся линейка имеет длину l, то в системе отсчета, в которой линейка движется со скоростью u вдоль своей оси, ее длина
Этот эффект называется релятивистским сокращением продольных размеров тела. Поперечные размеры тела не изменяются при переходе в другие инерциа льные системы отсчета. 4. Если в одной системе отсчета тело имеет скорость v = (vx, vy, vz), то его скорос ть v ' = (v'x, v'y, v'z) в другой системе отсчета равна
или в трехмерной векторной форме 5. Из соотношени (n4), (n5) следует постоянство скорости c в различных системах отсчета. Действительно, если вычислить сумму квадратов левых частей этих равенств при условии v 2=(vx)2+(vy) 2+(vz) 2= c 2, (n6) получим v' 2=(v'x)2+ (v'y)2+(v'z) 2= c 2. (n7) Т. е. скорость c одинакова по величине во всех инерциальных системах отсчета (независимо от направления). Заметим, что направления скоростей v и v ' в общем случае различны в разных системах отсчета. Лоренцево сокращение длины
Пусть l0 = x'2 – x'2 – собственная длина тела в системе, относительно которого тело неподвижно (например: в ракете, движущейся со скоростью мимо неподвижной системы отсчета k (Земля)). Измерение координат x1 и x2 производим одновременно в системе k, т.е. t1 = t2 = t. Используя преобразования Лоренца, для координат получим:
Тогда
Формулы (8.4.6) описывают лоренцево сокращение длин. Собственная длина тела есть максимальная длина. Длина движущегося тела короче, чем покоящегося. Причем сокращается только проекция на ось x, т.е. размер тела вдоль направления движения. Вопрос 23. Следствия из преобразований Лоренца 1. Если в одной системе отсчета некоторые события происходят в точках x 1 и x 2 в один и тот же момент вр емени t, то в другой системе отсчета эти события происходят в точках x '1 и x '2 в разные моменты времени t '1 и t '2: t1’-t2’=u(x2’-x1’)/c2 (n1) Понятие одновременности оказывается зависящим от выбора системы отсчета. 2. Если в одной системе отсчета между двумя событиями, происходящими в одной и той же точке, проходит время t, то в другой системе отсче та между этими же событиями проходит время
Это соотношение выражает релятивистский эффект замедления времени в движущихся объектах. 3. Если в одной системе отсчета покоящаяся линейка имеет длину l, то в системе отсчета, в которой линейка движется со скоростью u вдоль своей оси, ее длина
Этот эффект называется релятивистским сокращением продольных размеров тела. Поперечные размеры тела не изменяются при переходе в другие инерциа льные системы отсчета. 4. Если в одной системе отсчета тело имеет скорость v = (vx, vy, vz), то его скорос ть v ' = (v'x, v'y, v'z) в другой системе отсчета равна
или в трехмерной векторной форме 5. Из соотношени (n4), (n5) следует постоянство скорости c в различных системах отсчета. Действительно, если вычислить сумму квадратов левых частей этих равенств при условии v 2=(vx)2+(vy) 2+(vz) 2= c 2, (n6) получим v' 2=(v'x)2+ (v'y)2+(v'z) 2= c 2. (n7) Т. е. скорость c одинакова по величине во всех инерциальных системах отсчета (независимо от направления). Заметим, что направления скоростей v и v ' в общем случае различны в разных системах отсчета. Замедление времени Пусть вспышка лампы на ракете длится τ = t'2 – t'1, где τ – собственное время, измеренное наблюдателем, движущимся вместе с часами. Чему равна длительность вспышки (t2 – t1) с точки зрения человека, находящегося на Земле, мимо которого пролетает ракета? Так как x'1 = x'2 то из преобразований Лоренца
Из этого уравнения следует, что собственное время – минимально (движущиеся часы идут медленнее покоящихся). Таким образом, вспышка на Земле будет казаться длиннее. Этот вывод имеет множество экспериментальных подтверждений. Так, нестабильные элементарные частицы – пионы, рождающиеся в верхних слоях атмосферы, на высоте 20–30 км, при воздействии на нее космических лучей имеют собственное время жизни τ ~ 2·10-6 с. За это время они могут пройти короткий путь S = c·τ = 600 м. Но в результате того, что они двигаются с очень большими скоростями, сравнимыми со скоростью света, их время жизни увеличивается и они до своего распада способны достигать поверхности Земли. Отсюда следует вывод, что у движущихся пионов секунды «длиннее» земных секунд. В 70-е г. замедление времени наблюдалось не только с помощью нестабильных микрочастиц, но и проводились прямые измерения с использованием высокоточных часов, основанных на эффекте Мессбауэра. Двое таких часов показывают одно и то же время с точностью до 10-16 с. В 1971 г. Хафель и Китинг осуществили прямое измерение замедления времени, отправив два экземпляра атомных часов в кругосветное путешествие на реактивном самолете. Потом их показания сравнили с показаниями таких же часов, оставленных на Земле, в лаборатории ВМС США. Время запаздывания составило 273·10-9 с, что в пределах ошибок согласуется с теорией. Это следствие из преобразований Лоренца объясняет известный всем «парадокс близнецов».
Вопрос 24. Релятивистский импульс. Уравнения классической механики инвариантны по отношению к преобразованиям Галилея, по отношению же к преобразованиям Лоренца они оказываются неинвариантными. Из теории относительности следует, что уравнение динамики, инвариантное по отношению к преобразованиям Лоренца, имеет вид:
Мы приходим к выводу, что релятивистский импульс частицы равен Релятивистская масса. Определив массу частицы m как коэффициент пропорциональности между скоростью и импульсом, получим, что масса частицы зависит от ее скорости.
Вопрос 25. Вопрос 14. Особенности вращательного движения.
Рассмотрим движение твердого тела, имеющею ось вращения O1O2 под действием произвольно направленной силы F, приложенной к телу в некоторой точке А, которую можно разложить на две составляющие: вертикальную и горизонтальную (рис.5.1). Вертикальная составляющая может вызывать перемещение тела в направлении оси вращения поэтому при рассмотрении вращательного движения ее можно исключить, как.Горизонтальная составляющая Fr, если она не пересекается с осью O1O2 вызывает вращение тела. Действие этой силы зависит от ее числового значения и расстояния линии действия от оси вращения. Момент силы. Пусть на тело, в плоскости перпендикулярной оси вращения O1O2 действует сила F (рис.5.2). Разложим эту силу на две составляющие: Fn и Fe
Сила Fn пересекает ось вращения и, следовательно, не влияет на вращение тела. Под действием составляющей Fe тело будет совершать вращательное движение вокруг оси O1O2. Расстояние r от оси вращения до линии, вдоль которой действует сила Fe, называется плечом силы Fe. Моментом силы относительно точки О называется произведение модуля силы Fx на плечо r: M=Fer. С учетом, что Fx=Fsina, => момент силы M=rFsina. С точки зрения векторной алгебры это выражение представляет векторное произведение радиуса-вектора r, проведенного в точку приложения силы F на эту силу. Таким образом, момент силы относительно точки О является векторной величиной и равен M=[r,F]. Вектор момента силы направлен перпендикулярно к плоскости, проведенной через векторы r и F, и образует с ними правую тройку векторов (при наблюдении из вершины вектора М видно, что вращение по кратчайшему расстоянию от r к F происходит против часовой стрелки). Момент инерции. Согласно второму закону Ньютона, для тангенциальной составляющей силы Fix, действующей на материальную точку массой m, и ускорения aix можем записать: Fix=miaix. С учетом, что Fix=Fisina и aix=riƐ, Имеем Fisina=miriƐ. Домножим левую и правую части на ri и получим: riFisina= miri2Ɛ, Или Mi== miri2Ɛ. Произведение массы материальной точки m1 тела на квадрат ее расстояния ri2 до оси вращения называется моментом инерции материальной точки относительно оси вращения: Ji=miri2. Теорема Штейнера. Момент инерции тела J любой оси вращения равен моменту его инерции J0 относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы m тела на квадрат расстояния a между ними J=J0+ma2. Закон Ньютона. Вращающий момент тела: M=JƐ. Это выражение представляет собой аналог второго закона Ньютона для вращательного движения, из которого следует, что угловое ускорение Ɛ твердого тела при вращении вокруг неподвижной оси прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции Относительно этой оси. Из этого выражения следует, что момент инерции U является мерой его инертности во вращательном движении вокруг неподвижной оси. В случае поступательного движения мерой инертности, как известно, является масса тела.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 681; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |





 т.е.
т.е. 





 ;
; 

 ,
,  и
и 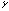 в преобразования координат (6.3) и (6.4) находим:
в преобразования координат (6.3) и (6.4) находим:






 .
.

 ;
; 
 где m0- инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы, F- сила действующая на частицу. Сопоставим с классическим уравнением
где m0- инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы, F- сила действующая на частицу. Сопоставим с классическим уравнением