Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Релятивистский закон сложения скоростей.Содержание книги Поиск на нашем сайте
Пусть в системе отсчета K’ материальная точка движется вдоль оси х’ спостоянной скоростью v’=x’/t’. Система K’ движется относительно системы K в том же направлении со скоростью v, Определим, чему равна скорость материальной точки vo, относительно системы K, т.е. чему равно v0=x/t. Пусть при t=t’=0 м.т. находится в начале координат, причем x=x’=0. Для системы K:
Подставляя x и t в формулу для vo:
Делим числитель и знаменатель на t:
Это равенство выражает собой релятивистский закон сложения скоростей. При малых значениях скоростей v’<<c и v<<c имеем v’v/c2<<1 и v0≈v’+v, т.е. релятивистский закон сложения скоростей переходит в классический
Вопрос 22. Следствия из преобразований Лоренца 1. Если в одной системе отсчета некоторые события происходят в точках x 1 и x 2 в один и тот же момент вр емени t, то в другой системе отсчета эти события происходят в точках x '1 и x '2 в разные моменты времени t '1 и t '2: t1’-t2’=u(x2’-x1’)/c2 Понятие одновременности оказывается зависящим от выбора системы отсчета. 2. Если в одной системе отсчета между двумя событиями, происходящими в одной и той же точке, проходит время t, то в другой системе отсче та между этими же событиями проходит время
Это соотношение выражает релятивистский эффект замедления времени в движущихся объектах. 3. Если в одной системе отсчета покоящаяся линейка имеет длину l, то в системе отсчета, в которой линейка движется со скоростью u вдоль своей оси, ее длина
Этот эффект называется релятивистским сокращением продольных размеров тела. Поперечные размеры тела не изменяются при переходе в другие инерциа льные системы отсчета. 4. Если в одной системе отсчета тело имеет скорость v = (vx, vy, vz), то его скорос ть v ' = (v'x, v'y, v'z) в другой системе отсчета равна
или в трехмерной векторной форме 5. Из соотношени (n4), (n5) следует постоянство скорости c в различных системах отсчета. Действительно, если вычислить сумму квадратов левых частей этих равенств при условии v 2=(vx)2+(vy) 2+(vz) 2= c 2, (n6) получим v' 2=(v'x)2+ (v'y)2+(v'z) 2= c 2. (n7) Т. е. скорость c одинакова по величине во всех инерциальных системах отсчета (независимо от направления). Заметим, что направления скоростей v и v ' в общем случае различны в разных системах отсчета. Лоренцево сокращение длины
Пусть l0 = x'2 – x'2 – собственная длина тела в системе, относительно которого тело неподвижно (например: в ракете, движущейся со скоростью мимо неподвижной системы отсчета k (Земля)). Измерение координат x1 и x2 производим одновременно в системе k, т.е. t1 = t2 = t. Используя преобразования Лоренца, для координат получим:
Тогда
Формулы (8.4.6) описывают лоренцево сокращение длин. Собственная длина тела есть максимальная длина. Длина движущегося тела короче, чем покоящегося. Причем сокращается только проекция на ось x, т.е. размер тела вдоль направления движения. Вопрос 23. Следствия из преобразований Лоренца 1. Если в одной системе отсчета некоторые события происходят в точках x 1 и x 2 в один и тот же момент вр емени t, то в другой системе отсчета эти события происходят в точках x '1 и x '2 в разные моменты времени t '1 и t '2: t1’-t2’=u(x2’-x1’)/c2 (n1) Понятие одновременности оказывается зависящим от выбора системы отсчета. 2. Если в одной системе отсчета между двумя событиями, происходящими в одной и той же точке, проходит время t, то в другой системе отсче та между этими же событиями проходит время
Это соотношение выражает релятивистский эффект замедления времени в движущихся объектах. 3. Если в одной системе отсчета покоящаяся линейка имеет длину l, то в системе отсчета, в которой линейка движется со скоростью u вдоль своей оси, ее длина
Этот эффект называется релятивистским сокращением продольных размеров тела. Поперечные размеры тела не изменяются при переходе в другие инерциа льные системы отсчета. 4. Если в одной системе отсчета тело имеет скорость v = (vx, vy, vz), то его скорос ть v ' = (v'x, v'y, v'z) в другой системе отсчета равна
или в трехмерной векторной форме 5. Из соотношени (n4), (n5) следует постоянство скорости c в различных системах отсчета. Действительно, если вычислить сумму квадратов левых частей этих равенств при условии v 2=(vx)2+(vy) 2+(vz) 2= c 2, (n6) получим v' 2=(v'x)2+ (v'y)2+(v'z) 2= c 2. (n7) Т. е. скорость c одинакова по величине во всех инерциальных системах отсчета (независимо от направления). Заметим, что направления скоростей v и v ' в общем случае различны в разных системах отсчета. Замедление времени Пусть вспышка лампы на ракете длится τ = t'2 – t'1, где τ – собственное время, измеренное наблюдателем, движущимся вместе с часами. Чему равна длительность вспышки (t2 – t1) с точки зрения человека, находящегося на Земле, мимо которого пролетает ракета?
Так как x'1 = x'2 то из преобразований Лоренца
Из этого уравнения следует, что собственное время – минимально (движущиеся часы идут медленнее покоящихся). Таким образом, вспышка на Земле будет казаться длиннее. Этот вывод имеет множество экспериментальных подтверждений. Так, нестабильные элементарные частицы – пионы, рождающиеся в верхних слоях атмосферы, на высоте 20–30 км, при воздействии на нее космических лучей имеют собственное время жизни τ ~ 2·10-6 с. За это время они могут пройти короткий путь S = c·τ = 600 м. Но в результате того, что они двигаются с очень большими скоростями, сравнимыми со скоростью света, их время жизни увеличивается и они до своего распада способны достигать поверхности Земли. Отсюда следует вывод, что у движущихся пионов секунды «длиннее» земных секунд. В 70-е г. замедление времени наблюдалось не только с помощью нестабильных микрочастиц, но и проводились прямые измерения с использованием высокоточных часов, основанных на эффекте Мессбауэра. Двое таких часов показывают одно и то же время с точностью до 10-16 с. В 1971 г. Хафель и Китинг осуществили прямое измерение замедления времени, отправив два экземпляра атомных часов в кругосветное путешествие на реактивном самолете. Потом их показания сравнили с показаниями таких же часов, оставленных на Земле, в лаборатории ВМС США. Время запаздывания составило 273·10-9 с, что в пределах ошибок согласуется с теорией. Это следствие из преобразований Лоренца объясняет известный всем «парадокс близнецов».
Вопрос 24. Релятивистский импульс. Уравнения классической механики инвариантны по отношению к преобразованиям Галилея, по отношению же к преобразованиям Лоренца они оказываются неинвариантными. Из теории относительности следует, что уравнение динамики, инвариантное по отношению к преобразованиям Лоренца, имеет вид:
Мы приходим к выводу, что релятивистский импульс частицы равен Релятивистская масса. Определив массу частицы m как коэффициент пропорциональности между скоростью и импульсом, получим, что масса частицы зависит от ее скорости.
|
||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.69.162 (0.012 с.) |


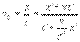
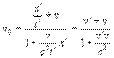





 .
.

 ;
; 
 где m0- инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы, F- сила действующая на частицу. Сопоставим с классическим уравнением
где m0- инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы, F- сила действующая на частицу. Сопоставим с классическим уравнением