
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства линейных операций с векторамиСодержание книги
Поиск на нашем сайте
Для любых векторов
Условие коллинеарности векторов: два ненулевых вектора Нулевой вектор считается коллинеарным любому вектору.
Скалярное произведение векторов
Скалярным произведением векторов Свойства скалярного произведения векторов Для любых векторов
Из определения скалярного произведения следует, что угол между ненулевыми векторами
Если хотя бы один из векторов нулевой, то угол Из формулы (1) следует условие ортогональности векторов: два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю, т.е.
(нулевой вектор считается ортогональным любому вектору). Механический смысл скалярного произведения: работа
4.Векторное произведение векторов
Векторным произведением векторов
образуют правую тройку, т.е. из конца вектора Замечание. Это определение однозначно определяет векторное произведение ненулевых векторов. Если хотя бы один из сомножителей — нулевой вектор, то векторное произведение считается равным нулевому вектору. Из определения векторного произведения следует, что Геометрический смысл векторного произведения: модуль векторного произведения векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах. Свойства векторного произведения векторов Для любых векторов
1. 2.
Условие коллинеарности векторов: два вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т.е.
(нулевой вектор можно считать коллинеарным любому вектору). Смешаное произведение векторов
Смешанным произведением векторов
т.е. векторное произведение двух векторов По определению скалярного и векторного произведений имеем ( причем знак (+) берется в том случае, когда угол θ острый, т.е. тройка векторов Геометрический смысл смешанного произведения: смешанное произведение векторов Свойства смешанного умножения векторов 1. Условие компланарности векторов: три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю. 2. ( 3. 4.
(Из примерного содержания практического пособия для учащихся) Вопросы к повторению темы «Прямая на плоскости»: 1. При каком условии прямая 2. При каком условии прямая 3. При каком условии прямая 4. При каком условии уравнение прямой 5. При каком условии прямые 6. При каком условии прямые 7. При каком условии прямые
Контрольная работа
|
||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 559; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.005 с.) |

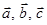 и любых чисел α, β:
и любых чисел α, β:
 и
и  коллинеарны тогда и только тогда, когда они пропорциональны, т.е. существует число (
коллинеарны тогда и только тогда, когда они пропорциональны, т.е. существует число (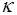 ) такое, что
) такое, что  .
. и равное произведению их модулей и косинуса угла
и равное произведению их модулей и косинуса угла  между ними, т.е.
между ними, т.е. 

 определяется формулой
определяется формулой

 постоянной силы
постоянной силы  , действующей на материальную точку, при ее перемещении из точки
, действующей на материальную точку, при ее перемещении из точки  определяется формулой
определяется формулой 
 , который обозначается
, который обозначается  и удовлетворяет следующим трем условиям:
и удовлетворяет следующим трем условиям: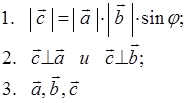
 виден против часовой стрелки.
виден против часовой стрелки. для любого вектора
для любого вектора  и любых чисел α, β:
и любых чисел α, β: , т.е. векторное произведение антикоммутативно;
, т.е. векторное произведение антикоммутативно; , т.е. векторное произведение дистрибутивно относительно сложения;
, т.е. векторное произведение дистрибутивно относительно сложения; , т.е. векторное произведение ассоциативно относительно вещественного множителя.
, т.е. векторное произведение ассоциативно относительно вещественного множителя.
 ) и определяемое равенством
) и определяемое равенством ,
,
 умножается скалярно на третий вектор
умножается скалярно на третий вектор  .
. ) = (
) = ( = =
= =  ,
, — угол между векторами
— угол между векторами  , а
, а  — угол между векторами (
— угол между векторами ( ) и
) и  операции векторного и скалярного умножения в смешанном произведении можно менять местами;
операции векторного и скалярного умножения в смешанном произведении можно менять местами; в смешанном произведении можно осуществлять круговую перестановку множителей местами;
в смешанном произведении можно осуществлять круговую перестановку множителей местами; в смешанном произведении при перестановки двух множителей местами меняется знак произведения на противоположный;
в смешанном произведении при перестановки двух множителей местами меняется знак произведения на противоположный;
 проходит через начало координат?
проходит через начало координат? и
и 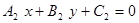 пересекаются?
пересекаются?


