
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
до базиса векторного пространства.Содержание книги
Поиск на нашем сайте
Теорема 1. Пусть V – n-мерное векторное пространство над полем Р, (1) ā1,…,āk – линейно независимая система векторов из V. Тогда система (1) может быть дополнена до базиса векторного пространства V. Доказательство. Если k=n, то (1) – базис векторного пространства V. Пусть k < n. Рассмотрим линейную оболочку, натянутую на векторы системы (1): V1=L(ā1,…,āk)={ Пространство всех решений однородной системы уравнений. Фундаментальный набор решений однородной системы Линейных уравнений. Теорема 1. Пусть (1) Доказательство проводится непосредственной проверкой с помощью критерия подпространства. Определение 1. Пусть (1) Найдём фундаментальный набор решений системы (1). Пусть x1,…,xk – главные неизвестные, остальные – свободные неизвестные. Составим систему векторов из U по следующему правилу (*): придадим первой свободной неизвестной значение 1, остальным свободным неизвестным – значение 0, получим вектор (2) Покажем, что (2) – базис векторного пространства U. 1) Покажем, что система (2) линейно независима. Пусть (3)
2) Покажем, что через векторы системы (2) линейно выражается каждый вектор из U. Пусть
Так как (2) Из 1) и 2) => система (2) - базис U => система (2) – фундаментальный набор решений системы (1). Вывод: Для того, чтобы найти фундаментальный набор решений однородной системы линейных уравнений, необходимо решить систему методом Гаусса и записать систему Связь между решениями неоднородной системы линейных уравнений с решениями ассоциированной с ней однородной системы линейных уравнений. Лемма 1. Пусть (1) 1) Если 2) Если Доказательство. 1) Так как
2) Так как
Теорема 1. Пусть (1) - неоднородная система линейных уравнений над полем P, (2) - однородная система линейных уравнений, ассоциированная с (1), Н – множество всех решений системы (1), U - множество всех решений системы (2), Доказательство. Докажем, что Н = а) Покажем, что б) Покажем, что Из а) и б) следует, что Н = Замечание. Из теоремы 12 следует, что для того, чтобы найти множество всех решений системы (1), достаточно найти множество всех решений системы (2) и хотя бы одно решение системы (1).
Строчечный и столбцовый ранги матрицы. Теорема Кронекера-Капелли. Рассмотрим матрицу A над полем P размера m×n следующего вида:
Определение 1. Вектор Таким образом, (1) - система векторов-строк матрицы А, (2) - система векторов-столбцов матрицы А. Определение 2. Строчным (горизонтальным) рангом матрицы называется ранг её системы векторов-строк, и обозначается rг(A). Столбцовым (вертикальным) рангом матрицы называется ранг её системы векторов-столбцов и обозначается rв(A). Лемма 1. При элементарных преобразовании матрицы строчный и столбцовый ранги матрицы не изменяются. Теорема 1. Строчечный и столбцовый ранги матрицы А совпадают, т.е. rг(A)=rв(A); и обозначается r(A); число r(A) называется рангом матрицы А. Доказательство. Пусть А - матрица размера m×n над полем Р. Покажем что rг(A)=rв(A). Для этого приведём матрицу А с помощью элементарных преобразований к ступенчатому виду А' размера r×n: Покажем что rг(A')=r. Рассмотрим систему векторов-строк матрицы А': Пусть
Умножая и складывая векторы покоординатно, получим систему уравнений
И, поскольку Значит, (1') - линейно независимая система векторов. Тогда (1') - базис системы (1'), и значит, ранг системы (1') равен r, т.е. rг(A')=r. 2) Покажем, что rв(А')=r. Рассмотрим систему а) Покажем, что (3) - линейно независимая система векторов. Пусть
Так как ars б) Так как (3) - линейно независимая система векторов, состоящая из r векторов, и dimpPr=r, то (3) - базис Pr. В силу (2') – система векторов из Pr, получаем, что (3) - базис системы (2'). Таким образом, rв(A')=r Исходя из доказанной теоремы, определение ранга матрицы часто формулируют следующим образом: Определение 3. Рангом матрицы A называется ранг её системы векторов-строк, и обозначается r(A). Теорема 1 (теорема Кронекера-Капелли). Пусть (4) Доказательство. Пусть система (4) совместна
В случае, когда r(A)=r( Замечание. Однородная система линейных уравнений имеет единственное решение тогда и только тогда, когда ранг её матрицы равен числу неизвестных. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ранг её матрицы меньше числа неизвестных.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.219.221 (0.007 с.) |

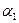 ā1+…+
ā1+…+  āk|
āk| 
 P, i=
P, i=  }. Отметим, что V1
}. Отметим, что V1  V. Так как k<n, то V1
V. Так как k<n, то V1 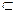 V. Пусть āk+1
V. Пусть āk+1 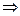 вектор āk+1 является линейной комбинацией векторов ā1,…,āk
вектор āk+1 является линейной комбинацией векторов ā1,…,āk  - однородная система линейных уравнений над полем P, U – множество всех решений системы (1), т.е. U =
- однородная система линейных уравнений над полем P, U – множество всех решений системы (1), т.е. U = 
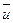 - решение системы (1)
- решение системы (1) 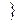 . Тогда множество U является подпространством векторного пространства V=Pn.
. Тогда множество U является подпространством векторного пространства V=Pn. - однородная (неопределенная) система линейных уравнений над полем P, U – векторное пространство всех решений системы (1). Базис векторного пространства U называется фундаментальным набором решений однородной системы линейных уравнений (1).
- однородная (неопределенная) система линейных уравнений над полем P, U – векторное пространство всех решений системы (1). Базис векторного пространства U называется фундаментальным набором решений однородной системы линейных уравнений (1). ; придадим второй свободной неизвестной значение 1, остальным свободным неизвестным – значение 0, получим вектор
; придадим второй свободной неизвестной значение 1, остальным свободным неизвестным – значение 0, получим вектор  , и т.д. Получим систему вида:
, и т.д. Получим систему вида: .
.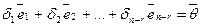 . Покажем, что
. Покажем, что  i =0, i =1,
i =0, i =1,  . Из (3) =>
. Из (3) =>
 . Это означает, что система (2) линейно независима.
. Это означает, что система (2) линейно независима.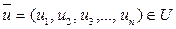 . Покажем, что вектор
. Покажем, что вектор  линейно выражается через (2). Рассмотрим вектор
линейно выражается через (2). Рассмотрим вектор  следующего вида:
следующего вида:
 . Поскольку
. Поскольку 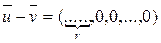 и (1) -однородная система линейных уравнений, то
и (1) -однородная система линейных уравнений, то  =>
=>  =>
=>  по правилу (*).
по правилу (*).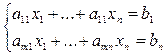 - неоднородная система линейных уравнений над полем P, (2)
- неоднородная система линейных уравнений над полем P, (2)  - однородная система линейных уравнений, ассоциированная с (1). Тогда выполняются следующие условия:
- однородная система линейных уравнений, ассоциированная с (1). Тогда выполняются следующие условия: и
и  - решения системы (1), то
- решения системы (1), то  - решение системы (2).
- решение системы (2).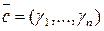 - решение системы (1) и
- решение системы (1) и  - решение (2), то
- решение (2), то  - решение системы (1).
- решение системы (1). - решение (1), то
- решение (1), то  . Так как
. Так как  - решение (1), то
- решение (1), то  . Тогда
. Тогда ,
,  =>
=>  . Так как
. Так как  . Тогда
. Тогда ,
,  =>
=> 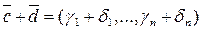 - решение системы (1). Лемма доказана.
- решение системы (1). Лемма доказана.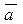 - некоторое решение системы (1). Тогда Н =
- некоторое решение системы (1). Тогда Н =  .
. . Пусть
. Пусть 
 =
=  =>
=>  . Пусть
. Пусть 

 и
и  - решение системы (1)
- решение системы (1)  =>
=>  =>
=>  . Пусть
. Пусть
 называется i-й вектор-строкой матрицы А,
называется i-й вектор-строкой матрицы А,  ; вектор
; вектор  называется j-м вектор-столбцом матрицы А,
называется j-м вектор-столбцом матрицы А,  .
. , где a'11
, где a'11  0, a'2k
0, a'2k  (1'). Покажем, что ранг системы (1') равен r. Для этого достаточно показать, что (1') - линейно независимая система векторов.
(1'). Покажем, что ранг системы (1') равен r. Для этого достаточно показать, что (1') - линейно независимая система векторов. - нулевая линейная комбинация системы (1'). Покажем, что все коэффициенты
- нулевая линейная комбинация системы (1'). Покажем, что все коэффициенты 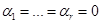 . В координатной форме нулевая линейная комбинация имеет вид
. В координатной форме нулевая линейная комбинация имеет вид

 выражая коэффициенты ai поочередно из всех уравнений, начиная с первого, получим
выражая коэффициенты ai поочередно из всех уравнений, начиная с первого, получим 
 (2’) векторов-столбцов матрицы А'. Так как вектор
(2’) векторов-столбцов матрицы А'. Так как вектор  имеет r координат, то
имеет r координат, то  Поскольку Pr - это r- мерное векторное пространство, т.е. dimpPr=r, то ранг системы (2) меньше либо равен r, т.е. rв(A')≤r. Рассмотрим систему векторов
Поскольку Pr - это r- мерное векторное пространство, т.е. dimpPr=r, то ранг системы (2) меньше либо равен r, т.е. rв(A')≤r. Рассмотрим систему векторов  (3) (всего r векторов; эти векторы соответствуют элементам a'11
(3) (всего r векторов; эти векторы соответствуют элементам a'11 
 s =0; …; так как a2k
s =0; …; так как a2k 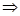 rг(A')= rв(A')
rг(A')= rв(A')  - соответственно основная и расширенная матрицы системы (4). Система (4) совместна
- соответственно основная и расширенная матрицы системы (4). Система (4) совместна  r(A)=r(
r(A)=r( (*), где
(*), где (5) - система векторов-столбцов матрицы А,
(5) - система векторов-столбцов матрицы А, (6) - система векторов-столбцов матрицы
(6) - система векторов-столбцов матрицы  является линейной комбинацией векторов системы (5)
является линейной комбинацией векторов системы (5) 


