
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подпространство. Критерий подпространства.Содержание книги
Поиск на нашем сайте
Определение 1. Подмножество H векторного пространства V над полем Р называется подпространством векторного пространства V, если H является векторным пространством над полем Р относительно тех же операций, что и векторное пространство V. Теорема 1 (Критерий подпространства). Пусть H - непустое подмножество векторного пространства V над полем Р. Н является подпространством векторного пространства V тогда и только тогда, когда выполняются два условия: 1) 2) Доказательство. 1. Необходимость ( ⇒ ). Пусть Н – подпространство векторного пространства V над полем Р. Тогда по определению 1 Н – векторное пространство над полем Р. По определению векторного пространства множество Н является замкнутым относительно сложения и относительно умножения векторов из Н на элементы из поля Р, т.е. выполняются условия 1) и 2). 2. Достаточность(⇐). Пусть выполняются условия 1) и 2). Покажем, что Н – подпространство векторного пространства V. В силу определения подпространства, достаточно показать, что Н – векторное пространство над полем Р. Из условий 1) и 2) следует, что множество Н замкнуто относительно сложения и относительно умножения элементов из Н на элементы из поля Р. Проверим для Н выполнимость аксиом векторного пространства. Предварительно отметим что, так как Покажем, что для Н выполняется аксиома I 2). Так как Покажем, что для Н выполняется аксиома I 3). Пусть Таким образом, Н – векторное пространство над полем Р. По определению подпространства получаем, что Н – подпространство векторного пространства V. Теорема доказана.
Линейно зависимые и линейно независимые системы векторов. Определение 1. Пусть V – векторное пространство над полем P, Определение 2. Пусть V – векторное пространство над полем P,
Простейшие свойства линейно зависимой системы векторов. Свойство 1. Система векторов является линейно зависимой Свойство 2. Пусть V – векторное пространство над полем P. Если система векторов Доказательство. Пусть, например, Свойство 3. Если система векторов содержит линейно зависимую подсистему, то она линейно зависима, т.е. если Доказательство. Так как система (2) линейно зависима, то по определение 1 Свойство 4. Если система векторов (1) Доказательство. Так как система (4) линейно зависима, то по определению 1
Покажем, что
Свойство 5. Если большая система линейно выражается через меньшую, то большая система линейно зависима. Другими словами, пусть Следствие 5.1. Пусть каждый вектор системы (1)
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2989; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.82.60 (0.005 с.) |

 ;
;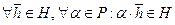 .
.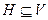 и V – векторное пространство над полем Р, то в Н выполняются обобщенные дистрибутивные законы; обобщенный ассоциативный закон; унитарный закон; ассоциативность и коммутативность сложения.
и V – векторное пространство над полем Р, то в Н выполняются обобщенные дистрибутивные законы; обобщенный ассоциативный закон; унитарный закон; ассоциативность и коммутативность сложения. ∅, то существует
∅, то существует 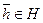 . Тогда
. Тогда  , т.е.
, т.е. 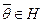 . Это означает, что выполняется аксиома I 2).
. Это означает, что выполняется аксиома I 2). . Тогда по условию 2)
. Тогда по условию 2) 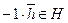 . Отсюда, по унитарному закону, следует, что
. Отсюда, по унитарному закону, следует, что 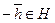 . Следовательно, выполняется аксиома I 3).
. Следовательно, выполняется аксиома I 3).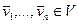 . Система векторов
. Система векторов 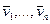 называется линейно зависимой, если
называется линейно зависимой, если  Р, не равные 0 одновременно, такие что
Р, не равные 0 одновременно, такие что  .
.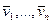 называется линейно независимой, если
называется линейно независимой, если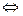
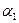 = 0,
= 0, 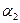 = 0,...,
= 0,..., 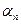 = 0.
= 0.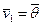 . Тогда
. Тогда 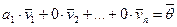 , где
, где 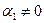 . Это означает, что система (1) линейно зависима. Свойство доказано.
. Это означает, что система (1) линейно зависима. Свойство доказано.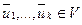 (2),
(2), 

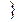
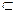
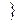 , (2) – линейно зависима, то система (1) линейно зависима.
, (2) – линейно зависима, то система (1) линейно зависима.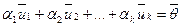 (3). Пусть, например,
(3). Пусть, например, 
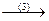
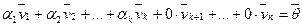
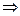 по определению 1 система (1) линейно зависима. Свойство доказано.
по определению 1 система (1) линейно зависима. Свойство доказано.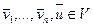 линейно зависима, то вектор
линейно зависима, то вектор 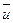 является линейной комбинацией векторов системы (1), т.е. говорят, что вектор
является линейной комбинацией векторов системы (1), т.е. говорят, что вектор 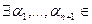 Р, не равные нулю одновременно, такие что
Р, не равные нулю одновременно, такие что (5).
(5).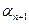
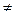 0. Допустим, что
0. Допустим, что  не равны 0 одновременно
не равны 0 одновременно 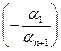
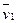 +
+ 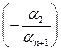
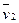 +... +
+... + 
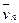 . Таким образом, вектор
. Таким образом, вектор  (6), и каждый вектор системы (1) линейно выражается через векторы системы (6). Если n > r, то система (1) линейно зависима.
(6), и каждый вектор системы (1) линейно выражается через векторы системы (6). Если n > r, то система (1) линейно зависима. r.
r.


