Энергетическая диаграмма для атома водорода.

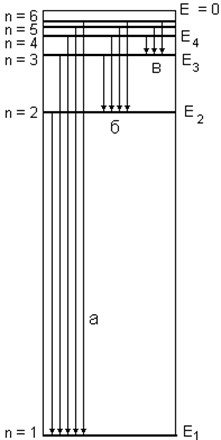
Поскольку излучение света на той или иной длине волны связано с испусканием энергии атомом, то была предложена нижеследующая схема его энергетических состояний (см. рис.3).

Излучаемая водородным атомом в виде света энергия представляется на энергетической диаграмме как переход электрона с более высоких уровней на второй. Именно переходы на второй уровень описывались эмпирической формулой Бальмера, поэтому и серия переходов и, соответственно, спектральных линий в видимой области получила название серии Бальмера (рис.3б). В принципе, возможны и осуществляются переходы и на первый уровень, однако они приходятся уже на ультрафиолетовую область – это так называемая серия Лаймана (рис.3а). Переходы на третий уровень со всех расположенных выше описываются как серия Пашена, они попадают уже в инфракрасную область (рис. 3в).

Эмиссионные спектры (спектры излучения) возникают при тер­мическом возбуждении атомов в вольтовой дуге или в разряде.

Наиболее характерной чертой спектров, излучения атомов яв­ляется их дискретность. Спектры состоят из набора линий, каждая из которых соответствует определенной длине волны (рис.2).

 

 

 

 

Рис.2. Спектр атома водорода.

 

 

Рис.3. Схема энергетических

уровней атома водорода.

 

Шведским ученым Ридбергом предложена следующая формула, описывающая энергетические переходы в одноэлектронном атоме (ионе):

 

Δ E = R · Z² (1/n_i² - 1/ n_j² ). (10)

 

Здесь главные квантовые числа для различных уровней обозначены как n_i = 1, 2, 3, 4, 5..., n_j = 2, 3, 4, соответственно. Это выражение получается из термов электрона на различных энергетических уровнях, см. формулу (1).

Пользуясь уравнением Ридберга (10) и приведенной выше формулой Планка (2), можно рассчитать длины волн испускаемого излучения l_ji при переходах электрона в атоме с энергетических уровней n_j на энергетический уровень n_i, соответствующих спектральных серий, в частности длины волн серии Бальмера:

 

h × c

l_j2 = ¾¾¾¾¾¾. (11)

R×(1/n₂² – 1/n_j²)

Экспериментальная часть.

Цель работы - изучение эмиссионных спектров атомарного во­дорода и ртути и неизвестного элемента; идентификация неизвестного элемента с использованием табличных данных.

 

Характеристичность спектров атомов позволяет использовать их для идентификации элементов. Каждому химическому элементу соответствует свой характеристический набор линий в спектре. Идентификация химического элемента может осуществляться, как минимум, по трем линиям его эмиссионного спектра.

Для изучения эмиссион­ных спектров, используются спектральные приборы, которые обеспечивают разложение све­та, идущего от источника излу­чения, в спектр по длинам волн. Спектральный прибор имеет три основные части (рис.4):

а) коллиматор часть с узкой щелью (входная щель прибора), ус­тановленной в фокусе объек­тива коллиматора;

б) диспергирующий элемент (спектральная призма или дифракционная решетка);

в) камерный объектив, который собирает на своей фокальной поверхности параллельные пучки и дает монохроматическое изоб­ражение входной щели, соответствующее различным длинам волн.

 

 

 

Рис.4. Схема спектрального прибора.

Приборы и источники излучения:

1. Спектральный прибор - монохроматор УМ-2.

2. Ртутная лампа, водородная лампа и лампа с неизвестным элемен­том.

3. Источники питания ламп.

Порядок выполнения работы.

1. Ознакомиться с инструкцией по работе на спектральном приборе. Под руководством лаборанта подготовить УМ-2 к работе.

2. Провести градуировку прибора по линиям спектра ртути. Для этого подключить ртутную лампу к источнику питания и поместить ее перед входной щелью прибора. Вращая бараба­н, вывести указатель на середину желтой линии в спектре излучения ртути. Наблюдение вести через окуляр прибора.

Необходимо устанавливать указатель в окуляре на середину линии, после чего снимать отсчет по шкале барабанчика. Затем перейти к следую­щей линии и т.д. Резуль­таты представить по прилагаемой форме (Табл.2.).

3. Подключить водородную лампу к источнику питания. Медлен­но вращая рукоятку барабанчика, вывести указатель последовательно на четыре линии, снимая отсчет по шкале барабанчика.

4. Подключить лампу с неизвестным элементом к источнику пи­тания, произвести отсчет делений барабанчика для каждой линии.

 

Таблица 2.

Градуировка монохроматора

 

Элемент	Цвет линий	Длина волны, нм	Деление барабана
Ртуть	Фиолетовая	404,6
Синяя	435,8
Голубая	491,6
Зеленая	546,1
Желтая	577,0

 

Обработка результатов.

1. Используя данные, полученные для ртутной лампы (табл.2.), построить на миллиметровке градуировочный график зависимости длины волн от числа делений шкалы барабана монохроматора l = f (дел.). Примерный вид графика представлен на рис. 5.

2. Ис­пользуя построенный по результатам измерений градуировочный график, определить по делениям барабана длины волн обнаруженных спектральных линий атомарного водорода.

3. Используя градуировочный график, определить длины волн излучения лампы, содер­жащей неизвестный элемент, и, сопоставив с длинами волн, приве­денными в таблице 3, определить этот элемент.

 

l,нм

Рис. 5. Калибровочный график монохроматора.

 

Таблица 3.

Характеристические линии в спектрах испускания

атомов некоторых химических элементов

Элемент	Длины волн наиболее интенсивных линий, нм
Нg	546,1	435,8	404,7	577,0 / 579,0
Na	589,5	588,8	568,8
Ca	445,4	443,5	422,7
Cs	852,1	459,3	455,5
Cd	508,6	482,0	480,8	468,0	467,8	472,2

 

4. Используя формулы (10) и (11), приведенные в теоретической части работы, вычислить теоре­тические значения длин волн линий серии Бальмера атомов водо­рода, сопоставить их с экспериментально измеренными и заполнить представленные ниже таблицы 4 и 5.

5. Полученную экспериментально длину волны для водородной лампы сравнить с теоретическим значением, вычислить погрешность измерений.

 

Таблица 4.

Спектральные данные для атомарного водорода

Эле-мент	Цвет линии	Деления бараба-на	Длина вол-ны экспе-рименталь-ная lэ, нм	Длина волны расчетная lj2, нм	Энерге-тический переход n j → n2	Энергия перехода ΔЕ, Дж
Водо-род	Фиолет.
Синяя
Голубая
Красная

 

 

Таблица 5.

Спектральные данные для атомов неизвестного элемента

Элемент	Номер линии	Деления барабана	Длина волны эксперименталь- ная lэ, нм	Длина волны табличная lэ, нм	Элемент
Неизвестный элемент

 

Литература.

1. Угай Я.А. Общая химия. - М, Высшая школа. 1984.

2. Карапетьянц М.Х., Дракин А.П., Строение вещества. - М.: Высшая школа, 1989.

3. Мешковский И.K., Попков O.С. Строение вещества и химическая связь. Учебное пособие. СПбГИТМО(ТУ), 1999.

4. Новиков А.Ф., Успенская М.В. Электронный учебник по курсу химии, глава 2 "Современные представления о строении и свойствах атомов, Пeриoдичeский зaкoн Д.И.Мeндeлeeвa", раздел 2.2. Центр дистанционного обучения СПбГУИТМО, 2004.

 

 

Лабораторная работа № 3

 

ОПРЕДЕЛЕНИЕ ДИПОЛЬНОГО МОМЕНТА МОЛЕКУЛЫ.

 

Теоретическая часть.

 

Дипольные моменты позволяют получить информацию о структуре молекул. С практической точки зрения они важны для нахожде­ния подходящего растворителя для данного твердого вещества, так как способность растворителя разрушать связь в ионном кристалле связа­на с его способностью полярной молекулы уменьшать электро­статическое взаимодействие между ионами в кристалле и сольватировать ионы.

Дипольный момент является векторной количественной харак­теристикой полярности молекулы. Существование или отсутствие электрического дипольного момента у молекулы связано с ее сим­метрией. Если электрические центры тяжести положительных и от­рицательных зарядов совпадают, то такие молекулы неполярны (О₂, N₂, ССl₄ и др.). Если электрические цент­ры тяжести не совпадают (например, гетероядерные двухатомные молекулы, такие как HCl, NaF, или многоатомные молекулы Н₂О, CH₃Cl), то в молекуле образуется пос­тоянный электрический диполь - система двух равных по величине и противоположных по знаку зарядов, разделенных некоторым расстоя­нием. Такие молекулы полярны и характеризуются постоянным дипольным моментом.

С точки зрения электростатики, полярная молекула представляет собой диполь, характеризуемый собственным дипольным моментом величиной

μ_с = q · l. Здесь l - длина диполя, а q - его электростатический заряд, который может быть представлен как q = δ · e (δ - эффективный заряд диполя, e - заряд электрона). Тогда собственный дипольный момент будет равен:

 

μ_с = δ · e · l. (1)

 

Эффективный заряд δ возникает в результате перераспределения электронной плотности при образовании молекулы, он соответствует степени ионности химической связи. Зная экспериментальное значение дипольного момента, можно рассчитать эффективный заряд:

 

d= m / e × l. (2)

 

Дипольный момент измеряется в Кл·м, однако практически более удобной оказалась внесистемная единица измерения – Дебай (Д): 1Д = 3,336·10^-30 Кл·м.

Дипольный момент – величина векторная, поэтому результирующий дипольный момент молекулы есть векторная сумма дипольных моментов связей внутри молекулы, что определяется ее стрoeниeм.

При помещении в статическое электрическое поле полярная молекула, естественно, ориентируется по силовым линиям поля, однако, помимо этого, она испытывает еще и дополнительную деформацию, связанную со смещением общего электронного облака молекулы в сторону положительного электрода и со смещением положительных ядер – в сторону отрицательного. Таким образом, к собственному дипольному моменту молекулы в электрическом поле добавляется момент, индуцированный внешним полем:

 

μ = μ_с + μ_инд. (3)

 

Неполярная молекула, естественно, имеет только индуцированный дипольный момент. Этот индуцированный дипольный момент молекулы μ_инд линейно зависит от напряженности локального электрического поля Е_лок , действующего на молекулу:

 

μ_инд = α_инд · Е_лок. (4)

 

Коэффициент пропорциональности имеет определенный физический смысл и называется индукционной (α_инд), или деформационной поляризуемостью (α_деф). Размерность поляризуемости оказывается соответствующей м³ или см³. Дальнейший анализ позволил установить, что значение поляризуемости примерно равно кубу радиуса молекулы, представляемой в виде сферы. Следовательно, объем молекулы может быть найден как (4π / 3) · α_деф. Тогда общий объем одного моля молекул будет равен:

 

ΣV_м = (4π / 3) · N_А· α_деф, (5)

 

где N_А – число Авогадро.

Деформационная поляризуемость, таким образом, включает в себя электронную и атомную составляющие:

 

α_деф = α_эл + α_ат . (6)

 

В случае полярной молекулы поляризуемость включает в себя еще и ориентационную составляющую α_ор:

 

α = α_деф + α_ор = α_эл + α_ат + α_ор . (7)

 

Установлено, что ориентационная составляющая поляризуемости α_ор связана с собственным дипольным моментом молекулы μ_с следующим образом:

 

α_ор = μ_с² / 3kT, (8)

 

здесь k - постоянная Больцмана, Т - температура.

Если мы имеем дело не с одной молекулой, а с веществом, содержащим моль (число Авогадро N_А) молекул, удобнее оперировать не поляризуемостью, а так называемой поляризацией вещества в электрическом поле:

 

P_М = μ · N_А / V_М , (9)

 

где V_М = М / ρ – это мольный объем вещества.

Обнаружилось, что поляризация тоже зависит от напряженности внешнего электрического поля Е:

 

P_М = [(ε – 1) / 4π] · E. (10)

 

Здесь ε – диэлектрическая проницаемость вещества. Связь между напряженностями внешнего Е и локального Е_лок электрических полей дается соотношением:

 

Е_лок = [(ε + 2) / 3] · E. (11)

 

Комбинируя эти выражения, получаем формулу Клаузиуса-Моссотти для мольной поляризации вещества:

 

P_М = [(ε – 1) / (ε + 2)] · V_М = (4π / 3) · N_А· α, (12)

или: P_М = [(ε – 1) / (ε + 2)] · (M / ρ) = (4π / 3) · N_А· α. (13)

 

Объединяя эти формулы, получаем уравнение, впервые выведенное П. Дебаем:

 

P_М = [(ε – 1) / (ε + 2)] · V_М = (4π / 3) · N_А · (α_эл + α_ат + μ_с² / 3kT). (14)

 

Уравнение Дебая является точным для разреженных газов и лишь приближенно выполняется для слабо полярных жидкостей, но практически не применимо к жидкостям с высокой диэлектрической проницаемостью.

Уравнение Дебая не учитывает взаимодействия между полярными молеку­лами, поэтому для экспериментального определения дипольного мо­мента молекул используют метод разбавленных растворов. При раз­бавлении раствора, содержащего полярное вещество, например, ацетон (СН₃)₂СО в неполярном растворителе (четыреххлористый углерод ССl₄), взаимодействие между молекулами ацетона уменьшается по мере того, как увеличивается расстояние между ними. Диэлектрические свойства раствора определяют при использовании этого метода по изменению электрической емкости конденсаторов, заполненных растворами по­лярного вещества различной концентрации. При этом емкость кон­денсаторов возрастает с увеличением содержания полярного ве­щества.

Как и поляризуемость, поляризация может быть представлена в виде суммы трех составляющих:

 

P_М = P_эл + P_ат + P_ор = Р_деф + P_ор , (15)

 

где Р_эл = (4/3)pN_Aa_эл – поляризация электронного типа;

Р_ат = (4/3)pN_Aa_ат – атомная поляризация;

Р_ор = (4/3)pN_Aa_ор = μ_с² / 3kT – ориентационная поляризация;

Р_деф = (4/3)pN_Aa_деф – деформационная поляризация.

 

Дипольный момент молекулы μ может быть найден, в частности, с использованием метода разделения составляющих поляризации по частоте. Дело в том, что при низких частотах осцилляции внешнего электрического поля осуществляются все три вида поляризации (атомная, электронная и ориентационная). При высоких же частотах, соответствующих частотам колебаний электромагнитного поля видимого света, проявляется, в основном, только электронная составляющая поляризации, которая может быть найдена через показатель преломления молекулярного вещества n по уравнению Лоренца-Лорентца. Это уравнение выведено для поведения молекул в высокочастотном поле, приближающемся к частотам колебаний видимого света. В этих условиях говорят уже не о диэлектрической проницаемости вещества ε, а о его показателе преломления n, связь между ними дается соотношением Максвелла ε ≈ n²:

 

P_эл = R_М = [(n² – 1) / (n² + 2)] · V_М = (4π / 3) · N_А· α_эл , (16)

 

где Р_эл – электронная поляризация вещества, R_М – мольная рефракция, V_М – мольный объем, N_А – число Авогадро, α_эл – электронная поляризуемость молекулы.

Вычитая поляризацию при высоких частотах, найденную по уравнению Лоренца-Лорентца, из поляризации при низких частотах по уравнению Клаузиуса-Моссотти, можно определить ориентационную составляющую общей поляризации:

 

Р_ор = (4π / 3) · N_А · (μ_с² / 3kT), (17)

 

а затем вычислить дипольный момент молекулы μ_с.

 

Экспериментальная часть.

Цель работы - определение дипольного момента молекулы аце­тона, используя метод разбавленных растворов.

Для этого измеряют емкости конденсаторов с раст­ворами ацетона в четыреххлористом углероде и определяют показатель преломления ацетона и четыреххлористого углерода.

Приборы и реактивы:

1. Измеритель емкости.

2. Стеклянные сосуды, в которых находятся плоские конденсаторы, погруженные в растворы ацетона в четыреххлористом углероде.

3. Рефрактометр Аббе.

4. Растворы ацетона в четыреххлористом углероде (концент­рации растворов даны в мольных долях, например, 0,01; 0,02 и т.д.). Чис­тые вещества: (СН₃)₂ СО, CCl₄.

5. Фильтровальная бумага, фланель.

Порядок выполнения работы.

 

1. Используя методические указания, под руководством лаборанта озна­комиться с работой на приборах.

2. Измерить емкости конденсаторов, заполненных растворами ацетона с концентрацией Х₂ (мольная доля) в неполярном растворителе с концентрацией Х₁ (мольная доля).

3. Измерить показатели преломления чистых ацетона n₂ и четыреххлористого углерода n₁ на рефрактометре Аббе.

4. Рассчитать диэлектрическую проницаемость изучаемых раст­воров e ацетона в четыреххлористом углероде по формуле:

 

(e₁ – 1)·(С_х – С_о)

e = 1 + ¾¾¾¾¾¾—, (18)

С₁ – С_о

 

где e₁ = 2,23 – диэлектрическая проницаемость четыреххлористого углерода;

С_х – емкость конденсатора с раство­ром полярного вещества (ацетона) в неполярном растворителе (четыреххлористом углероде);

С_о - емкость "пустого" (без жидкости) конденсатора;

С₁ - емкость конден­сатора, наполненного чистым растворителем (четыреххлористым углеродом).

5. Полученные экспериментальные данные занести в таблицу 6.

 

Таблица 6.

 

Конден- сатор	X2	X1	r, г/см^3	Со, пФ	С1, пФ	Сх, пФ	e
№1	0,01	0,99	1,588
№2	0,03	0,97	1,574
№3	0,06	0,94	1,557
№4	0,10	0,90	1,532

Обработка результатов.

1. Выражение для мольной поляризации раствора полярного вещества (ацетона) в неполярном растворителе (четыреххлористом углероде):

e – 1

Р_м = ¾¾ × V_М = X₁ (Р_1эл + Р_1ат) + X₂ (Р_2эл + Р_2ат + P_2op), (19)

e + 2

где e – диэлектрическая проницаемость раствора;

V_М – мольный объем раствора, [см ³/ моль];

X₁– концентрация раство­рителя,

X₂ – концентрация растворенного вещества в мольных долях:

(Х₁ + Х₂ = 1);

Р_1эл и Р_2эл – мольные электронные поляри­зации растворителя и растворенного вещества;

Р_1ат и Р_2ат – мольные атомные поляризации компонентов раствора (их значениями можно пренебречь, поскольку они невелики по сравнению с элект­ронной поляризацией Р_ат ≪ Р_эл), вычислить мольную ориентационную поляризацию [см³/моль] растворенного вещества по уравнению:

 

 

1 ì e – 1 ü

P_op = ¾ · í ¾¾ × V_М – Х₁Р_1эл – Х₂ Р_2эл ý. (20)

X₂ î e + 2 þ

 

2. Мольные объемы растворов V_М рассчитываются по уравнению:

 

V_М = (1/r)(Х₁М₁+ Х₂М₂), (21)

 

где М₁, М₂ - соответственно, мольные массы ацетона и четыреххлористого углерода, г/моль; r - плотность раствора, г/см³.

Электронные поляризации компонентов раствора находятся по уравнениям:

 

n²₁ – 1 n²₂ – 1

Р_1эл = ¾¾¾ × V_М1 ; Р_2эл = ¾¾¾ × V_М2 . (22)

n²₁ + 2 n²₂ + 2

 

Здесь V_М1= М₁/r₁ и V_М2= М₂/r₂ – это мольные объемы четыреххлористого углерода и ацетона, r₁ и r₂ - их плотности, соответственно.

 

Таблица 7.

 

Растворитель ССl4	Растворенное вещество, (СН3)2СО
М1 = г/моль	М2 = г/моль
r1 = г/см ^3	r2 = г/см ^3
VМ 1 = см^3/моль	VМ 2 = см^3/моль
n1 =	n2 =
Р1эл= см^3/моль	Р2эл = см^3/моль
e1 = 2,23	e2 = 21,50

 

Рассчитанные величины представить по приведенной форме, заполнив таблицы 7 и 8.

3. Построить график зависимости Р_ор от вели­чины 1/V_М, а затем аппроксимировать ее прямой линией (примерный вид его показан на рис.6.). При этом необходимо из точки 1/V_М = 1/V_М1 на оси абсцисс (V_М1 - мольный объем чистого растворителя) провести ось ординат (P_op).

Затем зависимость P_op от 1 / V_М экстраполировать на бесконечное разбавление (провести прямую Р_ор= f (1/V_М) до пере­сечения с осью Р_oр) и найти P_оp* (см. рис. 1).

4. Вычислить дипольный момент молекулы ацетона по преобразованному уравне­нию (Р_ор = μ_с² / 3kT) m= 1,28×10^-2 (P_оp* × T)^1/2, где Т - абсолютное зна­чение температуры опыта.

5. Рассчитанное значение дипольного момента сравнить с табличным (см.табл.10.).

6. Определить погрешность измерения.

 

Таблица 8.

 

Раст- воры	X2	РМ, см^3/моль	e ε	VМ, см^3/моль	10^3/VМ моль/см^3	Х1 · Р1эл см^3/моль	Х2 · Р2эл см^3/моль	Pор см^3/моль
№1	0,01
№2	0,03
№3	0,06
№4	0,10

 

Рис. 6.

Таблица 9.

 

Вещество	Формула	Молярная масса М, г/моль	Плот-ность r, г/см^3	e	n	Рефракция R, см^3/моль
Четырех-хлористый углерод	ССl4	153,81	1,595	2,23	1,460	26,51
Ацетон	(CH3 )2CO	58,08	0,791	21,4	1,359	16,15
Бензол	C6H6	78,12	0,879	2,28	1,501	26,18
Этиловый спирт	C2Н5ОН	46,07	0,789	25,2	1,361	12,78
Хлороформ	СНСl3	119,37	1,498	4,72	1,446	21,25

 

n - показатель преломления для желтой D -линии натрия.

 

Таблица 10.

Дипольные моменты молекул

Вещество	m, Д	Вещество	m, Д
H2O	1,84	NH3	1,46
CO2		HCl	1,03
CO	0,12	HBr	0,79
CH4		HI	0,30
CHCl3	1,15	(CH3)2CO	2,83
C6H5NO2	3,96	SO2	1,61

 

Литература.

1. Угай Я.А. Общая химия. - М, Высшая школа. 1984.

2. Карапетьянц М.Х., Дракин А.П., Строение вещества. - М.: Высшая

школа, 1989.

3. Новиков А.Ф., Успенская М.В. Электронный учебник по курсу химии,

глава 3. "Химичeскaя связь, стрoeниe и свoйствa мoлeкул", раздел 3.5.

Центр дистанционного обучения СПб.ГУИТМО, 2004.

 

 

Лабораторная работа № 4

ТЕПЛОВЫЕ ЭФФЕКТЫ ХИМИЧЕСКИХ ПРОЦЕССОВ

Теоретическая часть.

 

Термохимия - раздел химической термодинамики, предметом которой является определение тепловых эффектов химических реакций или фазовых превращений веществ экспериментальными и расчетными методами. При этом она основывается на общих законахтермодинамики .

Термодинамической системой принято называть вещество или совокуп­ность взаимодействующих веществ, мысленно или реально выделяемых в пространстве. Остальная часть пространства со всем, что в ней находится, называется окружающей средой. Система считается закрытой, если между ней и окружа­ющей средой возможен только обмен теплом. Для описания состояния термодинамической системы вводятся термодинамические параметры (объем, температура, давление, количество вещества) и термодинамические функции (внутренняя энергия, энтальпия, энтропия, энергия Гиббса и др.).

Прежде всего химическая система характеризуется термодинамическими параметрами. К термодинамическим параметрам (или переменным) системы относятся такие параметры, которые могут быть изменены или заданы извне, а именно: давление p, объем V, температура T, количество молей вещества ν, концентрация c_конц. Иногда к ним относят и количество теплоты Q, подводимое к системе извне или отводимое от нее. Основные термодинамические параметры связаны между собой известным уравнением Менделеева-Клапейрона (см. лабораторную работу №1): pV = ν · RT. Его можно преобразовать к следующему виду: p = (ν ⁄ V) · RT, а так как мольная концентрация c_конц = ν ⁄ V, то

p = c_конц · RT. (1)

 

К термодинмическим функциям относят прежде всего внутреннюю энергию U, включающую в себявсе возможные виды энергии частиц, составляющих систему, исключая кинетиче­скую и потенциальную энергии самой системы. Внутренняя энергия системы определяется энергией движения молекул, энергией дви­жущихся электронов в атомах, энергией внутримолекулярных коле­баний атомов и атомных групп, внутриядерной энергией и т.п. По этой причине абсолютное значение внутренней энергии, впрочем, как и других функций состояния, определено быть не может, однако могут быть найдены изменения этих функций в ходе превращений.

Основным законом термодинамики является закон сохра­нения энергии, который в термодинамической форме выра­жается уравнением:

DQ = DU + A. (2)

 

Это уравнение означает, что если к системе подводится теп­лота DQ, то она расходуется на изменение внутренней энергии DU и на совершение работы А. При этом:

DU = U₁ - U₂, (3)

 

где U₁ - внутренняя энергия система в начальном состоя­нии;

U₂ - внутренняя энергия системы в конечном состояний.

Под величи­ной А имеют в виду работу, совершаемую системой против сил, действующих на нее извне: внешнего давления, электрического и магнитного поля и т. д. Если на систему не действуют никакие силы, кроме сил внешнего давления, то работа про­тив сил внешнего давления выражается уравнением:

А = р × DV. (4)

 

где DV = V₂ - V₁ - изменение объема системы;

р-давление в системе.

В термодинамике оказалось удобным ввести еще одну функ­цию, характеризующую состояние системы, энтальпию Н, которая определяется следующим образом:

H = U + pV. (5)

 

Экспериментально невозможно определить абсолютное значение энтальпии и внутренней энергии системы, но можно определить количество тепла, которым обменивается система с окружающей средой, и количество совершаемой работы, поэтому в термодинамике принято учитывать только изменения термодинамических функций.

Подобно внутренней энергии изменение энтальпии DН = Н₂ - Н₁ характеризует изменение энергетического состояния системы при ее переходе из начального со­стояния в конечное:

 

DH =DU + p DV. (6)

 

Таким образом, выделение теплоты из системы или поглощение ею теплоты из окружаю­щей среды в результате химического процесса или фазового пе­рехода связывают с изменением внутренней энергии си­стемы, если процесс происходит при постоянном объеме Q_v = DU, или с изменением энтальпии, если процесс происходит при по­стоянном давлении в системе Q_р = DН.

Так как внутренняя энергия системы является функцией температуры, то тепловые эффекты процессов также зависят от температуры.

Тепловым эффектом, или теп­лотой химической реакции, называется изменение энтальпии системы в результате прохождения реакции, определяемое как количество теплоты, которое выделяется (поглощается) системой в результате необратимого химического процесса при условии постоянства давления. При этом исходные вещества и продукты реакции должны иметь одинаковую температуру. Обычно тепловой эффект реакции относят к 1 молю вещества и стандартным условиям (температура 298 К (+25^оС), нормальное атмосферное давление 101325 Па), выражают его в единицах энергии, в кДж/моль. Изменение энтальпии, отвечающее стандартным условиям, обозначают так: DН^о₂₉₈.

Если в ходе реакции запас энергии в системе повышается, система поглощает тепло, то тепловой эффект ее имеет положительное значение ΔН > 0, что соответствует эндотермической реакции, в противоположном случае говорят об экзотермической реакции: ΔН < 0. Таким образом, тепловой эффект реакции имеет знак «-», если теплота выделяется из системы (экзотермическая реакция), и знак «+», если теплота поглощается системой (эндотермическая реакция).

Уравнения химических реакций, в которых указывается тепловой эффект химических реакций, получили название термохимических уравнений. В термохимических уравнениях тепловой эффект химической реакции записывается рядом с уравнением баланса масс. При этом указывается также агрегатное состояние веществ.

Например:

Н_{2 газ} +1/2 О_{2 газ} → Н₂О_жидк ; DН°₂₉₈ = -285,5 кДж/моль. (7)

 

В термохимии в качестве одной из стандартных характеристик индивидуальных веществ является тепловой эффект, или энтальпия образования, одного моля химического соединения из простыx веществ. При этом условно принимается, что энтальпия образования простых веществ равна нулю (DН°_f = 0).

При расчетах тепловых эффектов реак­ций с участием органических веществ часто используются величины теплот сгорания моля вещества в кислороде с образованием углекислого газа СО_{2 газ} и воды Н₂О_жидк при стандартных условиях. Их обозна­чают как DН°_сгор.

 

Законы термохимии .

 

Термохимия как экспериментальная часть химический термодинамики базируется на двух основных законах.

Первый закон термохимии (закон Лавуазье-Лапласа) формулируется так: Тепловой эффект реакции образования сложного вещества из простых равен по абсолютному значению, но противоположен по знаку тепловому эффекту реакции разложения данного соединения на простые вещества. Таким образом,

 

ΔНº_обр = –ΔНº_разл. (8)

 

Или, обобщая: Тепловой эффект прямой реакции равен тепловому эффекту обратной реакции, но с противоположным знаком. Этот закон часто применяют тогда, когда невозможно или трудно определить опытным путем тепловой эффект, скажем, прямой реакции, но легко определить его для обратной реакции.

Второй закон термохимии (закон Гесса) формулируется следующим образом:

Тепловой эффект химической реакции, протекающей при постоянном давлении или при постоян­ном объеме, не зависит от числа, последовательности и характера ее промежуточных стадий, но определяется только природой исходных веществ и продуктов и условий реакции, а также начальным и конечным состоянием системы.

 

Запись закона: ΔН_реакц = ΔН_ст1 + ΔН_ст2 + ΔН_ст3 + ΔН_ст... (9)

 

Закон Гесса дает возможность вычислить тепловой эффект процесса. Он используется для расчета DН, DU реакции, а также в том случае, когда процесс либо экспериментально не проводится, либо не может быть осуществлен вообще.

Рассмотренные определения дают возможность сформули­роватьдва важных следствия из закона Гесса.

Первое следствие: Тепло­вой эффект реакции равен сумме теплот образования продуктов реакции за вычетом суммы теплот образования исход­ных веществ с учетом стехиометрических коэффициентов в уравнении реакции.

Например, для реакции n₁А + n₂В → n₃С + n₄D можно записать:

 

DНº = (n₃DНº_С + n₄DНº_D) - (n₁DНº_A +n₂DНº_B). (10)

Или в общем виде: ΔН_х.р = Σn_j·ΔНº_обр^прод – Σn_i·ΔНº_обр^реаг_, (11)

 

где n_j и n_i - стехиометрические коэффициенты при химических символах продуктов и реагентов в уравнении реакции.

Второе следствие: Тепловой эффект химической реакции с участием органических веществ равен сумме теплот сгорания исходных веществ за вычетом суммы теплот сгорания продуктов реак­ции с учетом стехиометрических коэффициентов.

Например, для реакции n₁А + n₂В → n₃С + n₄D можно записать:

DНº = (n₁DНº_A +n₂DНº_B) - (n₃DНº_С + n₄DНº_D). (12)

Или в общем виде: ΔНº_х.р = Σn_i·ΔНº_сгор^реаг – Σn_j·ΔНº_сгор.^прод . (13)

 

Практически для расчета теплового эффекта химической реакции необходимо написать уравнение этой реакции и привести для каждого из участвующих в реакции веществ значение стандартной теплоты его образования или сгорания.

Зависимость теплового эффекта реакции от температуры может быть выражена через изменение теплоемкости системы в результате прохождения химиче­ского процесса или фазового превращения. Изменение теплоемкости для процесса при постоян­ном давлении может быть записано так:

 

DС_Р