
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постулати Бота. Спектр атома водню по БоруСодержание книги
Поиск на нашем сайте
Перша спроба побудови якісно нової теорії атома була зроблена в 1913 р. Н. Бором. Він поставив перед собою мету зв’язати в єдине ціле емпіричні закономірності лінійчастих спектрів, ядерну модель атома Резерфорда і квантовий характер випромінювання та поглинання світла. Теорія Бора застосовна до атома водню і воднеподібної системи, яка складається із ядра з зарядом В основу своєї теорії Бор поклав три постулати. Перший постулат Бора (постулат стаціонарних станів): існують деякі стаціонарні стани атома з відповідними значеннями енергії Цим стаціонарним станам відповідають цілком визначені (стаціонарні) орбіти, по яких рухаються електрони, які, незважаючи на наявність у них прискорення, електромагнітних хвиль не випромінюють. Другий постулат Бора (правило квантування орбіт): в стаціонарному стані атома електрон, рухаючись по коловій орбіті, повинен мати квантові значення моменту імпульсу, які задовольняють умову де Третій постулат Бора (правило частот): при переході атома з одного стаціонарного стану в інший випромінюється або поглинається один фотон з енергією Випромінювання фотона відбувається при переході атома зі стану з більшою енергією Постулати, висунуті Бором, дозволили розрахувати спектр атома водню і воднеподібних систем, а також теоретично розрахувати сталу Рідберга. Враховуючи припущення Резерфорда, що електрон у воднеподібній системі рухається по коловій орбіті радіусом r під дією кулонівської сили притягання електрона до ядра, яка створює доцентрове прискорення, запишемо: Підставивши сюда величину де Радіуси орбіт зростають пропорційно квадратам цілих чисел.
Енергія електрона у воднеподібній системі дорівнює сумі його кінетичної і потенціальної енергій в електростатичному полі ядра: Знак “–“ означає, що електрон знаходиться у зв’язаному стані. Енергетичні стани атома утворюють послідовність енергетичних рівнів, що змінюються залежно від значення n, яке виражає номер енергетичного рівня атома. Надаючи n різні цілочислові значення, отримаємо для атома водню (Z = 1) можливі рівні енергії (рис. 168).
Енергія атома водню із збільшенням n зростає (зменшується її від’ємна величина), і енергетичні рівні наближаються до границі, що відповідає значенню Згідно з третім постулатом Бора звідки частота випромінювання де Теорія Бора не позбавлена внутрішніх протиріч (з одного боку, застосовує закони класичної фізики, з іншого, – ґрунтується на квантових постулатах). Вона змогла пояснити спектри водню і водневоподібних систем і обчислити частоти спектральних ліній, але не змогла пояснити їх інтенсивність і не дала відповіді на запитання: чому здійснюються ті чи інші переходи? У теорії Бора не описано атом гелію – один з простих атомів, що безпосередньо слідує за атомом водню.
4. Гіпотеза Луї де Бройля. Корпускулярно-хвильовий дуалізм матерії; Як показано в розділі 6, світло володіє як хвильовими, так і корпускулярними властивостями. Луї де Бройль (1924 рік) висунув гіпотезу (постулат) про те, що корпускулярно-хвильовий дуалізм притаманний не тільки світлу, але матерії взагалі: усяка частинка, яка має імпульс
та частотою
В залежності від величини швидкості v (кінетичної енергії
або за релятивістською формулою (при
де m – маса частинки (таблична величина), Зокрема, вільна частинка, що рухається вздовж осі х, описується плоскою хвилею де Бройля
де
а групова швидкість
Борівське квантування моменту імпульсу орбітального руху електрона набуває нового змісту з врахуванням хвильових властивостей електрона. Зокрема, довжина стаціонарної орбіти
тобто в межах орбіти вкладається ціле число хвиль де Бройля. Оцінимо довжину хвилі де Бройля електрона, який прискорився електричним полем Відомо, що найбільш чітко хвильові властивості світла проявляються в явищі дифракції. І тому прояв хвильових властивостей електронних (нейтронних, атомних тощо) пучків слід очікувати в цьому ж явищі. При цьому чітка дифракційна гратка спостерігається тоді, коли довжини хвиль співмірні з розміром дифракційної неоднорідності (отвори, щілини тощо). Розміри макроприладів значно перевищують довжини хвиль де Бройля електронів, і тому в цьому випадку хвильові властивості електронів явно не відслідковуються. В цей же час розраховані значення l співмірні з розміром (
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.109.60 (0.01 с.) |

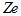 і одного електрона, що обертається навколо ядра:
і одного електрона, що обертається навколо ядра:  ,
,  ,….
,…. перебуваючи в яких, він не випромінює енергії.
перебуваючи в яких, він не випромінює енергії. ,
, – маса електрона,
– маса електрона,  – його швидкість,
– його швидкість,  – радіус орбіти електрона.
– радіус орбіти електрона.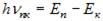 , яка дорівнює різниці енергій відповідних стаціонарних станів.
, яка дорівнює різниці енергій відповідних стаціонарних станів. у стан з меншою енергією
у стан з меншою енергією  , тобто при переході електрона з орбіти більш віддаленої від ядра на ближчу до ядра орбіту. Поглинання енергії супроводжується переходом атома у стан з більшою енергією, і електрон переходить на віддаленішу від ядра орбіту. Набір можливих частот
, тобто при переході електрона з орбіти більш віддаленої від ядра на ближчу до ядра орбіту. Поглинання енергії супроводжується переходом атома у стан з більшою енергією, і електрон переходить на віддаленішу від ядра орбіту. Набір можливих частот  квантових переходів і визначає лінійчастий спектр атома.
квантових переходів і визначає лінійчастий спектр атома.
 з виразу
з виразу  , отримаємо:
, отримаємо: і
і  ,
,
 .
.
 . Атом водню має мінімальну енергію
. Атом водню має мінімальну енергію  при n=1 і максимальну
при n=1 і максимальну  при
при  .
. ,
,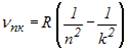 ,
, . Значення
. Значення  . Це підтверджує правильність отриманої Бором формули для енергетичних рівнів водневоподібної системи.
. Це підтверджує правильність отриманої Бором формули для енергетичних рівнів водневоподібної системи.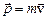 і енергію Е, володіє хвильовими властивостями, її рух супроводжується хвильовим процесом з довжиною хвилі де-Бройля
і енергію Е, володіє хвильовими властивостями, її рух супроводжується хвильовим процесом з довжиною хвилі де-Бройля (7.11)
(7.11) . (7.12)
. (7.12) ) частинок, їх імпульс розраховується або за класичною формулою (при
) частинок, їх імпульс розраховується або за класичною формулою (при  )
) , (7.13)
, (7.13) , Еk співмірна з Е 0)
, Еk співмірна з Е 0) , (7.14)
, (7.14) – її енергія спокою.
– її енергія спокою. , (7.15)
, (7.15) – амплітуда хвилі де Бройля,
– амплітуда хвилі де Бройля,  – її циклічна частота,
– її циклічна частота,  – її хвильове число. Фазова швидкість хвиль де Бройля
– її хвильове число. Фазова швидкість хвиль де Бройля
 , (7.16)
, (7.16)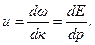 (7.17)
(7.17) ,
, . Саме такі напруги використовуються у вакуумних електронних приладах (радіолампи, ЕПТ, рентгенівські трубки тощо). Підставляючи в формулу (7.13) значення кінетичної енергії електронів
. Саме такі напруги використовуються у вакуумних електронних приладах (радіолампи, ЕПТ, рентгенівські трубки тощо). Підставляючи в формулу (7.13) значення кінетичної енергії електронів  е В, отримаємо за (7.11) для довжин хвиль де Бройля
е В, отримаємо за (7.11) для довжин хвиль де Бройля  нм.
нм. нм) кристалічної гратки твердих тіл. І тому така гратка повинна бути дифракційним пристроєм для електронних пучків. Дійсно, при проходженні електронних пучків через тонкі полікристалічні плівки та при їх відбиванні від монокристалів спостерігається така ж дифракційна картина, як і при взаємодії рентгенівських променів з твердими кристалічними тілами. Зокрема, виконується закон Вульфа-Бреггів (див. розділ 6), встановлений для рентгенівських променів. Дифракція нейтронних пучків також виявлена експериментально і використовується для наукових досліджень.
нм) кристалічної гратки твердих тіл. І тому така гратка повинна бути дифракційним пристроєм для електронних пучків. Дійсно, при проходженні електронних пучків через тонкі полікристалічні плівки та при їх відбиванні від монокристалів спостерігається така ж дифракційна картина, як і при взаємодії рентгенівських променів з твердими кристалічними тілами. Зокрема, виконується закон Вульфа-Бреггів (див. розділ 6), встановлений для рентгенівських променів. Дифракція нейтронних пучків також виявлена експериментально і використовується для наукових досліджень. Відмітимо, що довжини хвиль де Бройля макроскопічних тіл, за рахунок великої маси, настільки малі, що їх хвильові властивості виявити неможливо.
Відмітимо, що довжини хвиль де Бройля макроскопічних тіл, за рахунок великої маси, настільки малі, що їх хвильові властивості виявити неможливо.


