
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I – угол падения, r – угол преломленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
I – угол падения, r – угол преломления 6. В дно водоёма глубиной 2,0 м вбита свая, на 0,75 м выступающая из воды. Найти длину тени от сваи на поверхности и на дне водоёма, если высота солнца над горизонтом в данный момент равна 45º. . tg45 = h/l=>l = h/tg45 = h= 0,75 м, В некоторую точку пространства приходят два пучка когерентного излучения с оптической разностью хода 2,0 мкм. Определить, произойдет усиление или ослабление в этой точке света с длиной волны 400 нм. Переведем 2,0 мкм = 2*10-6 м, 400 Нм = 400 * 10-9 м Из условия максимума: ∆S= mλ, тогда m = ∆S/λ = 2*10-6 / 400*10-9 = 10-6/ 2 * 10-7 = 10/2= 5. т.к. m – целое число, то произойдет усиление. В опыте Юнга отверстия освещались монохроматическим светом длиной волны l = 6·10-5 см, расстояние между отверстиями 1 мм и расстояние от отверстий до экрана 3 м. Найдите положение первой светлой полосы. Первая светлая полоса находится на растоянии y1=(L/d)λ=1.8*10-3 м. Вторая – на растоянии y2=2y1=3.6*10-3 м. Третья- на растоянии y3=3y1=5.4*10-3 м. В опыте Юнга на пути одного из интерферирующих лучей помещалась тонкая стеклянная пластинка. Вследствие чего центральная светлая полоса смещалась в положение, первоначально занятое пятой светлой полосой (не считая центральной). Луч падает перпендикулярно к поверхности пластинки. Показатель преломления пластинки 1,5, длина волны 600 Нм. Какова толщина пластинки. ∆S=2d (n-1)= mλ. При m=5. ответ: 1200*10-9 м. или 1,2 мкм Во сколько раз изменится ширина интерференционных полос на экране в опыте Юнга, если фиолетовый светофильтр (0,4 мкм) заменить красным (0,7 мкм)? ∆х= l/d * λ0. чертеж. Трофимова 324. Т.к. расстояния от щели до экрана и между щелями мы не меняем, а меняем только светофильтры, то тогда ∆х = λ1/ λ2 получим в 0,6 мкм. В чем заключается принцип Гюйгенса?
2. В чем заключается метод зон Френеля?Разбиение волновой поверхности S на зоны, границы первой (центр) зоны служат точки поверхности S наход на расстоянии l+λ\2 от точки M. Точки сферы наход на расстоянии l+2λ\2, l+3λ\2 от точки M, образ зоны Френеля. При наложении этих колебаний они взаимно ослаб друг друга A=A1-A2+A3-A4…+Ai С увелич номера зоны,уменьш интенсивность излучения зоны в насправлении т.M, т.е уменьш Ai A1>Ai>A3…>Ai 3. Вычислите радиус пятой зоны Френеля для плоского волнового фронта, если точка наблюдения находится на расстоянии 1 м от фронта волны. Длина волны равна 0,5 мкм. Расстояние от внешнего края k-ой зоны Френеля до т наблюд R равно bk=b+k *λ/2. Rк 2 +b2 = (b+k *λ/2)2 . Rк 2 +b2 = b2 +bkλ+ k2 *λ2/4; Rк 2 = bkλ+ k2 *λ2/4; k2 *λ2/4 можно пренебречь. R5=√(bkλ)=>r5=1.58 мм В чём заключается явление двойного лучепреломления? Двойным лучепреломлением обладают все прозрачные кристаллы, т.е. раздваивание каждого падающего на них светового пучка. Способность веществ расщеплять падающих световой луч на 2 луча – обыкновенный и необыкновенный, которые распространяются в различных направлениях с различной фазовой скоростью и Исландского шпата направить узкий пучок света, то из кристалла выйдут два пространственно разделенных луча, параллельных друг другу и падающему лучу. Когда первичный пучок падает на кристалл нормально, преломленный пучок разделяется на два, причем один из них является продолжением первичного, а второй отклоняется. Второй из них получил название необыкновенного, а первый-обыкновенный. В каком случае при прохождении света через анизотропный кристалл не будет наблюдаться двойного лучепреломления? При прохождении через оптическую ось кристалла. Свет падает нормально на плоскую поверхность оптически отрицательного одноосного кристалла, оптическая ось которого параллельна ей. Оптическая ось лежит в ней. В этом случае необыкновенный луч не преломляется, а совпадает по направлению с падающим и обыкновенным.
Во сколько раз ослабляется свет, проходя через два николя, плоскости поляризации которых составляют угол 300, если в каждом из николей в отдельности теряется 10% падающего на него светового потока? K=0,1 I2/I0 = [I0 (1-k) cos2α (1-k)2]/2 I0 = в 0,3 раза 1. Во сколько раз надо увеличить абсолютную температуру АЧТ, чтобы его энергетическая светимость возросла в 9 раз?
2. Вследствие изменения температуры абсолютно черного тела максимум спектральной плотности энергетической светимости сместился с 2,4 мкм на 0,8 мкм. Как и во сколько раз измен-сь энергетич. светимость тела?
3. Вычислить истинную температуру вольфрамовой раскаленной нити, если радиационный пирометр показывает температуру 2,5 кК. Принять, что поглощательная способность для вольфрама 0,35.
Монохроматический пучок света с длиной волны 490 нм, падая по нормали к поверхности, производит световое давление 4,9 мкПа. Какое число фотонов падает в единицу времени на единицу площади этой поверхности? Коэффициент отражения света 0,25.
Молярная теплоемкость молибдена при температуре 20 К равна 0,6 Дж/(моль·К). Вычислить характеристическую температуру Дебая. Условие T<<QD считать выполненным, теплоемкость в предельном случае Дано: Сm=0,6 Дж/(моль·K) Т=20 К T<<QD Найти: ΘD=? Решение: Сm=234R(T/ ΘD)3 ΘD= 234·R(T3)/ Сm ΘD=(25927,2)1/3 K [(Дж·К·моль·К)/(моль 12. На какую максимальную глубину нужно поместить точечный источник света, чтобы квадратный плот со стороной 4 м не пропустил ни одного луча в пространство над поверхностью воды? Центр плота находится над источником света. Показатель преломления воды n = 1,33. sinα=1/1.33; α=48.6; h=tgα/2=0.567 м 13. Над центром круглой площадки висит лампа. Освещенность в центре площадки Е 0 = 40 лк, на краю площадки Е = 5 лк. Под каким углом падают лучи на край площадки? E=E0cosa=(I/h2)cosa 14. Над центром круглого стола радиусом 80 см на высоте 60 см висит лампа силой света I =100 кд. Опред-ть освещенность Е 0 в центре стола. Прямоуг треугольник, левый катет 6 м, нижний катет r= 8м. Гипотенуза по теореме Пифагора 10 м; E=Icos2 0/r=100/8=12,5 м 15. Над центром круглого стола радиусом 80 см на высоте 60 см висит лампа силой света I =100 кд. Определить освещенность Е на краю стола. Прямоуг треугольник, левый катет 6м, нижний катет r= 8 м. Гипотенуза по теореме Пифагора 10 м, tga=2/3≈30 градусов, E=Icos2 30/r=75/16 = 4,7 м На стеклянную пластинку нанесен тонкий слой прозрачного вещества, с показателем преломления n = 1,3. Пластинка освещена параллельным пучком света монохроматического света, с длиной волны l = 640 нм, падающим на пластинку нормально. Какую наименьшую толщину dmin должен иметь слой? Чтобы отраженный пучок имел наименьшую яркость? Λ=640*10-9 м. Условие минимума: 2d√n2-sin20+ λ\2 = (2m+1)λ\2 2dn + λ\2 = (2m+1)λ\2. При m = 1 Ответ: 246,2*10-9 На мыльную плёнку (n = 1,3) падает нормально пучок лучей белого света. Какова наименьшая толщина плёнки, если в отражённом свете она кажется зелёной (l = 550 нм)? Λ=550*10-9 м. Условие максимума: 2d√n2-sin20+ λ\2 = mλ. 2dn + λ\2 = mλ. При m=1. Ответ: 105,8*10-9 На мыльную плёнку (n = 1,3) падает белый свет под углом 45º. При какой наименьшей толщине плёнки отражённые лучи будут окрашены в жёлтый (l = 6·10-5 см) цвет?
По условию отраженные лучи отражены в желтый цвет. Это означает, что максимум отражения наблюдается в желтой части спектра. Максимум отражения наблюдается, когда световые волны отраженные от обеих поверхностей пластинки усиливают друг друга. Для этого оптическая разность хода ∆d пучков 1 и 2 должна быть равна целому числу k длин волн: ∆d=(λ/2)+n(AB+BC)-AD=kλ. слагаемое λ/2 учитывает что при отражении пучка 1 от оптически более плотной среды фаза колебаний электромагнитного поля изменяется на противоположную, т.е. возникает такое же изменение фазы, как при прохождении пути λ/2. Множитель n учитывает уменьшение скорости света в среде- на пути s в среде возникает такое же изменение фазы ∆φ, как на пути ns в вакууме: ∆φ=(ωs)/ν=(nωs)/c. Используя соотношения AC=BC=h/(cosr), AD=2hsini*tgr, a также применяя закон преломления, получаем (k-(1/2))λ=2h√(n2-sin2i), откуда h=((k-(1/2))λ)/(2√(n2-sin2i)). При k=1 минимальная толщина пленки h=0.13*10-6 м. 9. На щель падает нормально параллельный пучок монохроматического света с длиной волны l. Ширина щели равна 6l. Под каким углом будет наблюдаться третий дифракционный минимум спектра? dsinφ=kλ, по условию а=6λ, к=3, отсюда 6λsinφ=3λ; sinφ=0,5; φ=30˚ 10. На дифракционную решетку нормально падает пучок света от разрядной трубки, наполненной гелием. На какую линию в спектре третьего порядка накладывается красная линия гелия (l = 6,7·10-5 см) спектра второго порядка? dsinφ=kλ1; dsinφ=3λ2, отсюда λ2 = 2/3 λ =447 нм – синяя линия спектра гелия 11. Найти наибольший порядок спектра для жёлтой линии натрия λ = 5890Å, если постоянная дифракционной решетки d = 2 мкм. Из формулы дифрак решетки dsinφ=kλ, найдем к= dsinφ/λ. Поскольку sinφ≤1, то к≤d/λ=3,4, т.е. k max = 3 12. На щель шириной 0,1 мм нормально падает параллельный пучок света от монохроматического источника с λ = 0,6 мкм. Чему равна ширина центрального максимума в дифракционной картине, проецируемой с помощью линзы, находящейся непосредственно за щелью, на экран, отстоящий от линзы на расстоянии L = 1 м? λ=0.6 мкм=6*10-7 м, l=1м,m=1, а=0,1мм=10-4м, b-? Решение: min=аsinφ=± m λ, m=1; sinφ= λ /а; sinφ ≈tgφ; b=2ltgφ≈2lλ/a=1.2см 18. Найдите массу фотона красного света с длиной волны На металлическую пластинку с работой выхода hν=Aвых+E. Е= hν-Aвых =0,004 *10-19Дж. h=6,62*10-34 Дж*с. Наибольшая длина волны света, при которой может наблюдаться фотоэффект для калия, равна
красная граница фотоэффекта:λкр=(hc)/A откуда работа выхода электронов: A=(hc)/λкр=(6.62*10-34*3*108)/6.2*10-7=3.2*10-19 Дж На поверхность металла падает монохроматический свет с длиной волны 0,1 мкм. Красная граница фотоэффекта 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии? На фотоэлемент с катодом из лития падает свет с длиной волны 200 нм. Найти наименьшее значение задерживающей разности потенциалов, которую нужно приложить к фотоэлементу, чтобы прекратить фототок.
Найти длину волны фотона при переходе электрона из состояния с энергией (–5 эВ) в состояние с энергией (–9 эВ). 2-ой постулат Бора так как 20. На сколько изменится энергия электрона в атоме водорода при излучении атомом фотона с длиной волны Согласно второму постулату Бора частота излучения, соответствующая переходу электрона с одной орбиты на другую, определяется формулой где с=3*108 м/с – скорость света, Найти длину волн де Бройля для электрона, имеющего кинетическую энергию
Найти длину волны де Бройля для шарика массой 1г, движущегося со скоростью 10 м/с. Найти толщину слоя половинного ослабления для рентгеновских лучей. Линейный коэффициент поглощения равен 1,4·103 м-1. Дано: μ=1,4·103 м-1 Найти: х1/2=? Решение: х1/2=ln2/μм·ρ μм= μ/ρ х1/2=ln2/μ x1/2=0,495·10-3[1/м-1]=0,5 мм Найти среднюю продолжительность жизни атома радиоактивного изотопа кобальта 6027Со. λ= ln2/T1/2=0,131 г T1/2= 5,3 г τ=1/λ=7,646 г 13. Определите радиус четвертой зоны Френеля, если радиус второй зоны Френеля для плоского волнового фронта равен 2 мм. M1=2,м2 =4, r1=2 мм=2*10-3 м, r2-? Решение: r2 +b2 = (b+k *λ/2)2 ; R2 = bmλ+m2λ2/4; λ<<b; r=√bmλ; r1/r2=√m1/m2; r2=r1√m2/m1=2.83мм 14. Определите постоянную дифракционной решетки, если она в первом порядке разрешает две спектральные линии калия (l1 = 578 нм и l2 = 580 нм). Длина решетки 1 см. λ 1= 578 нм=5,78*10-7 м, λ2=580*10-7 м, l=1 cm=10-2 м? d-? Решение: R=λ1/δλ=mN; N=λ1/δλm; δλ=λ2-λ1; d=1/N=lδ λm/λ1; d=34.6мкм 21. Определить диаметр нити накала электрической лампы, если мощность электрического тока, питающего лампу, равна 1000 Вт, длина нити 10 см, температура 3000 К. Считать, что излучение нити соответствует излучению АЧТ.
22. Опр-ть температуру и энергетич. светимость абсолютно черного тела, если максимум энергии излучения приходится на длину волны 600 нм.
23. Определить импульс фотона красного излучения, длина волны которого 720 нм. импульс фотона: p=h/λ=6.62*10-34/720*10-9=0.0092*10-25 (Дж*с)/м 24. Определите длину волны фотона, энергия которого равна кинетической энергии электрона, прошедшего из состояния покоя ускоряющую разность потенциалов 3,3 В. eU=(meυ2)/2 откуда υ=корню из ((2eU)/me). Энергия электрона: εe=mec2. ε=εe Энергия фотона:ε=hν=(hυ)/λ, откуда λ=(hυ)/ε=((корень из((2eU)/me))/ mec2)*h =0,087*10-13 м. 25. Опр. частоту кол-й свет.волны, масса фотона кот. равна
Масса фотона:m=(hν)/c2 откуда частота колебаний световой волны:ν=(mc2)/h, ν=(3.31*10-36*(3*108)2)/6.62*10-34=4.5*1014 Гц 26. Определить импульс фотона излучения с частотой 3×1015 Гц.
Определите, как и во сколько раз изменится мощность излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с l1=720 нм до l2=400 нм. λmax=C’/T-по первому закону Вина T=λmax/C’ Мощность излучения черного тела: P=Re*S=σT4*S Где σ- постоянная Стефана – Больцмана. P2/P1=(σT24S)/(σT14S)= T24/ T14=λ14/λ24=269/25.6=10.5 Определите длину волны де Бройля для нейтрона, движущегося со средней квадратичной скоростью при Т = 290 К.
Определите неопределенность скорости электрона, если его координата установлена с точностью до 10-5 м.
Образец магния массой 50 г нагревается от 0 до 20 К. Определить теплоту, необходимую для нагревания. Принять характеристическую температуру Дебая для магния 400 К и считать условие T<<QD выполненным. Решение: Сm=234R(T/ ΘD)3 с= Cm/М Q=c·m·ΔT m=50·10-3кг Сm=0,243 Дж/(моль·К) суд=0,0101 (Дж·моль)/(моль·К·кг)=0,0101 Дж/(К·кг) Q=10,128·10-3 Дж [(Дж·кг·К)/(К·кг)]=Дж (М(Mg)=24 кг/моль) Определите ширину запрещенной зоны собственного полупроводника, если при температурах Т1 и Т2 его сопротивления соответственно равны R1 и R2. k=1,38·10-23 Дж/К Найти: ∆Е=? Решение: При условии, что Т2 > T1 γ=γ0·e-∆E/kT γ=1/ρ R~ρ γ~1/R γ2/γ1=R1/R2 γ2/γ1=exp[-∆E/(2k·T2)]/exp[-∆E/(2k·T1)]=exp[(∆E/2k)(1/T1-1/T2)]=R1/R2 ∆E=2k [T1·T2/(T2-T1)]lnR1/R2 16. Под стеклянной пластинкой толщиной d =15 см лежит маленькая крупинка. На каком расстоянии l от верхней поверхности пластинки образуется ее видимое изображение, если луч зрения перпендикулярен к поверхности пластинки, а показатель преломление стекла n =1,5? Рисунок ж tga=AB/h; tgb=AD/H; tga/tgb=H/h; sina/sinb=H/h; h=H/h=15/1.5=10 cм 17. Предельный угол полного внутреннего отражения на границе стекло-жидкость i пр = 65º. Определите показатель преломления жидкости, если показатель преломления стекла равен 1,5. iпр =65; nc =1.5 n-? Решение siniпр=nж/nс; nж=n*siniпр; nж=1.36 15. Постоянная дифракционной решётки в 4 раза больше длины световой волны монохроматического света, нормально падающего на ее поверхность. Определить угол между двумя первыми симметричными дифракционными максимумами. d=4l, dsinj=kl=>sinj=(kl)/d=(kl)/(4l)=1/2=>j=300 16. Постоянная дифракционной решетки d = 2·10 –6 м. Какую наибольшую длину волны можно наблюдать в спектре этой решетки? Дано d= 2·10 –6 м, λ-? Решение: условие максимума dsinφ=mλ, λ=dsinφ/m, берем первый порядок и синус максимальный =>λ= 2·10 –6*1 / 1=2·10 –6 м 17. При падении света с длиной волны 0,5 мкм на дифракционную решетку третий дифракционный максимум наблюдается под углом 30º. Чему равна постоянная дифракционной решетки? dsinφ=mλ; λ=0.5мкмһ5*10-7м, m=3, sinφ=30. решение d= mλ/ sinφ=30*10-7 18. Постоянная дифракционной решетки d = 2·10 –6 м. Какой наибольший порядок спектра можно видеть при освещении её светом длиной волны 1 мкм? λ=1 мкм=10-6 м dsinφ=mλ; m= dsinφ/λ=2 Параллельный пучок света переходит из глицерина в стекло так, что пучок, отражённый от границы раздела этих сред, оказывается максимально поляризованным. Определить угол между падающим и преломлённым пучками. Абсолютные показатели преломления глицерина и стекла 1,45 и 1,5 соответственно. 1.5/1.45=1.07=tgα(следует)α=arctg1.07= 470 –падающий луч sin47/1.07=0.68 arcsin0.68=430 – преломленный луч Пластинку кварца толщиной d = 2 мм поместили между параллельными николями, в результате чего плоскость поляризации монохроматического света повернулась на угол a = 45o. Какой наименьшей толщины d min следует взять пластинку, чтобы поле зрения поляриметра стало совершенно тёмным? Угол поворота равен: φ= αd.(для кристаллов и прозрачных веществ). Поле будет темным при φ= 900 Значит, нам необходимо повернуть пластинку еще на 450 , для того, чтобы они были взаимно перпендикулярны. Тогда d min=d+d. Ответ: 4 мм. 27. При какой температуре максимум спектральной плотности энергетической светимости абсолютно чёрного тела приходится на длину волны 0,642 мкм? λmax=C’/T-по первому закону Вина. Где C’-первая постоянная Вина. T=λmax/C’=0,642*10-6/2,898*10-3=0,22*10-3 K 28. При какой температуре энергетическая светимость абсолютно черного тела равна 1 Вт/м2?
29. Площадь, ограниченная графиком спектральной плотности энергет. светимости черн. тела, при переходе от темп-ры Т1 к темп-ре Т2 увеличилась в 16 раз. Во сколько раз возросла темп-ра?
30. Поток энергии, излучаемой из смотрового окошка плавильной печи, равен 34,6 Вт. Опр-ть температуру печи, если площадь отверстия 6,1 см2.
31. Поток излучения абсолютно черного тела 10 кВт. Максимум энергии излучения приходится на длину 0,8 мкм. Определить площадь излучающей поверхности.
Плоская вольфрамовая пластинка освещается светом длиной волны 0,2 мкм. Найти напряженность однородного задерживающего поля вне пластинки, если фотоэлектрон может удалиться от нее на расстояние 4 см. Работа выхода электронов из вольфрама 4,5 эВ.
а Пучок электронов движется вдоль оси х со скоростью Положение пылинки m = 0,1 г определено с точностью D x = 10-7 м. Какова неопределенность ее скорости?
Период полураспада изотопа λ=ln2/T1/2 λ= 0,04сут= 4·10-7 Период полураспада радиоактивного аргона 0,75N0=N0e-λt λ= ln2/T1/2=0,006мин λt=ln(4/3) t=ln(4/3) / λ t=47,947мин
i – угол падения, r – угол преломления 6. В дно водоёма глубиной 2,0 м вбита свая, на 0,75 м выступающая из воды. Найти длину тени от сваи на поверхности и на дне водоёма, если высота солнца над горизонтом в данный момент равна 45º. . tg45 = h/l=>l = h/tg45 = h= 0,75 м,
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 888; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.233.71 (0.015 с.) |

 ,
,  , L=rL+l=1,25+0,75=2 м
, L=rL+l=1,25+0,75=2 м Согласно принципу Гюйгенса каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн. Для того чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t+∆t, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени (рис.). Гюйгенс сформулировал его первоначально именно для световых волн. Для механических волн принцип Гюйгенса имеет наглядное истолкование: частицы среды, до которых доходят колебания, в свою очередь, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют. (все точки этого волнового фронта будут являться когерентными источниками сферических вторичных волн, распространяющихся в сторону движения волнового фронта.)
Согласно принципу Гюйгенса каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн. Для того чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t+∆t, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени (рис.). Гюйгенс сформулировал его первоначально именно для световых волн. Для механических волн принцип Гюйгенса имеет наглядное истолкование: частицы среды, до которых доходят колебания, в свою очередь, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют. (все точки этого волнового фронта будут являться когерентными источниками сферических вторичных волн, распространяющихся в сторону движения волнового фронта.) ,
,  ,
, 
 ,
,  ,
, 



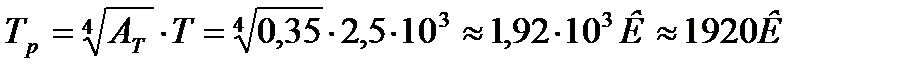
 ; N=
; N=  =
= 


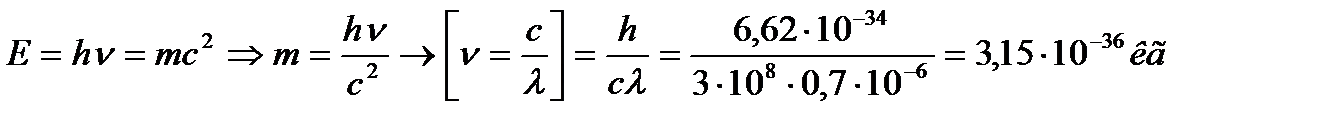
 падает свет с частотой
падает свет с частотой  . Рассчитайте кинетическую энергию выбиваемых из пластины фотоэлектронов.
. Рассчитайте кинетическую энергию выбиваемых из пластины фотоэлектронов. . Найдите работу выхода электронов из калия.
. Найдите работу выхода электронов из калия. ,
, 

 =>
=> 
 , отсюда
, отсюда  , для лития Авых=2,38 эВ.
, для лития Авых=2,38 эВ. , отсюда
, отсюда  ,
, , тогда
, тогда  , длина волны
, длина волны 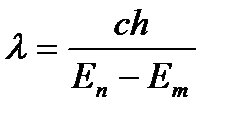
 ?
? или
или  - (1). С другой стороны
- (1). С другой стороны  - (2),
- (2), -длина волны излученного атомом фотона. Приравнивая равные части уравнений (1) и (2). Получаем
-длина волны излученного атомом фотона. Приравнивая равные части уравнений (1) и (2). Получаем  , откуда изменение кинетической энергии электрона
, откуда изменение кинетической энергии электрона 
 .
. =>
=> 
 =
= 




 .
.
 ,
, 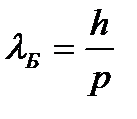 =
= 



 ,
, 
 ,
, 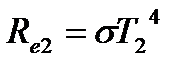 ,
,  ,
, 

 (1). По закону Стефана-Больцмана
(1). По закону Стефана-Больцмана 



 , т.к.
, т.к.  ,
,  ,
, =>
=>  тогда
тогда  . Ответ в В/м или Н/Кл
. Ответ в В/м или Н/Кл , которая определена с точностью 0,01%. Найти неопределенность координаты электрона.
, которая определена с точностью 0,01%. Найти неопределенность координаты электрона.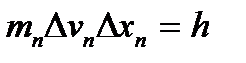 ,
, равен 17,5 суток. Определить постоянную распада этого изотопа.
равен 17,5 суток. Определить постоянную распада этого изотопа. равен 110 мин. Определить время, в течение которого распадается 25 % начального количества атомов.
равен 110 мин. Определить время, в течение которого распадается 25 % начального количества атомов.


