
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон отражения и преломления в электромагнитной теории света.Содержание книги
Поиск на нашем сайте Когда луч достигает плоской границы раздела двух прозрачных сред, он частично проходит во вторую среду (преломляется), частично возвращается обратно (отражается).Закон отражения света был известен еще грекам. Он утверждал, что падающий и отраженный лучи лежат в одной плоскости с нормалью к границе раздела в точке падения (эта плоскость называется плоскостью падения), причем угол падения
Закон преломления был установлен экспериментально в 1621 г. голландским ученым Снеллиусом (1580-1626) и опубликован только после его смерти. Позднее Декарт (1596-1650) в 1637 г. опубликовал тот же закон, не ссылаясь на Снеллиуса. Знал ли Декарт работы Снеллиуса – этот вопрос остался открытым, хотя он и был предметом многочисленных дискуссий. Декарт получил закон преломления Снеллиуса, пользуюсь аналогией между преломлением света и прохождением упругого шара (мяча)через границу раздела воздух с водой. Его рассуждения были неубедительны и крайне туманны, но окончательный результат, к которому он пришел, оказался верным.
Согласно закону преломления Снеллиуса, преломленный луч лежит в плоскости падения, причем отношение синуса угла падения
Постоянная величина Относительный показатель преломления
Это соотношение можно получить путем предельного перехода. Пусть световой луч падает из вакуума на плоскопараллельную пластинку с показателем преломления Для преломления на границах пластинки можно написать Перемножая написанные равенства, получим Это соотношение справедливо, какова бы ни была толщина пластинки. Оно остается верным и в предельном случае, когда толщина пластинки стремится к нулю. Но тогда свет будет преломляться так, как если бы ни какой пластинки вообще не было. Поэтому должно быть Слабая сторона приведенного рассуждения состоит в следующем. Показатель преломления есть макроскопическая характеристика среды. Когда толщина пластинки, разделяющей среды 1 и 2, становится порядка атомных размеров, ее уже нельзя рассматривать как непрерывную среду, так что понятие показателя преломления теряет смысл.Однако окончательный результат (2.5.2) остается верным.Он подтверждается опытом и в дальнейшем при рассмотрении теории отражения и преломления света будет выведен с различных точек зрения. С учетом соотношения (2.5.2) закон преломления можно записать в симметричной форме:
из формулы (2.5.2) следует также:
|
||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |

 равен углу отражения
равен углу отражения  . (рис. 2.5.1)
. (рис. 2.5.1)




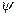 для рассматриваемых сред зависит только от длины световой волны, но не зависит от угла падения, т.е.
для рассматриваемых сред зависит только от длины световой волны, но не зависит от угла падения, т.е.  (2.5.1)
(2.5.1)



 называется относительным показателем или коэффициентом преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем (коэффициентом) преломления этой среды. Его будем обозначать через n, снабжая эту букву если требуется, соответствующими индексами. Например,
называется относительным показателем или коэффициентом преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем (коэффициентом) преломления этой среды. Его будем обозначать через n, снабжая эту букву если требуется, соответствующими индексами. Например,  - показатель преломления первой, а
- показатель преломления первой, а  - второй сред. Ради кратности величину n обычно называют просто показателем (коэффициентом) среды, т.е. опускают прилагательное «абсолютный».
- второй сред. Ради кратности величину n обычно называют просто показателем (коэффициентом) среды, т.е. опускают прилагательное «абсолютный».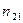 выражается через абсолютные показатели
выражается через абсолютные показатели  (2.5.2)
(2.5.2)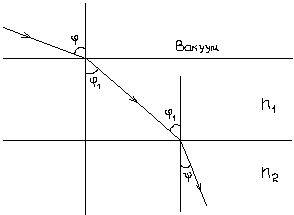
 ,
, 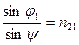
 (2.5.3)
(2.5.3)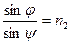 Сравнение этого результата с предыдущим и приводит к соотношению (2.5.2)
Сравнение этого результата с предыдущим и приводит к соотношению (2.5.2) . (2.5.4)
. (2.5.4) . (2.5.5)
. (2.5.5)


