
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сила света по данному направлению определится соотношениемСодержание книги
Поиск на нашем сайте
Охарактеризовав выбранное направление углами широты q и долготы j в некоторой полярной системе координат (рис. 2), можно обозначить силу света по данному направлению через Jq,j. Величина эта есть функция j и q. Из рис. 2 явствует, что
Если J не зависит от j и q (равномерный поток), то из этого общего соотношения следует, что
в согласии с соотношением (1.3). Величина полного светового потока характеризует излучающий источник, и ее нельзя увеличить никакими оптическими системами. Действие этих систем может лишь сводиться к перераспределению светового потока, например, большей концентрации его по некоторым избранным направлениям. Таким способом достигается увеличение силы света по данным направлениям при соответствующем уменьшении ее по другим направлениям. Таково, например, действие сигнальных аппаратов или прожекторов, позволяющих при помощи источников, обладающих средней сферической силой света в несколько сот кандел, создавать на оси прожектора силу света в миллионы кандел. Основной светотехнический эталон есть эталон силы света. 3. Освещенность Е. Освещенностью Е называется величина потока, приходящегося на единицу поверхности: Освещенность площадки s (обозначения те же, что и на рис. 1) есть причем в последних двух равенствах введена сила света J по (1.4) и учтено (1.2). Полученное выражение показывает, что освещенность, создаваемая точечным источником (То есть источником, размеры которого малы по сравнению с расстоянием до освещенной поверхности, и поток от которого равномерен по всем направлениям.), обратно пропорциональна квадрату расстояния от источника до поверхности и прямо пропорциональна косинусу угла, составляемого направлением светового потока (осью узкого конуса, внутри которого распространяется поток) с нормалью к освещаемой поверхности. Это есть основной закон освещенности, создаваемой точечным источником (закон обратных квадратов). Для протяженных источников мы можем разбить поверхность источников на элементарные участки (достаточно малые по сравнению с R ) и, определив освещенность, создаваемую каждым из них по закону обратных квадратов, проинтегрировать затем по всей площади источника, приняв, конечно, во внимание зависимость силы света от направления. Зависимость освещенности от R окажется при этом более сложной. Однако при достаточно больших (по отношению к величине источника) расстояниях можно пользоваться и законом обратных квадратов, т. е. считать источник точечным. Этот упрощенный расчет дает практически хорошие результаты, если линейные размеры источника не превышают
Изменяя при помощи линз и зеркал распределение светового потока, мы получаем возможность сконцентрировать его на определенных участках поверхности и, таким образом, повысить их освещенность, уменьшив одновременно освещенность других. В частности, именно такое назначение имеют всевозможные арматуры (светильники), которыми обычно снабжаются источники света, предназначенные для освещения помещений, рабочих столов, улиц и т. д. Так как в большинстве случаев мы воспринимаем несамосветящиеся предметы, то понятие освещенности приобретает очень важное значение. Большинство проблем светотехники сводится к созданию благоприятной освещенности, В «Нормах освещенности» даются требования, предъявляемые к рациональному освещению рабочих помещений. 4. Яркость источника В. Для многих светотехнических расчетов можно, как мы видели, считать некоторые источники точечными, т. е. пренебрегать их размерами по отношению к расстояниям, на которых наблюдается их действие. Однако многие из этих источников настолько велики, что мы можем при обычных расстояниях наблюдения глазом различить их форму; другими словами, размеры поверхности источника лежат в пределах способности глаза или инструмента отличать протяженный предмет от точки. По отношению к таким источникам, составляющим громадное большинство, имеет смысл определение понятия поверхностной яркости (или просто яркости), неприменимого к источникам, лежащим за пределами разрешающей способности (например к звездам). Поверхностная яркость В есть величина, характеризующая излучение светящейся поверхности по данному направлению, определяемому углом i с нормалью к светящейся поверхности и из данной области поверхности.
Выделим пучок, опирающийся на элемент поверхности s и образующий телесный угол dW; ось пучка составляет угол i с нормалью п к s (рис. 3). Видимая поверхность элемента в направлении оси есть s соs i. Пусть поток, посылаемый ею в телесный угол dW, равен d Ф. Посылаемый поток пропорционален видимой поверхности излучателя s соs i и величине телесного угла dW. Коэффициент пропорциональности зависит от свойств излучающей поверхности и может быть различным для различных направлений углов I относительно нормали. Обозначив этот коэффициент через Bi, найдем
Коэффициент Вi носит название яркости источника по направлению, определяемому углом i. Итак, яркостью в данном направлении называется поток, посылаемый в данном направлении единицей видимой поверхности внутрь единичного телесного угла. Яркость Вi есть величина, зависящая от направления; однако для некоторых источников она может от направления не зависеть. Такие источники называются источниками, подчиняющимися закону Ламберта. Строго говоря, таким источником является только абсолютно черное тело; матированная поверхность или мутная среда, каждый участок которых рассеивает свет равномерно во все стороны, служат более или менее хорошими подобиями ламбертова источника. Такие среды можно назвать идеально рассеивающими, если они подчиняются закону Ламберта. Освещенная поверхность, покрытая окисью магния, или колпак из хорошего молочного стекла, освещенный изнутри, — вот примеры источников, достаточно хорошо приближающихся к ламбертовым. Поверхность Солнца излучает по закону, довольно близкому к закону Ламберта, хотя еще Бугер экспериментально установил, что яркость Солнца несколько падает от центра к периферии, составляя на расстоянии
Рассмотрим светящийся плоский диск S (рис. 4) и светящуюся полусферу S'. Предположим, что обе поверхности подчиняются закону Ламберта и имеют одинаковую яркость В. Тогда световые потоки, посылаемые соответствующими участками диска и сферы по любому направлению, будут одинаковы, ибо видимые поверхности их равны, а яркости по условию не зависят от направления. Таким образом, светящийся диск неотличим от светящейся полусферы, если они подчиняются закону Ламберта. Например, Солнце при не очень тщательных наблюдениях кажется нам плоским диском равномерной яркости; это доказывает, что Солнце является источником, довольно хорошо подчиняющимся закону Ламберта. Знание яркости существенно необходимо при исследовании самосветящихся предметов, в частности, источников света. Наш глаз реагирует непосредственно на яркость источника. Понятие яркости используется и в теории излучения 5. Светимость S.С понятием яркости тесно связано понятие светимости S, представляющей собой интегральную величину, т. е. суммарный поток, посылаемый единицей поверхности наружу по всем направлениям (внутрь телесного угла 2p). Таким образом,
если Ф есть полный поток, посылаемый светящейся площадкой sнаружу по всем направлениям. Светимость и яркость связаны между собой простым соотношением. Поток внутри телесного угла dW по направлению i будет
где j— азимутальный угол. Чтобы получить поток, испускаемый площадкой s, надо это выражение проинтегрировать по всем значениям i и j, определяющим направление внутрь полусферы, т. е. по i от нуля до
Вместе с тем, тот же поток можно выразить через светимость S: Таким образом, связь между светимостью и яркостью выражается соотношением
Для источников, повинующихся закону Ламберта, Вi= В, т. е. не зависит от i. В этом случае имеем
Светимость — очень удобное для многих расчетов понятие. Мы с ним встретимся также в теории излучения. Соотношение освещенность же характеризует освещение поверхности, т. е. поток, приходящий на единицу поверхности. 6. Интенсивность светового потока R. Для характеристики светового поля можно ввести еще понятие интенсивности светового потока. Под интенсивностью понимают величину светового потока, протекающего через единицу видимого сечения по направлению, определяемому углом i между направлением потока и нормалью к этому сечению, внутрь единичного телесного угла: Таким образом, интенсивность светового потока играет для характеристики светового поля ту же роль, что и яркость для характеристики светящейся поверхности. Поэтому ее нередко называют также яркостью светового потока. Из сказанного выше должно быть ясным, что большое количество понятий, связанных с переносимой светом энергией, обусловлено, в конечном итоге, законом прямолинейного распространения света, в силу которого световая энергия может переноситься по-разному в различных направлениях и через элементы поверхности, находящиеся в разных точках. Наиболее дифференцированной характеристикой светового поля служит яркость (или интенсивность), определяющая мощность, распространяющуюся в заданном направлении вблизи заданной точки пространства. Сила света описывает мощность, также распространяющуюся в заданном направлении, но от всей поверхности протяженного источника. Освещенность и светимость характеризуют мощность, которая распространяется вблизи какой-либо определенной точки пространства во всех направлениях. Наконец, наиболее интегральной характеристикой является поток, — мощность, переносимая во всех направлениях через всю заданную поверхность. Приведенные соображения наглядно иллюстрируются соотношениями между введенными величинами и яркостью:
В зависимости от назначения и устройства регистрирующей аппаратуры результаты измерений наиболее естественно выражаются через ту или иную фотометрическую величину. При наблюдении, например, заезд глаз реагирует на свет, испущенный в направлении наблюдателя всей поверхностью звезды; следовательно, в данном случае удобно говорить о силе света звезды. В фотографических приборах неважно, в каком направлении пришел свет в данную точку фотопленки и вызвал ее почернение, т. е. пленка осуществляет интегрирование энергии по углам; поэтому здесь регистрируется освещенность. В приборах с фотоэлектрическими или тепловыми приемниками излучения измеряется, как правило, полный поток, попадающий на всю поверхность приемника по всем направлениям. Единицы измерения введенных фотометрических величин зависят, естественно, от выбора системы единиц. В системе СИ поток измеряется в ваттах, освещенность и светимость — в Вт/м2, сила света — в Вт/ср, яркость и интенсивность — в Вт/(м2ср). Отметим, однако, что в оптических экспериментах сравнительно редко возникает необходимость подсчета потока, проходящего через поверхности с линейными размерами порядка метра. Как правило, речь идет о поверхностях с размерами порядка сантиметра (линзы, зеркала и другие элементы приборов) либо миллиметра (изображение). Поэтому отнесение мощности к м2 неудобно, и в научной литературе часто используются единицы Вт/см2 = 104 Вт/м2 и Вт/мм2 = 106 Вт/м2.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 403; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.72.220 (0.011 с.) |


 (1.4)
(1.4) и, следовательно,
и, следовательно, а полный поток
а полный поток
 (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7) расстояния от источника до освещаемой поверхности. Так, если источником служит равномерно освещенный диск диаметром 50 см, то в точке, лежащей на нормали к центру диска, ошибка в расчете по упрощенной формуле для расстояния 50 см достигает приблизительно 25%, для расстояния 2 м не превышает 1,5%, а для расстояния 5 м составляет всего лишь 0,25%.
расстояния от источника до освещаемой поверхности. Так, если источником служит равномерно освещенный диск диаметром 50 см, то в точке, лежащей на нормали к центру диска, ошибка в расчете по упрощенной формуле для расстояния 50 см достигает приблизительно 25%, для расстояния 2 м не превышает 1,5%, а для расстояния 5 м составляет всего лишь 0,25%.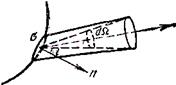
 ИЛИ
ИЛИ  (1.8)
(1.8) радиуса около 80% яркости в центре диска.
радиуса около 80% яркости в центре диска.
 (1.9)
(1.9) так как
так как 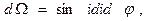
 и по j от нуля до 2p. Итак, полный поток (предполагается независимость Bi от j)
и по j от нуля до 2p. Итак, полный поток (предполагается независимость Bi от j)
 .
. (1.10)
(1.10)
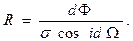 (1.12)
(1.12)





