
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система уравнений Максвелла.Содержание книги
Поиск на нашем сайте
Приведем законы, которым подчиняется поведение электрического и магнитного полей, лежащие в основе теории электромагнетизма. Эти законы, являющиеся обобщением опыта, формулируются ниже в интегральной форме, так как именно в таком виде обычно выражаются данные эксперимента. Используя основные положения векторного анализа, можно записать эти законы электромагнитного поля в дифференциальной форме. Если исследуют электромагнитное поле в каком-либо веществе, изотропно заполняющем пространство, то значение векторов Е и В получаются при усреднении микроскопических величин < Eмикр>=Е и < Hмикр>=В. Такая запись позволяет оперировать с мгновенными напряженностями электрического и магнитного полей в любой точке пространства. Усреднение микроскопических величин законно в том случае, линейные размеры области, где < Eмикр> и< Hмикр> можно считать неизменными,значительно превышают размеры атомов (молеукл). Длина волны При переходе к дифференциальной форме законов электромагнитного поля используют следующие теоремы векторного анализа: Теорема Гаусса о преобразовании поверхностного интеграла в объемный: Теорема Стокса о преобразовании интеграла по замкнутой кривой в поверхностный интеграл (поток ротора через поверхность, охватываемую исследуемой кривой):
Итак, вспомним законы электрического и магнитного полей. Первый из них – основной закон электростатики – закон Кулона. Как следствие этого закона формулируется теорема Гаусса о потоке, которая при наличии диэлектриков в исследуемом пространстве записывается в виде
Отсюда указанным выше способом переходим к дифференциальной форме закона
где D – вектор электрического смещения, Существенно, что выражения (2.3.3) и (2.3.3а), полученные из уравнений электростатики, обобщаются Максвеллом для переменных полей, где D и
Отсутствие в природе магнитных зарядов (монополей) приводит к выражению
которое преобразуется к виду
Эти формулы соответствуют хорошо известным модельным представлением о силовых линиях электрического поля, начинающихся на положительных зарядах и заканчивающихся на отрицательных, тогда как линии магнитного поля замкнуты и охватывают породившие их токи. Введение понятия линий электрического и магнитного полей совершенно не обязательно (смысл законов содержится в приведенных формулах), но, как и во многих случаях, наглядность модельных представлений помогает пониманию явления. Переходя к описанию свойств электрического тока. сформулируем основной закон о зависимости напряженности магнитного поля от силы породившего его тока. Этот закон обычно связывают с именами Био, Савара и Лаплпса. Запишем его в видет, который называют теоремой о циркуляции вектора Н:
Дифференциальная форма этого закона получается применением теоремы Стокса к равенству (2.3.5) и описывает плотности тока j с напряженностью магнитного поля в данной точке:
Как известно, Максвелл ввел ток смещения, плотность которого удовлетворяет соотношению
Ток проводимости и ток смещения дополняют друг друга, образуя полный ток плотностью
которая, согласно Максвеллу, и фигурирует в уравнении (2.3.6) последним из требующихся нам фундаментальных соотношений является математическая формулировка знаменитого открытия Фарадея – закона электромагнитной ин6дукции.
в котором электродвижущая сила При соблюдении некоторых условий эксперимента (в частности, если контур с током неподвижен и не деформируется за время изменений) справедлива следующая интегральная форма записи закона индукции:
откуда легко получается дифференциальная форма закона
Здесь уместно сделать следующее значения: 1.Хорошо известны соображения о вихревом характере электрического поля, порождаемого изменяющимся во времени магнитным полем. Это переменное электрическое поле существенно отличается от потенциального электростатического поля, создаваемого системой неподвижных электрических зарядов, для которого rot E= 0. В последующем нас будет интересовать именно переменное электрическое поле. Но, как было показано Максвеллом, наличие переменного электрического поля с неизбежностью приводит к возникновению связанного с ним магнитного поля и поэтому нужно говорить о едином электромагнитном поле, характеризуемом в каждой точке пространства взаимосвязанными ортогональными векторами Е и В.
2.Введение Максвеллом понятий тока смещения в начале выглядело как гениальная догадка. Но несовместимость сформулированного уравнения электромагнитного поля (2.3.6) и уравнения непрерывности
выражающего одно из самых общих свойств материи – закон сохранения электрического заряда, - с неизбежностью приводит к необходимости введения дополнительного слагаемого в правую часть уравнения поля. Следовательно, уравнение (2.3.6) должно иметь вид
Именно это изменяющееся во времени электрическое поле, столь неудачно названо «током смещения», и связанное с ним магнитное поле будут играть главную роль в дальнейшем изложении. Итак, имеем уравнение электромагнитного поля в следующем виде:
Их нужно дополнить «материальными» уравнениями, учитывающими соотношения между векторами Е, D, В, Н и j. При отсутствии феромагнитных сегнетоэлектрических материалов для изотропных сред можно записать эти уравнения при помощи трех констант: D = Следует также сформулировать граничные условия для уравнений электромагнитного поля, из которых наиболее широко будем использовать равенство тангенциальных составляющих Е и Н на границе раздела двух сред, т.е.
если предположить, что граничащие среды разделены слоем, в котором Система уравнений, включающая в себя уравнения электромагнитного поля, «материальные» соотношения и граничные условия, названа системой уравнений Максвелла и играетв электродинамике ту же роль. что и аксиматика уравнений Ньютона в классической механике.
|
||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.61.176 (0.01 с.) |

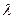 является тем отрезком, на котором напряженность поля сильно изменяется. Поэтому усреднение можно проводить лишь в том случае, когда
является тем отрезком, на котором напряженность поля сильно изменяется. Поэтому усреднение можно проводить лишь в том случае, когда 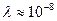 см, т.е. того же порядка что размеры атомов.
см, т.е. того же порядка что размеры атомов.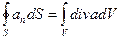 . (2.3.1)
. (2.3.1)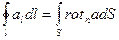 . (2.3.2)
. (2.3.2)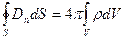 . (2.3.3)
. (2.3.3)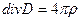 , (2.3.3а)
, (2.3.3а)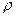 - объемная плотность зарядов.
- объемная плотность зарядов.
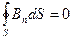 , (2.3.4)
, (2.3.4) (2.3.5)
(2.3.5) (2.3.6)
(2.3.6)
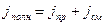 ,
,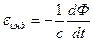 , (2.3.7)
, (2.3.7)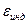 , возникающая в замкнутом контуре, связывается со скоростью изменения потока магнитной индукции Ф, пронизывающего этот контур.
, возникающая в замкнутом контуре, связывается со скоростью изменения потока магнитной индукции Ф, пронизывающего этот контур.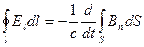 (2.3.8)
(2.3.8)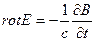 (2.3.9)
(2.3.9)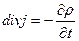 , (2.3.10)
, (2.3.10)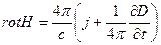 .
.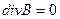 ,
,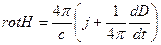 ,
, 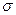 (электропроводность),
(электропроводность), 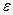 (диэлектрическая проницаемость) и
(диэлектрическая проницаемость) и 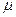 (магнитная проницаемость0, постулируя линейную связь между D и Е, В и Н, j и E, т.е.
(магнитная проницаемость0, постулируя линейную связь между D и Е, В и Н, j и E, т.е.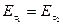 ,
,  (2.3.13)
(2.3.13)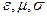 изменяются непрерывно, а j и
изменяются непрерывно, а j и 


